前言:
在前文中,我们探讨了完全二叉树和满二叉树的概念与性质,并基于完全二叉树实现了堆这一数据结构。然而,对于普通二叉树的认识仍有待深入,本文将系统性地介绍普通二叉树的遍历相关内容。

一、前置说明
一般而言,对于一棵普通二叉树是通过链式结构定义,即每个节点包含三个部分:
1.数据域(data):用于存储节点的值
2.左指针(left):用于指向左子节点
3.右指针(right):用于指向右子节点
typedef int BTDataType;//此处将 (int)整形 作为节点存储的内容
typedef struct BinaryTree
{
BTDataType data;
struct BinaryTree* left;
struct BinaryTree* right;
}BTNode;
在学习二叉树的基本操作前,需先要先创建一棵二叉树,然后才能学习其相关的基本操作,但是由于我们对二叉树结构掌握还不够深入,为此我们可以通过手动快速创建一棵简单的二叉树。
如下图所示:

代码实现如下:
BTNode* BuyNode(int x)
{
BTNode* root = (BTNode *)malloc(sizeof(BTNode));
if (root == NULL)
{
perror("malloc fail");
return NULL;
}
root->data = x;
root->left = NULL;
root->right = NULL;
return root;
}
BTNode* TreeCreate()
{
BTNode* node1 = BuyNode(1);
BTNode* node2 = BuyNode(2);
BTNode* node3 = BuyNode(3);
BTNode* node4 = BuyNode(4);
BTNode* node5 = BuyNode(5);
BTNode* node6 = BuyNode(6);
node1->left = node2;
node1->right = node4;
node2->left = node3;
node2->right = node6;
node4->left = node5;
return node1;
}
二、二叉树前序遍历
1. 前序遍历的操作
A、若此棵树为空树,即根节点为NULL,不进行任何操作。
B、若此棵树不为空,即根节点不为NULL,进行如下操作:
①访问根节点
②先序遍历左子树
③先序遍历右节点
所以先序遍历也可简记为: 根 左 右 的顺序进行遍历,具体如何进行遍历,请帅观众耐心往下看。
现在有如下一棵二叉树:
由根节点 -> 左子树 -> 右子树 这个顺序:
那么肯定有帅观众问,直接访问根节点好理解,那么如何理解访问左子树和右子树呢?
其实我们可以把左子树再看成一棵树,这样就又可以看成: 根节点 左子树 右子树
其实我们也可以把右子树也看成一棵树,这样就也可以看成: 根节点 左子树 右子树
如上图所示:根节点1 左子树(以2为根节点) 右子树(以4为根节点)
左子树: 根节点2 左子树(以3为根节点) 右子树(空)
右子树: 根节点4 左子树(以5为根节点) 右子树(以6为根节点)
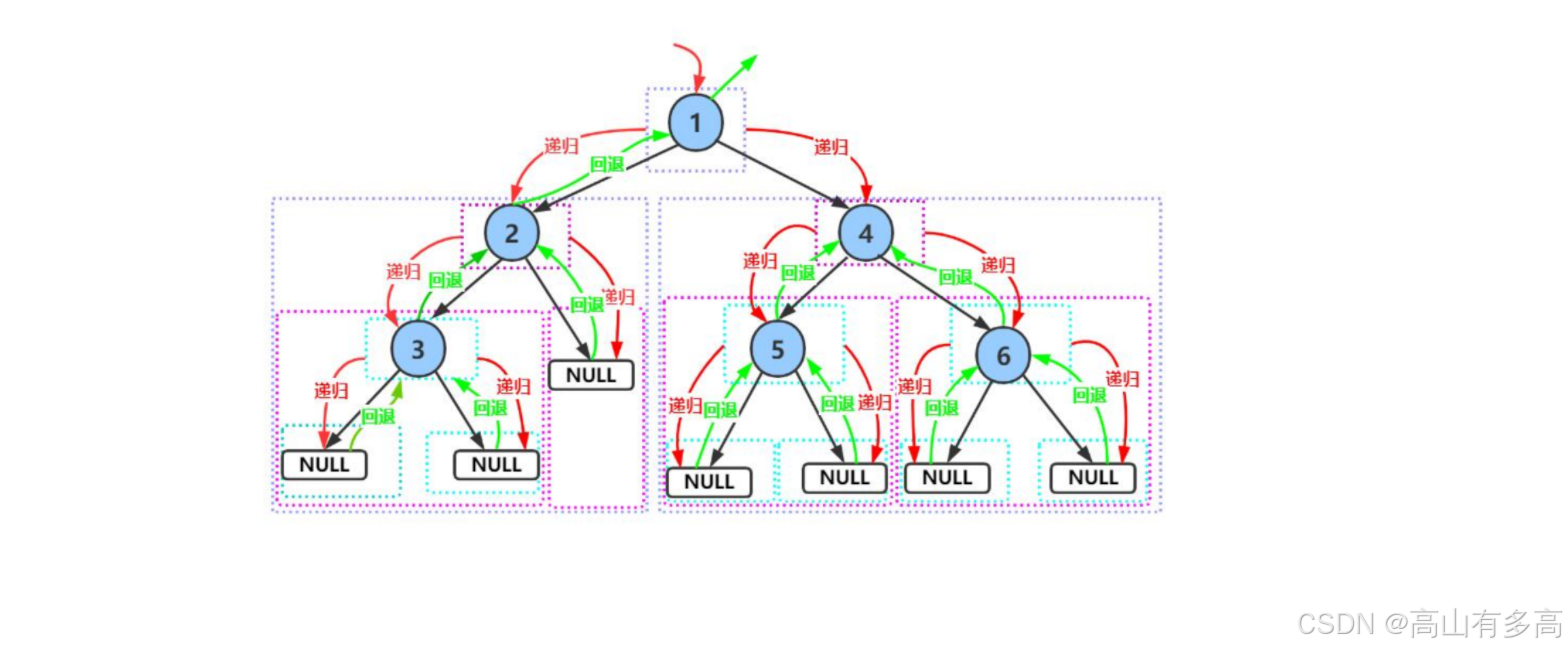
这样是不是将一个大问题分成若干个小问题,这不就是递归的思想,所以我们可以通过递归函数的形式,对先序遍历的代码编写。
前序遍历的结果如下图所示:

如果不省略空节点的打印即为:1 2 3 NULL NULL NULL 4 5 NULL NULL 6 NULL NULL
如果省略空节点的打印即为:1 2 3 4 5 6
2.前序遍历代码实现
//前序遍历
void PrevOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
printf("%d ", root->data);
PrevOrder(root->left);
PrevOrder(root->right);
}
打印结果如下图所示:
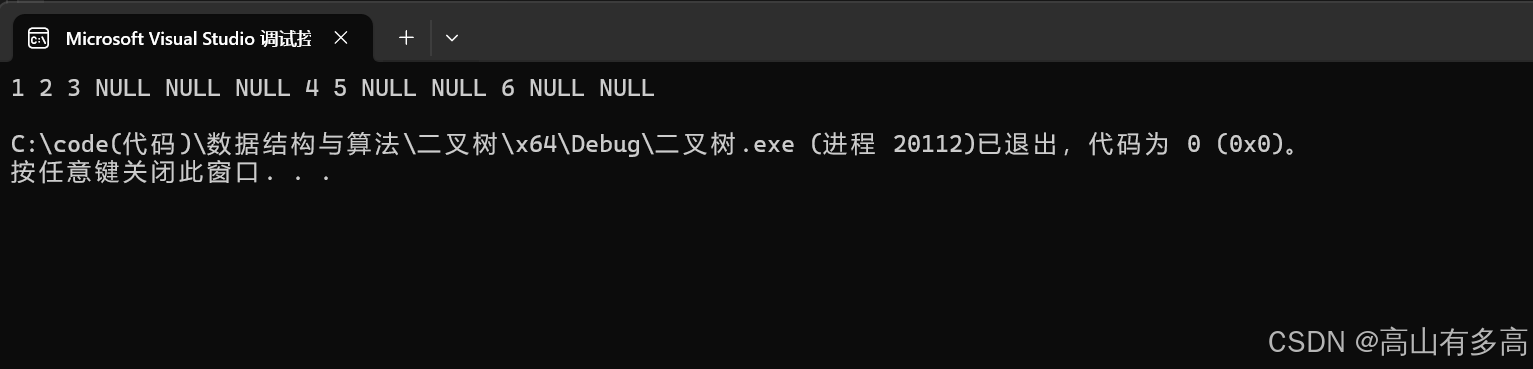
3.递归调用图
三、二叉树中序遍历
1.中序遍历的操作
A、若此棵树为空树,即根节点为NULL,不进行任何操作。
B、若此棵树不为空,即根节点不为NULL,进行如下操作:
①中序访问左子树
②访问根节点
③中序遍历右节点
所以先序遍历也可简记为:左 根 右 的顺序进行遍历。
现有如下一棵二叉树:

中序遍历的结果如下图所示:
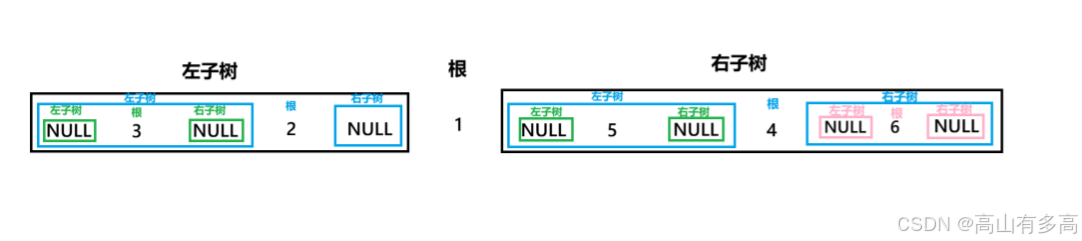
如果不省略空节点的打印即为:NULL 3 NULL 2 NULL 1 NULL 5 NULL 4 NULL 6 NULL
如果省略空节点的打印即为: 3 2 1 5 4 6
2.中序遍历代码实现
//中序遍历
void InOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
InOrder(root->left);
printf("%d ", root->data);
InOrder(root->right);
}

四、二叉树后序遍历
1.后序遍历的操作
A、若此棵树为空树,即根节点为NULL,不进行任何操作。
B、若此棵树不为空,即根节点不为NULL,进行如下操作:
①后序访问左子树
②访问根节点
③后序遍历右节点
所以先序遍历也可简记为:左 右 根 的顺序进行遍历。
现有如下一棵二叉树:

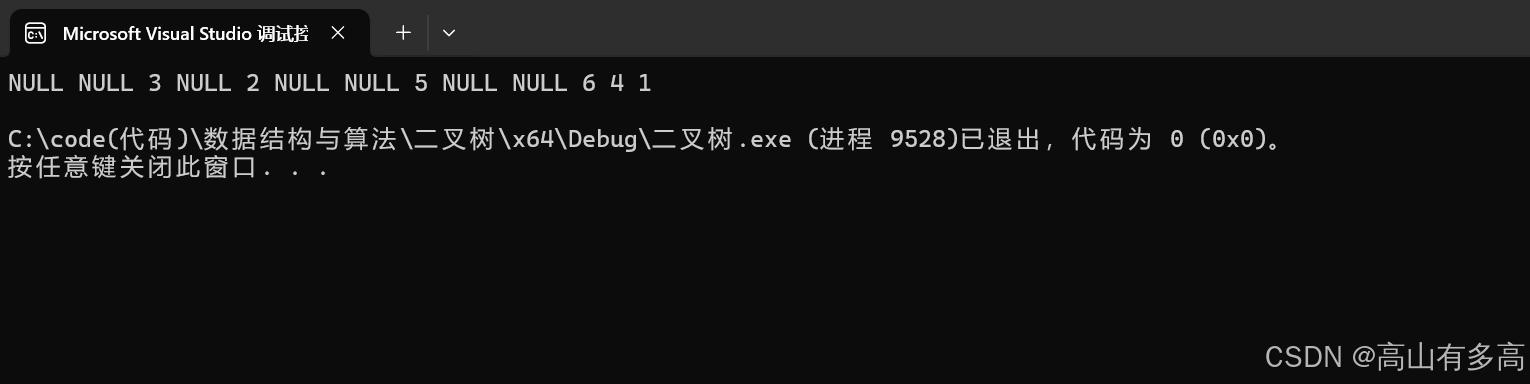
后序遍历的结果如下图所示:
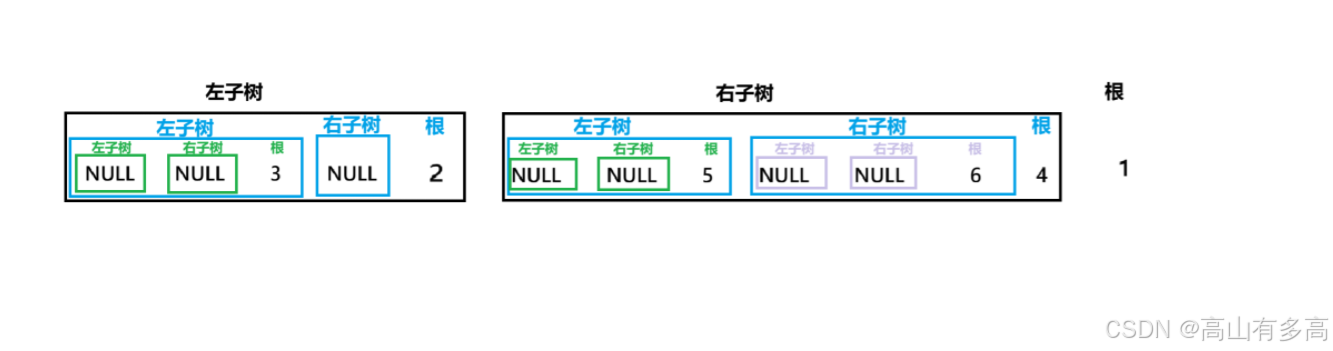
如果不省略空节点的打印即为:NULL NULL 3 NULL 2 NULL NULL 5 NULL NULL 6 4 1
如果省略空节点的打印即为: 3 2 5 6 4 1
2.后序的遍历代码实现
//后序遍历
void PostOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
PostOrder(root->left);
PostOrder(root->right);
printf("%d ", root->data);
}
五、二叉树层序遍历
1.层次遍历的操作
进行层次遍历时需要借助一个队列,层次遍历的核心思想为:上一层的节点出队,带入下一层的节点入队
如下图所示:
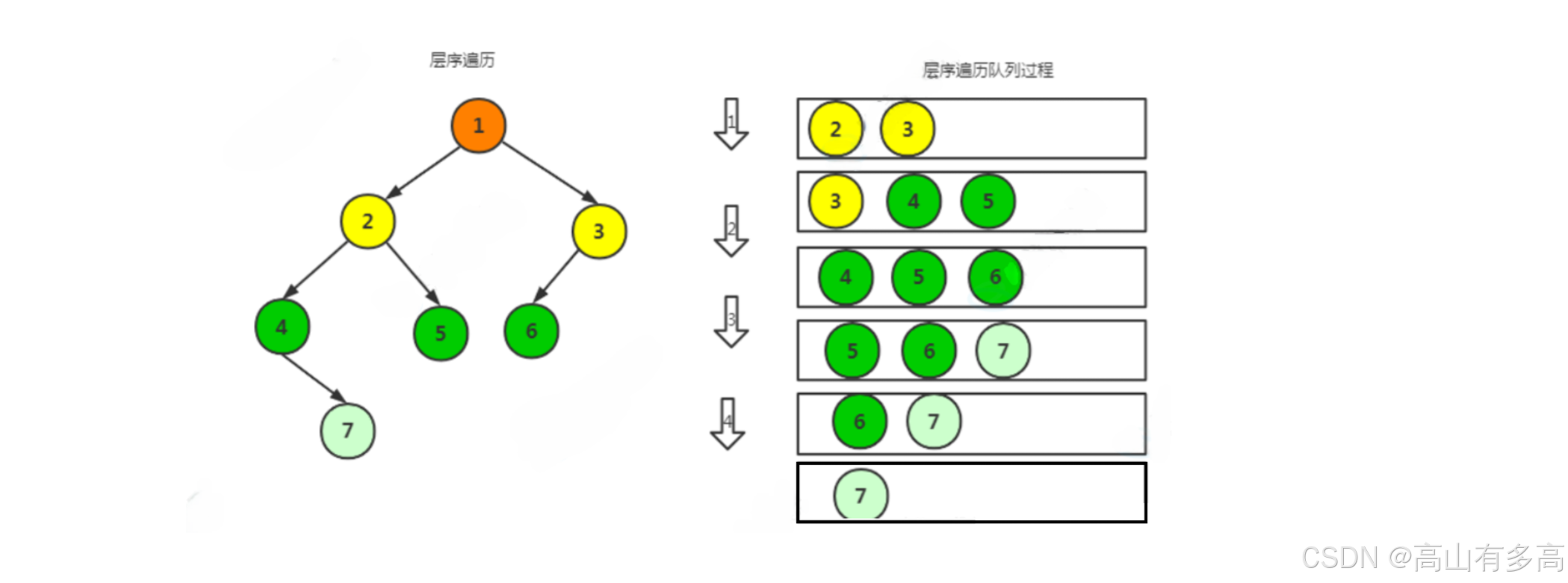
① 将二叉树的根结点入队;
② 若队列非空,则队头结点出队并访问该结点,若它有左孩子,则将其左孩子入队;若它有右孩子,则将其右孩子入队;
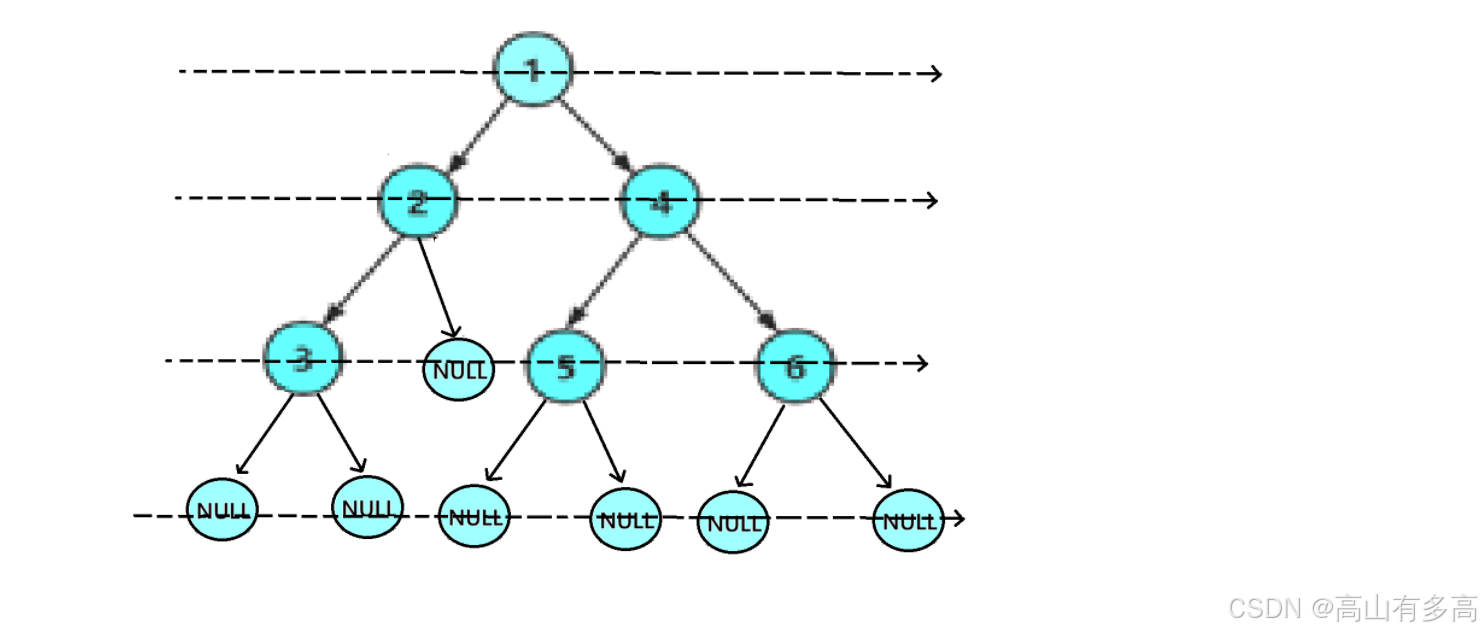
下图为二叉树的层次遍历,即按照箭头所指的方向,按照自上而下,自左向右的顺序对二叉树的各个结点进行逐层访问.
可以得到下图二叉树的层次遍历序列为:1 2 3 4 5 6
2.层序遍历代码实现
// 层序遍历
// 上一层节点出队,带入下一层节点入队
void TreeLevelOrder(BTNode* root)
{
//创建一个队列
Queue q;
//初始化队列
QueueInit(&q);
//如果根节点指针不为空入队
if (root) QueuePush(&q, root);
while (!QueueEmpty(&q))
{
//获取队头元素,获取的是QNode节点中存储的值
BTNode* front = QueueFront(&q);
//出队头,这里是销毁了QNode节点,而存储在QNode节点中的BTNode节点并未删除
QueuePop(&q);
//打印队头信息
printf("%d ", front->data);
//并访问该节点,如果该节点的左孩子存在则入队,如果该节点的右孩子存在则入队
if (front->left) QueuePush(&q, front->left);
if (front->right) QueuePush(&q, front->right);
}
//销毁队列
QueueDestroy(&q);
}
六、小试牛刀
1.练习一
二叉树的前序(先序)遍历为:EFHIGJK,二叉树的中序遍历:HFIEJKG,则二叉树为?
核心思路:由前序遍历确定根,中序遍历确定左右子树
前序遍历的特点:根 左子树 右子树 中序遍历的特点: 左子树 根 右子树
所以对于前序遍历而言,从左往右进行的过程就是相当于对根的遍历
而通过根的确定,对中序序列进行分割左右子树。
二叉树如下图所示:
E / \ F G / \ / H I J \ K
2.练习二
二叉树的中序遍历序列:badce,后序遍历序列:bdeca,则二叉树的形状为?
核心思路:由后序遍历确定根,中序遍历确定左右子树
后序遍历的特点: 左子树 右子树 根 中序遍历的特点: 左子树 根 右子树
对于后序序列从右往左的过程,就相当于对根进行确定
而通过根的确定,对中序序列进行分割左右子树。
二叉树如下图所示:
a / \ b c / \ d e
3.练习三
二叉树的后序遍历序列与中序遍历序列相同,均为 ABCDEF ,则按层次输出(同一层从左到右)的序列
核心思路:由后序遍历确定根,中序遍历确定左右子树
后序遍历的特点: 左子树 右子树 根 中序遍历的特点: 左子树 根 右子树
对于后序序列从右往左的过程,就相当于对根进行确定
而通过根的确定,对中序序列进行分割左右子树。
二叉树如下图所示:
F / E / D / C / B / A故而:层序遍历的结果为:FEDCBA
4.练习四
完全二叉树按层次输出(同一层从左到右)的序列为 ABCDEFGH ,则该完全二叉树的前序序列为?
由层序遍历的特性:自上而下,自左到右
二叉树如下图所示:
A / \ B C / \ / \ D E F G / H故而前序遍历的结果为:ABDHECFG
既然看到这里了,不妨关注+点赞+收藏,感谢大家,若有问题请指正。
























 930
930










