高频二叉树节点问题实战指南

前言：      

        在熟练掌握二叉树四种基本遍历方法的基础上，本文将深入探讨以下进阶问题：节点总数统计、叶子节点计算、第k层节点数量确定、节点的查找以及树高测量。

        这些内容将帮助读者深化对二叉树结构的理解与应用能力，以及深入理解递归分治思想。

 

        

一、前置说明：

        

本文所描述的二叉树都是链式二叉树，其定义方式如下所示：

        

typedef char BTDataType;

typedef struct BinaryTree
{
	BTDataType data;
	struct BinaryTree* left;
	struct BinaryTree* right;
}BTNode;

        

二、二叉树的创建及销毁

        

通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树，其中'#'表示该节点为NULL，二叉树如下图所示：

        

        

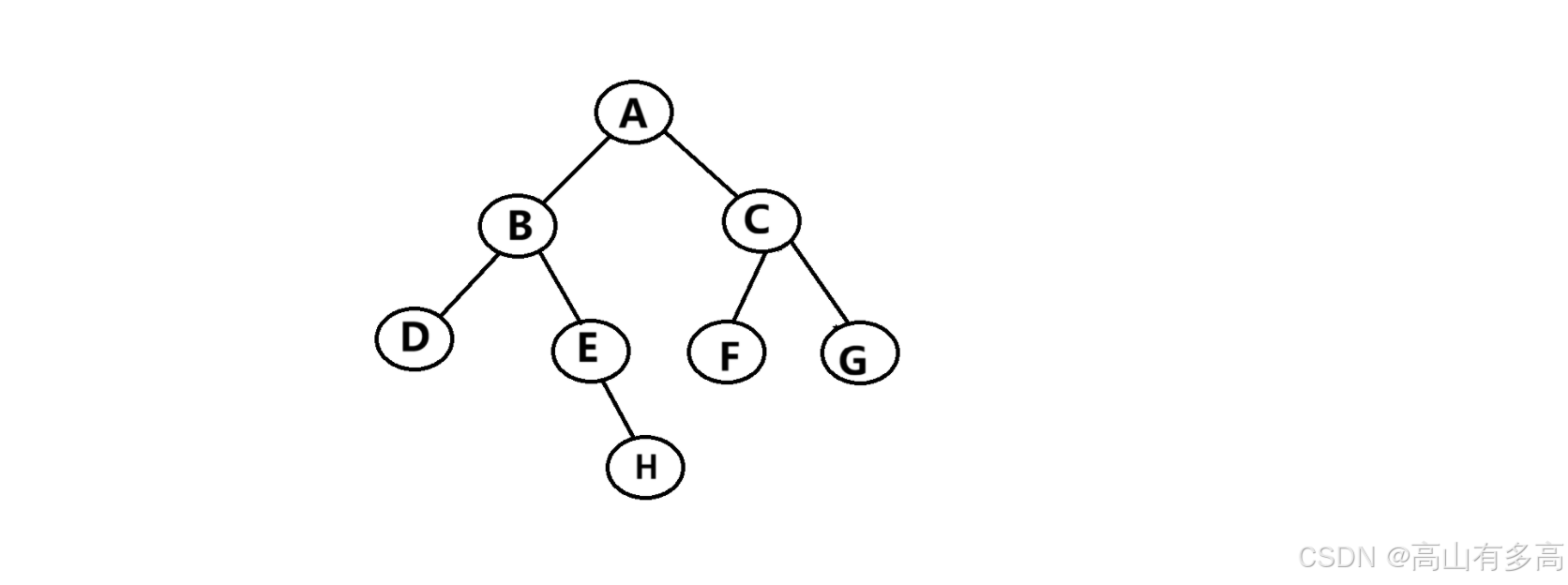
前序遍历的思想为： 先访问根节点  ->  再访问左子树 ->  最后访问右子树

        

依照前序遍历的思想，我们可以得出核心构建二叉树的逻辑：“先处理当前节点，再递归构建左子树，最后递归构建右子树 ”。

      

BTNode* BinaryTreeCreate(char* a, int n, int* pi)
{	

	if (a[*pi] == '#')
	{
		(*pi)++;
		return NULL;
	}

	BTNode* root = (BTNode*)malloc(sizeof(BTNode));
	root->data = a[(*pi)++];

	root->left = BinaryTreeCreate(a, n, pi);
	root->right = BinaryTreeCreate(a, n, pi);

	return root;
}

        

核心逻辑：整个递归从根节点 A 开始，按 “当前节点→左子树→右子树” 的前序逻辑推进

          

①先取 A 为节点，递归构建其左子树（以 B 为节点）。

        

②B 节点下先递归构建左子树（D 节点，左右均为 #则返回），再构建右子树（E 节点，左为 #，右递归到 H 节点，H 左右均为 #则返回）。

        

③A 的右子树以 C 为节点，递归构建左子树（F 节点，左右均为 #返回）和右子树（G 节点，左右均为 #返回），遇 #则终止当前分支递归，逐层完成构建。

        

对于二叉树的销毁而言，我们需要按照后序遍历的思想：先访问左子树  ->  再访问右子树 ->  最后访问根节点

这里有帅观众问，为什么一定需要按照后序的遍历思想？

答：若按照前序遍历 或者 中序遍历的思想，根节点会提前释放，导致左子树和右子树所开辟的空间不能被释放，造成内存泄漏的严重后果。

        

依照后序遍历的思想，我们可以得出销毁二叉树的逻辑：“先递归处理左子树，再递归处理右子树，最后销毁根节点 ”。

        

void TreeDestory(BTNode** root)
{
	if (*root == NULL) return;

	//销毁左树
	TreeDestory((*root)->left);

	//销毁右树
	TreeDestory((*root)->right);

	//销毁根
	free(*root);
	*root = NULL;
}

        

        

三、二叉树的结点统计与高度计算

        

温馨提示：下文中对如图所示的二叉树进行节点与高度的计算

        

        

3.1二叉树节点总数的统计

        

思路一： 通过定义计数变量，通过遍历整棵二叉树进行统计节点个数。

        

思路二：利用分治思想，结合递归函数，将大问题化成若干个子问题。

                整棵树的结点总数 = 左子树结点数 + 右子树结点数 + 1（根结点），空树结点数为 0。

思路一看似很合理，但实际上会出现问题

             

具体问题如下：

        

①若使用局部变量：

        

递归遍历左 / 右子树时，每层递归的局部计数变量会被重新初始化，无法累计整棵树的节点数

        

②若使用全局 / 类成员变量：

        

虽然能累计计数，但多次调用统计函数时，全局变量不会自动重置，会导致后续统计结果错误。

        

例如：统计了A树的节点个数，再统计B树的节点个数就会因没重置计数变量，而导致统计结果错误。

        

下面基于思路二的思想进行代码展示：

//树的节点个数
int TreeSize(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	return TreeSize(root->left) + TreeSize(root->right) + 1;
}

        

3.2叶子节点的计算

        

思路：①由叶子结点是 “左、右子树均为空” 的结点，得出判断条件

           ②由分治思想，将大问题化成若干个子问题，整棵树的叶子结点数 = 左子树叶子结点数 + 右子树叶子结点数。

        

//叶子节点个数
int TreeLeafSize(BTNode* root)
{
    //若根节点为空，直接返回0
	if (root == NULL)
	{
		return 0;
	}
	if (root->left == NULL && root->right == NULL)
	{
		return 1;
	}
	return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}

        

3.3第k层节点的数量

        

思路：①由分治思想，将大问题化成若干个子问题，第k层节点数 = 左子树的第k-1层节点数 + 右子树的第k-1层节点数。

            ②明确最小子问题：若树为空（根节点null）或k < 1 → 第k层节点数为0；   若k = 1 → 只有根节点，数量为1；

        

int TreeLevelKSize(BTNode* root, int k)
{
	//第k层 的节点数 ->第k-1层的节点数 ->第k-1层左子树+第k-1层右子树的节点数

	if (root == NULL|| k<0) return 0;
    
	//第一层的节点数为1
	if (k == 1) return 1;

	return  TreeLevelKSize(root->left, k - 1) + TreeLevelKSize(root->right, k - 1);
}

        

3.4二叉树的高度测量

        

思路：由分治思想，将大问题化成若干个子问题，二叉树的高度=max( 左子树 , 右子树 ）+ 1

写法一:             

//树的高度
int TreeHeight(BTNode* root)
{
	if (root == NULL)
		return 0;
    
    return max(TreeHeight(root->left),TreeHeight(root->right))+1;
}

        

写法二：

//树的高度
int TreeHeight(BTNode* root)
{
	if (root == NULL)
		return 0;

	int leftHeight = TreeHeight(root->left);
	int rightHeight = TreeHeight(root->right);

	return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
}

        

错误写法：因为没有记录左右子树的高度，导致需要进行多次重复冗余的递归，使得增加栈溢出的风险。

//树的高度
int TreeHeight(BTNode* root)
{
	if (root == NULL)
		return 0;

	return TreeHeight(root->left) > TreeHeight(root->right) ? TreeHeight(root->left) + 1 : TreeHeight(root->right) + 1;
}

        

3.5节点的查找

        

思路：  ①由分治思想，将大问题化成若干个子问题，将在整棵树查找节点-> 根查找   左子树查找   右子树查找

             ②边界条件：遇到空子树返回NULL，遇到值等于查找目标返回该节点。

             ③温馨提示：在查找到目标节点需要进行保存后，逐层返回。

BTNode* TreeFind(BTNode* root, BTDataType x)
{
    //查找到空节点直接返回
	if (root == NULL) return NULL;
    
    //查找到目标节点的判定
	if (root->data == x) return root;

	BTNode* retleft = TreeFind(root->left, x);
	//在左子树找到，保存并直接返回
	if (retleft) return retleft;

	BTNode* retright = TreeFind(root->right, x);
	//在右子树找到，保存并直接返回
	if (retright) return retright;

	//左右子树都没找到
	return NULL;
}

        

3.6测试函数功能        

        

void TestFun()
{
    char a[] = "ABD##E#H##CF##G##";
    int sz = sizeof(a) / sizeof(char);
    int i = 0;
    BTNode* root = BinaryTreeCreate(a, sz, &i);

    // 测试各功能
    printf("节点总数为：%d\n", TreeSize(root));          // 预期8
    printf("叶子节点数为：%d\n", TreeLeafSize(root));   // 预期4（D、H、F、G）
    printf("树的高度为：%d\n", TreeHeight(root));       // 预期4（A→B→E→H）
    printf("第3层的节点数：%d\n", TreeLevelKSize(root, 3)); // 预期4（D、E、F、G）

    // 测试查找功能
    BTNode* findNode = TreeFind(root, 'H');
    if (findNode)
	{
		printf("找到节点：%c\n", findNode->data);
	}
	else 
    {
		printf("未找到节点\n");
	}

    // 销毁二叉树
    BinaryTreeDestroy(root);
    root = NULL;
}

既然看到这里了，不妨关注+点赞+收藏，感谢大家，若有问题请指正。