运筹学那些事，专科学生学习运筹学之线性规划，No.4

线性规划

概述

重点概念提炼

• “规划” 就是使用某种数学方法使有效资源的运用达到最优化。
• 规划就是计算，以数学形式表达的一定条件下的一组方程式和/或一组不等式中求某些未知量。

线性规划的模型结构

线性规划的定义：线性规划是求一组变量的值，在满足一组约束条件下，求得目标函数的最优解，使决策目标达到最优，

线性规划模型的基本结构包含如下内容

1. 变量（也叫决策变量）
2. 目标函数（线性规划一般只解决单目标问题）
3. 约束条件
4. 线性规划的变量应为正值

线性规划建立模型时的四个步骤

1. 明确问题，确定目标，列出约束因素
2. 收集资料，确立模型
3. 模型求解与检验
4. 优化后分析

教材中提供了一个说明线性规划基本结构和建模基本步骤的案例

例题：设某家具厂生产桌子和碗橱两种产品，分别由加工、装配、油漆三个工段完成。相关数据如下

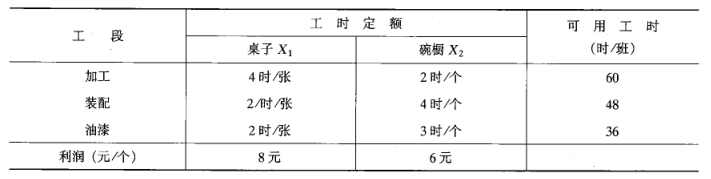
要求：在不超出三个工段的可用工时的情况下，合理搭配品种（桌子、碗橱），使得每班获得利润最