洛谷P3367【模版】并查集 C++题解

呃，之前一直没有多么了解过并查集，刚刚学习了一下。现在发个模版题解，可能有错误，望指正！(⁎˃ᴗ˂⁎)

如有雷同，纯属巧合

一、题目详情

>传送门<

二、并查集是什么

并查集( $DSU$ ),是一个支持合并和查询的集合，
并查集的名字便是从他的用途中得出的。

我们用一个现实例子来讲解并查集：

两个人有熟不熟的关系，假如 $ABCD$ 几个人互相熟悉，我们就成他们是一个小团体，也就是一个集合。每个小团体都有一个"领导"，这是我们假设出来的，便于我们操作，实际上所有元素都是平等的。

我们会用并查集的两个操作来操作人们的关系，两个操作在后面可见。

三、并查集的操作

初始化

初始化时，大家都不熟悉，也就是每个人都是"领导"。在并查集中，父节点是自己的就是领导。

这是初始化的代码，我们直接把它做成 init() 函数：

// 初始化 
void init(){
	for (int i = 1;i <= n;i++){
		fa[i] = i; //这里的 fa[i] 指的是 i 的父节点
		// 一开始的时候,每个人自己是一个小团体，领袖就是自己
	}
}

用图来表示一下此时的状态：

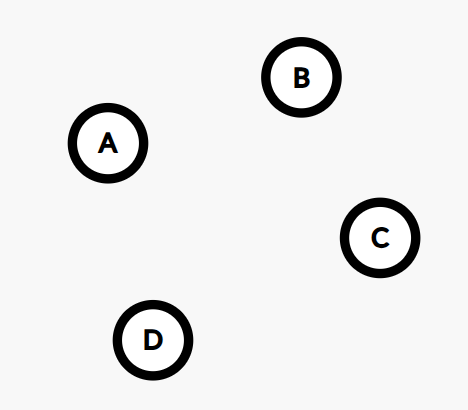
查询"领导"

查询操作是通过父节点为基础进行的，通过不断向上查找父节点的父节点得到"领导"。

以此图为例，从 $C$ 点来查"领导"的操作是这样的：

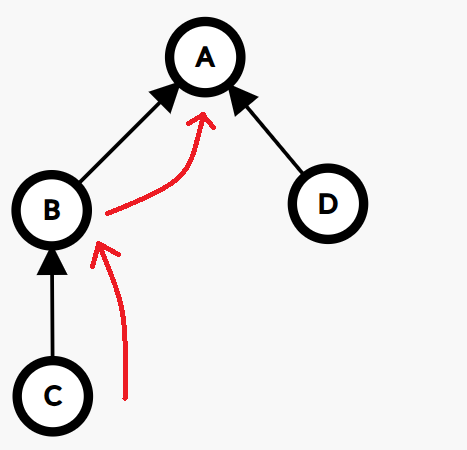
于是我们能得到这样的代码，将它做成 find() 函数：

// 查询 x 的领导 
int find(int x){
	if (fa[x] == x) return x; // 如果自己的上级是自己,说明找到了领导
	else return find(fa[x]);  // 还没找完,继续向上找
}

当然，在P3367中，用这种方法包会超时的(当然，这个是为了效果故意做的…)：

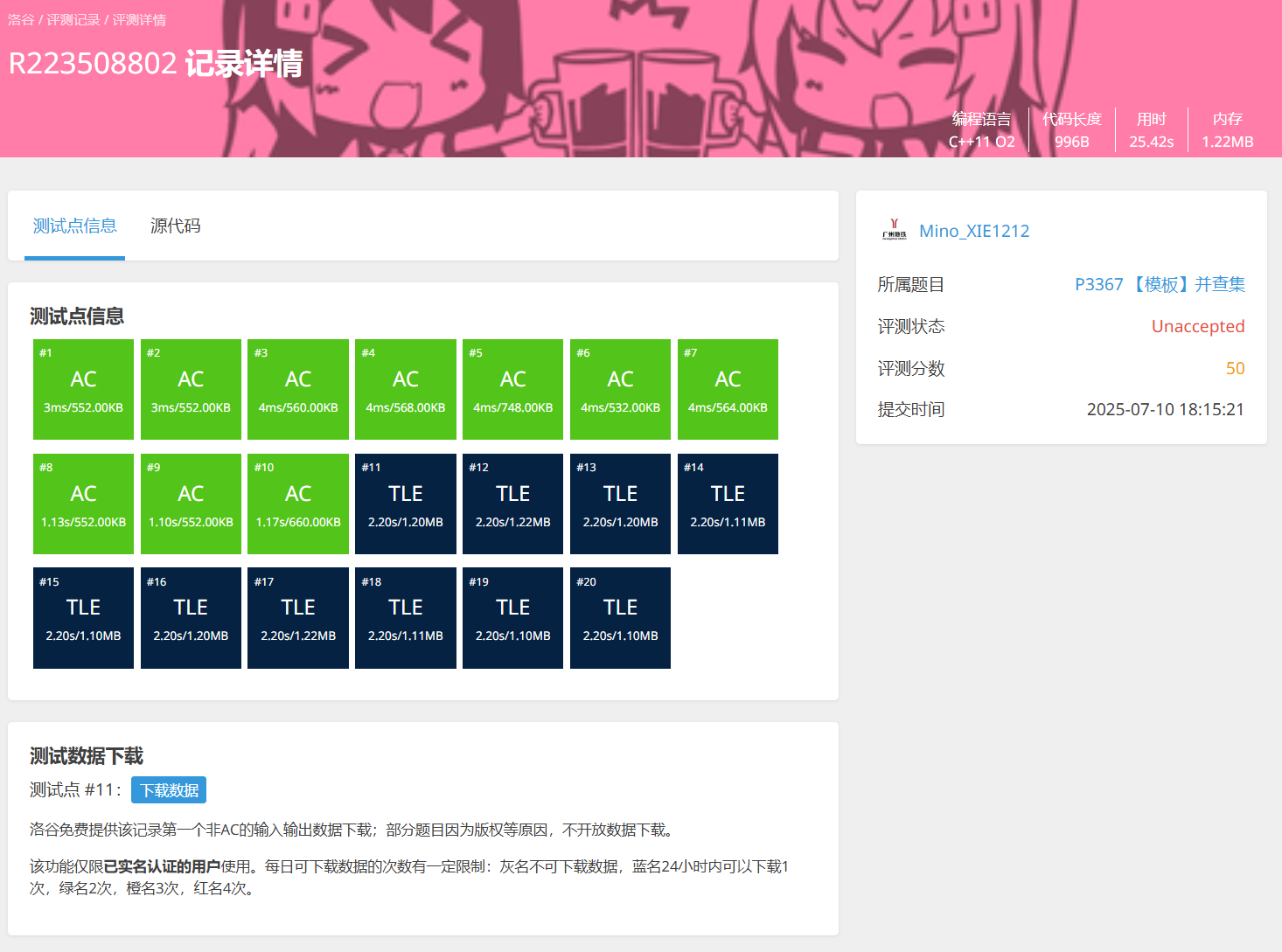
解决方法是路径压缩优化！只需要把每一个经过的点直接连接到"领导"上就可以了。

这是升级版代码:

// 查询 x 的领导 
int find(int x){
	if (fa[x] == x) return x; // 如果自己的上级是自己,说明找到了领导
	else return fa[x] = find(fa[x]); // 还没找完,继续向上找
	// find 的第二行用了优化,他直接将路过的节点连接到了领导 
}

合并集合

合并就非常简单了，我们可以把 $x$ 或 $y$ 中的一个人的父节点设为 $y$ 的 领导或 $x$的领导。如图所示：

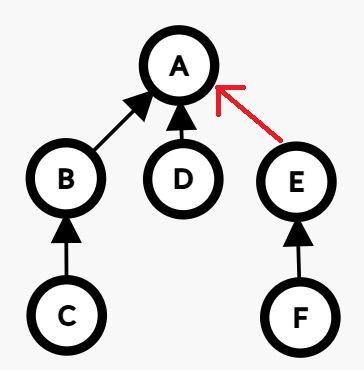
代码可以做成 merge() 函数：

// 合并 
void merge(int x,int y){
	x = find(x),y = find(y); // 查询自己领导
	if (x == y) return ; // 如果在同一个集合中,直接不合并
	else fa[x] = y; // fa[y] = x也可以
	// merge 的第三行代码写出把 x 的领导连接到 y 的领导上,代表合并两个集合 
}

这样子，就可以通过代码了，但是有更加快速的秩优化。

按秩合并优化，英文名为rank，但中文的翻译很奇怪。它主要防止树的深度增加，让树的深度达到最小，让操作更加快速。我们只用设一个 rank[] 数组，用作记录秩，并在合并时比较他即可。

秩优化后代码：

x = find(x),y = find(y); // 查询自己领导
	if(x == y) return ; // 如果在同一个集合中,直接不合并
	if(Rank[y] < Rank[x]) swap(x,y); // 改变合并顺序
	if(Rank[x] == Rank[y]) Rank[y] = Rank[x]+1; // 计算新的秩：如果两个集合的秩相等，那么秩加一
	fa[x] = y; // 合并 

四、总结

这道题就做完了：

#include<bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10;
#define I return
#define AK 0
#define IOI ;
#define qio ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
int fa[N]; // fa 数组指出了 i 的上级
int n,m;
int Rank[N];
// 初始化 
void init(){
	for (int i = 1;i <= n;i++){
		fa[i] = i;
		// 一开始的时候,每个人自己是一个小团体，领袖就是自己
	}
}
// 查询 x 的领导 
int find(int x){
	if (fa[x] == x) return x; // 如果自己的上级是自己,说明找到了领导
	else return fa[x] = find(fa[x]); // 还没找完,继续向上找
	// find 的第二行用了优化,他直接将路过的节点连接到了领导 
}
// 合并 
void merge(int x,int y){
	x = find(x),y = find(y); // 查询自己领导
	if(x == y) return ; // 如果在同一个集合中,直接不合并
	if(Rank[y] < Rank[x]) swap(x,y); // 改变合并顺序
	if(Rank[x] == Rank[y]) Rank[y] = Rank[x]+1; // 计算新的秩：如果两个集合的秩相等，那么秩加一
	// 否则秩不变 
	fa[x] = y; // 合并 
}
int main(){
	qio
	cin >> n >> m;
	init();
	for (int i = 1;i <= m;i++){
		int opt,x,y;
		cin >> opt >> x >> y;
		if (opt == 1){
			merge(x,y);
		}
		else{
			x = find(x),y = find(y);
			if (x == y) cout << "Y" <<endl;
			else cout << "N" <<endl;
		}
	}

	I AK IOI
}
/*Notes:=================

=======================*/
//Coder:Mino_XIE1212

麻烦点个关注吧~