快速幂取模的迭代方法

最新推荐文章于 2024-11-18 15:59:13 发布

原创最新推荐文章于 2024-11-18 15:59:13 发布 · 270 阅读

CC 4.0 BY-SA版权

文章标签：

#include <stdio.h>

typedef long long LL;

LL pow(LL a, LL b, LL m){
    LL ans = 1;

    for(int i = 0; i < b; i++){
        ans = ans * a % m;
    }

    return ans;
}

int BinaryPow(int a, int b, int m){
    if(b == 0) return 1;
    if(b & 1){
        return a * BinaryPow(a, b - 1, m) % m;
    }
    else{
        int mul = BinaryPow(a, b / 2, m);
        return mul * mul % m;
    }
}
LL BinaryPow1(LL a, LL b, LL m){
    LL ans = 1;
    while(b){
        if(b & 1) ans = ans * a % m;
        a = a * a % m;
//        a *= a;
        b >>= 1;
    }

    return ans;
}

LL BinaryPow2(LL a, LL b, LL m){
    LL ans = 1;
    while(b){
        if(b & 1) ans = ans * a % m;
        a *= a;
        b >>= 1;
    }

    return ans;
}

int main()
{
    LL a, b, m;

    while(scanf("%I64d%I64d%I64d", &a, &b, &m) != EOF){

    printf("%I64d\n", BinaryPow1(a, b, m));
    printf("%I64d\n", BinaryPow2(a, b, m));
    }

    return 0;
}

迭代方法中，函数BinaryPow1与BinaryPow2的不同之处在于a由
a ^ (2^k)
到a ^ (2^(k + 1))时，前者为a = a * a % m;后者为a = a * a;
在数学意义上两个函数都能得到正确的结果，因为 a^4 % m
= (a^2 * a ^2) % m = (a^2 % m * a ^2 % m) % m。但是当a过大时， a ^ 2会超出long long 的范围，结果就错误了。
验证如图：
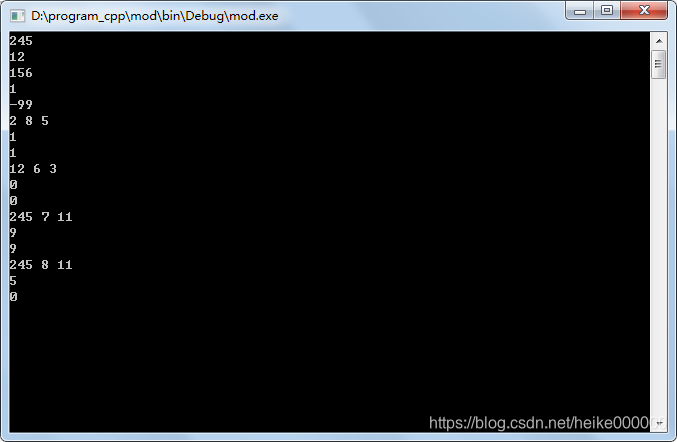
在这里插入图片描述
其中245 ^ 7 = 5.299*10^16,未溢出，两个函数结果相同。(longlong 正数最大为2 ^ 63 -1,约为9 * 10 ^18).
245^8 = 1.298 * 10^19,溢出，于是第二个函数得到了错误的结果。