斜率公式解释说明及示例

斜率公式用于确定直线的陡度或倾角。直线上各点的 x 和 y 坐标用于计算直线的斜率。y 坐标相对于 x 坐标变化的变化称为直线的斜率，通常用字母“m”表示。

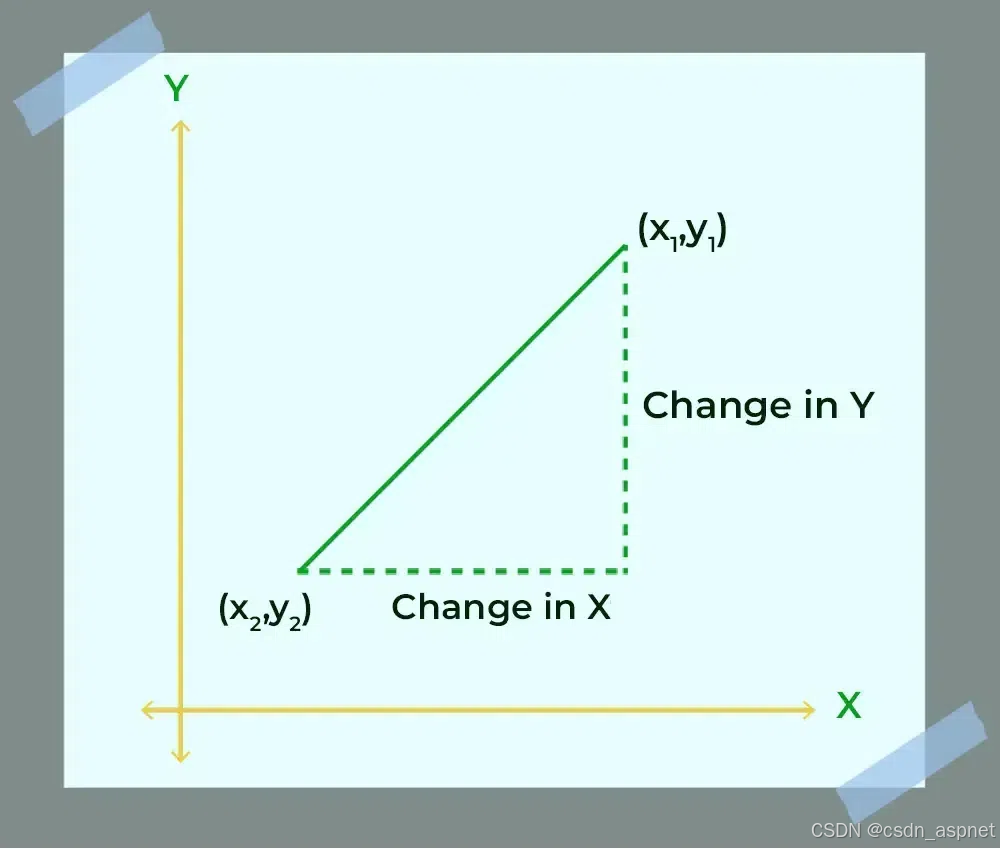
计算直线的倾角需要斜率公式。计算直线的斜率需要直线上点的 x 和 y 坐标。y 坐标的变化量与 x 坐标的变化量之比称为直线的斜率。

如果您喜欢此文章，请收藏、点赞、评论，谢谢，祝您快乐每一天。 

斜率（m）= y 的变化/x 的变化 = Δy/Δx 
公式英文：【Slope (m) = change in y/change in x = Δy/Δx】

在数学中，直线的斜率用于确定直线倾斜的程度，即直线的陡度。

要确定直线的斜率，我们需要直线上点的 x 和 y 坐标。斜率公式是 y 坐标的净变化量除以 x 坐标的净变化量。Δy 是 y 坐标的变化量，Δx 是 x 坐标的变化量。因此，y 坐标的变化量与 x 坐标的变化量之比为：

斜率（m）= y 的变化/x 的变化 = Δy/Δx

m= (y 2 - y 1 )/(x 2 - x 1 )

公式英文：
【Slope (m) = change in y/change in x = Δy/Δx

m= (y2 - y1)/(x2 - x1)】

在哪里

• x 1和 x 2是 X 轴的坐标
• y 1和 y 2是 Y 轴的坐标

斜率公式的推导

直线的 x 和 y 坐标用于计算斜率。y 坐标的净变化量为 Δy，x 坐标的净变化量为 Δx。因此，y 坐标相对于 x 坐标变化量的变化可以写成：

m = Δy/Δx

在哪里，

• m是斜率
• Δy是 y 坐标的变化
• Δx是 x 坐标的变化

我们知道 tanθ 也是直线的斜率，其中 θ 是直线与 x 轴正方向的夹角。

并且，tanθ=高/底，公式英文：【tan θ = height/base】

因为任意两点之间的高/底 = (y 2 - y 1 )/(x 2 - x 1 )

因此，斜率方程为 m = tan θ = Δy/Δx

从图中我们观察到：

Δy = (y 2 - y 1 )

Δx = (x 2 - x 1 )

然后，斜率公式如下：

斜率 = m = (y 2 - y 1 )/(x 2 - x 1 )

公式英文：【Slope = m = (y2 - y1)/(x2 - x1)】

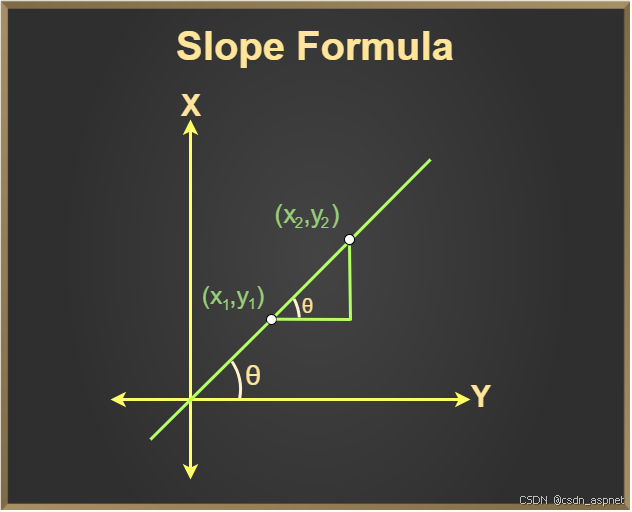
直线斜率公式

• 我们知道tanθ也是直线的斜率，因此直线的斜率也可以表示为，
斜率（m）= tanθ = Δy/Δx

公式英文：【Slope (m) = tan θ = Δy/Δx】

其中θ是直线与正 X 轴的夹角，

• Δy =“y”坐标的变化，
• Δx =“x”坐标的变化。

• 我们还可以将直线的斜率定义为上升长度与运行长度的比率。

坡度（米）= 上升/下降

公式英文：【Slope (m) = Rise/Run】 

• 设 ax + by + c = 0 为直线的通式。则直线斜率的公式为：

斜率 (m) = - x 系数 / y 系数 = -a/b

公式英文：【Slope (m) = - coefficient of x / coefficient of y = -a/b】

• 使用直线方程的直线斜率截距形式如下，
y = mx + c

其中m是直线的斜率，c 是直线的 y 截距。

斜率方程

斜率公式用于确定直线的斜率。用于计算斜率的公式如下：

m = tanθ = Δy/Δx = (y 2 - y 1 )/(x 2 - x 1 )

在哪里，

• m是直线的斜率
• Δy是 y 坐标的差值
• Δx是 x 坐标的差值
• θ是直线与 x 轴正方向的夹角

斜率为 m 的直线方程为：

y = mx + c

在哪里，

• m是直线的斜率
• b是直线的 y 截距

斜率公式示例

例 1：求坐标为 (3, 7) 和 (5, 8) 的直线的斜率。

解决方案：

给定 (x 1 , y 1 ) = (3,7) 和 (x 2 , y 2 ) = (5,8)

斜率公式 (m) = (y 2 - y 1 )/(x 2 - x 1 )

⇒ m = (8 - 7)/(5 - 3) = 1/2

因此，给定线的斜率为 1/2。

例 2：确定坐标为 (7, -5) 和 (2, -3) 的直线的斜率。

解决方案：

给定，（x 1， y 1）=（7，-5）和（x 2， y 2）=（2，-3）

斜率公式 (m) = (y 2 - y 1 )/(x 2 - x 1 )

⇒ m = (-3 - (-5))/(2 - 7) = -2/5

因此，给定线的斜率为 -2/5

例 3：如果通过点 (-4, a) 和 (2, 5) 的直线的斜率为 3，则求 a 的值。

解决方案：

已知 (x 1 , y 1 ) = (4,a) 和 (x 2 , y 2 ) = (2, 5) 且斜率 (m) = 3

我们知道斜率 (m) = (y 2 - y 1 )/(x 2 - x 1 )

⇒ 3 = (5 - a)/(2 - 4)

⇒ 3 = (5 - a)/(-2)

⇒ -6 = 5 - a ⇒ a = 5 + 6 = 11

因此，a 的值 = 11

例 4：如果一条线与 Y 轴正方向成 60° 角，那么该线的斜率是多少？

解决方案：

给定数据，一条线与正 y 轴的夹角 = 60°

我们知道，如果该线与正 y 轴成 60° 角，那么它与 x 轴成 (90° - 60° = 30°) 角。 

因此，直线斜率的值 (m) = tan 30° = 1/√3

因此，直线斜率的值 = 1/√3。

例5：Sheela正在查看一张图表，她注意到加息幅度为12个单位，减息幅度为4个单位。现在计算直线的斜率。

解决方案：

给定数据，上升 = 12 个单位，运行 = 4 个单位

我们知道坡度（m）=上升/下降

⇒ m = 12/4 = 3

因此，给定直线的斜率为 3

例 6：求直线 3x - 7y + 8 = 0 的斜率。

解决方案：

给定数据，直线方程 = 3x - 7y + 8 = 0

现在，将给定的与直线的一般方程进行比较，即 ax + by + c = 0

因此，a = 3，b = -7，c = 8

我们知道斜率（m）= - x 系数/y 系数 = -a/b

⇒ m = -3/(-7) = 3/7

因此，给定线的斜率为 3/7。

斜率公式练习题

Q1. 计算过点 (2, 3) 和 (5, 7) 的直线的斜率？

Q2. 给定一条直线方程：y = 3x - 11，它的斜率是多少？

Q3. 如果一条直线的斜率为 5/6，且它经过点 (2, 5)，那么该直线的斜截式方程是什么？

Q4. 计算与直线 (0, -3) 和 (1, 11) 平行的直线的斜率？

Q5. 如果一条直线的斜率未定义，你能对该直线得出什么结论？

如果您喜欢此文章，请收藏、点赞、评论，谢谢，祝您快乐每一天。