C++ 检查四条线段是否形成一个矩形（Check if four segments form a rectangle）

给定四条线段，每条线段的端点坐标为一个坐标。我们需要判断这四条线段是否构成一个矩形。 
示例： 
 

输入：segments[] = [(4, 2), (7, 5),
                       （2, 4），（4, 2），
                       （2, 4），（5, 7），
                       （5, 7），（7, 5）]
输出：是

给定这些线段，制作一个长度为 3X2 的矩形。

输入：segment[] = [(7, 0), (10, 0),
                     （7，0），（7，3），
                     （7, 3），（10, 2），
                     （10，2），（10，0）]
输出：否

这些部分不能组成矩形。

如果您喜欢此文章，请收藏、点赞、评论，谢谢，祝您快乐每一天。 

上述示例如下图所示。

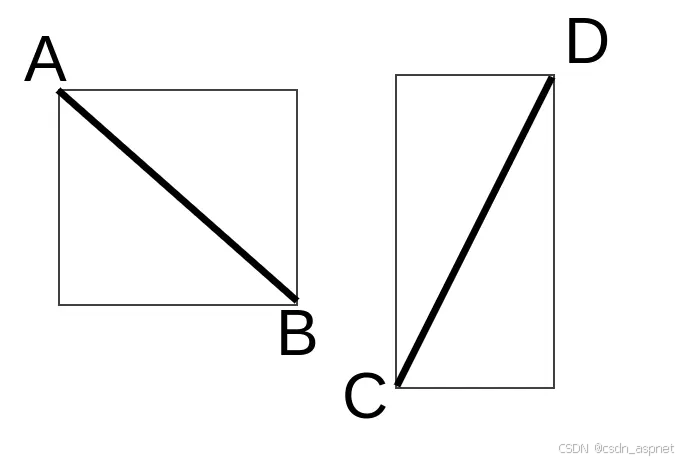
这个问题主要是如何检查给定的四个点是否形成正方形：

JavaScript 检查给定的四个点是否形成正方形：https://blog.youkuaiyun.com/hefeng_aspnet/article/details/149929118
C# 检查给定的四个点是否形成正方形：https://blog.youkuaiyun.com/hefeng_aspnet/article/details/149929017
Python 检查给定的四个点是否形成正方形：https://blog.youkuaiyun.com/hefeng_aspnet/article/details/149928893
Java 检查给定的四个点是否形成正方形：https://blog.youkuaiyun.com/hefeng_aspnet/article/details/149928798
C++ 检查给定的四个点是否形成正方形：https://blog.youkuaiyun.com/hefeng_aspnet/article/details/149928227

我们可以利用矩形的性质来解决这个问题。首先，我们检查线段的唯一端点总数，如果这些点的数量不等于4，则该线段不能构成矩形。然后，我们检查所有点对之间的距离，最多应有3个不同的距离，一个用于对角线，两个用于边。最后，我们将检查这三个距离之间的关系。对于构成矩形的线段，这些距离应满足勾股定理，因为矩形的边和对角线构成一个直角三角形。如果它们满足上述条件，则我们将由线段构成的多边形标记为矩形，否则不是。

示例代码：

// C++ program to check whether it is possible 
// to make a rectangle from 4 segments 
#include <bits/stdc++.h> 
using namespace std; 
#define N 4 

// structure to represent a segment 
struct Segment 
{ 
    int ax, ay; 
    int bx, by; 
}; 

// Utility method to return square of distance 
// between two points 
int getDis(pair<int, int> a, pair<int, int> b) 
{ 
    return (a.first - b.first)*(a.first - b.first) + 
        (a.second - b.second)*(a.second - b.second); 
} 

// method returns true if line Segments make 
// a rectangle 
bool isPossibleRectangle(Segment segments[]) 
{ 
    set< pair<int, int> > st; 

    // putting all end points in a set to 
    // count total unique points 
    for (int i = 0; i < N; i++) 
    { 
        st.insert(make_pair(segments[i].ax, segments[i].ay)); 
        st.insert(make_pair(segments[i].bx, segments[i].by)); 
    } 

    // If total unique points are not 4, then 
    // they can't make a rectangle 
    if (st.size() != 4) 
        return false; 

    // dist will store unique 'square of distances' 
    set<int> dist; 

    // calculating distance between all pair of 
    // end points of line segments 
    for (auto it1=st.begin(); it1!=st.end(); it1++) 
        for (auto it2=st.begin(); it2!=st.end(); it2++) 
            if (*it1 != *it2) 
                dist.insert(getDis(*it1, *it2)); 

    // if total unique distance are more than 3, 
    // then line segment can't make a rectangle 
    if (dist.size() > 3) 
        return false; 

    // copying distance into array. Note that set maintains 
    // sorted order. 
    int distance[3]; 
    int i = 0; 
    for (auto it = dist.begin(); it != dist.end(); it++) 
        distance[i++] = *it; 

    // If line seqments form a square 
    if (dist.size() == 2) 
    return (2*distance[0] == distance[1]); 

    // distance of sides should satisfy pythagorean 
    // theorem 
    return (distance[0] + distance[1] == distance[2]); 
} 

// Driver code to test above methods 
int main() 
{ 
    Segment segments[] = 
    { 
        {4, 2, 7, 5}, 
        {2, 4, 4, 2}, 
        {2, 4, 5, 7}, 
        {5, 7, 7, 5} 
    }; 

    (isPossibleRectangle(segments))?cout << "Yes\n":cout << "No\n"; 
}

输出： 

Yes

时间复杂度： O(n² logn) 

辅助空间： O(n)

如果您喜欢此文章，请收藏、点赞、评论，谢谢，祝您快乐每一天。