高等数学（总结1-导数的几个定理）

1）费马引理：

       证明的关键：如果在x0处可导，则在x0处的左导数等于右导数等于导数。
      意义：显然(x0，f(x0))是f(x)在x0邻域内的一个极值点，推广：f(x)的极值点（驻点），满足f'(x)=0.给出了求驻点的方法。
2）罗尔定理

     证明要点：连续区间存在最大值和最小值，费马引理；
     几何意义：连续区间[a,b],如果在开区间可导，且f(a)=f(b),则区间内至少存在一个驻点.
3）拉格朗日中值定理：
   

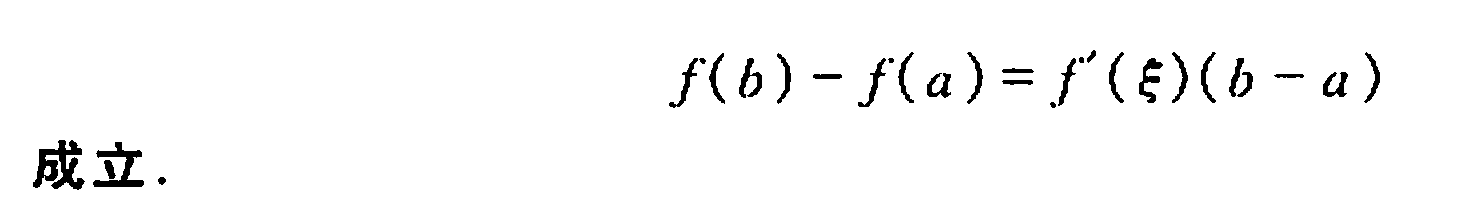
      证明要点：构造辅助函数G(x)=f(x)-f(a)-(x-a)(f(b)-f(a))/(b-a),罗尔定理.
      几何意义：在f(x)上一定存在一个点，过该点的切线平行于ab.
      其它意义：可以推出有限增量定理：f(x+Δx)-f(x)=f'(x+θΔx)Δx == Δy=f'(x+θΔx)Δx.

4）柯西中值定理

     证明要点：辅助函数 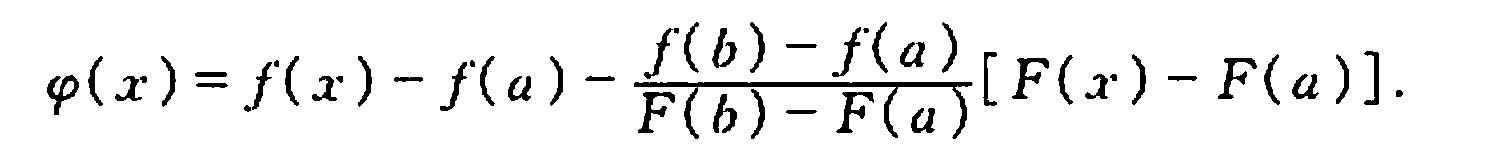和罗尔定理。