长期ROI预测技术方案综述

通过对游戏进行长期ROI预测，可以更准确地计算未来的收入和利润，帮助发行投放制定更准确的投放预算和策略，更好地分配资源，优化广告投放的投入，从而实现更高的投资回报。

曲线拟合法

在游戏行业中，曲线拟合算法是比较普遍的一种，以30日ROI预测360日ROI为例，根据历史的前360日的ROI数据得到一个拟合结果，再利用这个拟合结果，根据前30日ROI数据去拟合出未来360日ROI的预测值。常见的曲线拟合算法包括线性回归模型，逻辑回归模型，反正切函数模型，指数函数模型和幂函数模型。

线性回归模型

线性回归模型是一种用于预测因变量（响应变量）与一个或多个自变量（预测变量）之间关系的统计方法。最简单的形式是简单线性回归，其公式见下图，其中，y_是因变量，x是自变量，β0是截距，即当 x=0_x=0 时y的值，β1是自变量的回归系数，表示x每变化一个单位，y的变化量。

$$y={\beta }_0+{\beta }_{1}x$$

线性回归模型基于因变量和自变量之间的关系是线性的假设，通常使用最小二乘法估计参数，即通过最小化误差平方和来找到最佳拟合曲线。线性回归模型中的参数，截距和斜率，具有明确的统计意义，便于解释和理解。线性回归的典型曲线见下图：

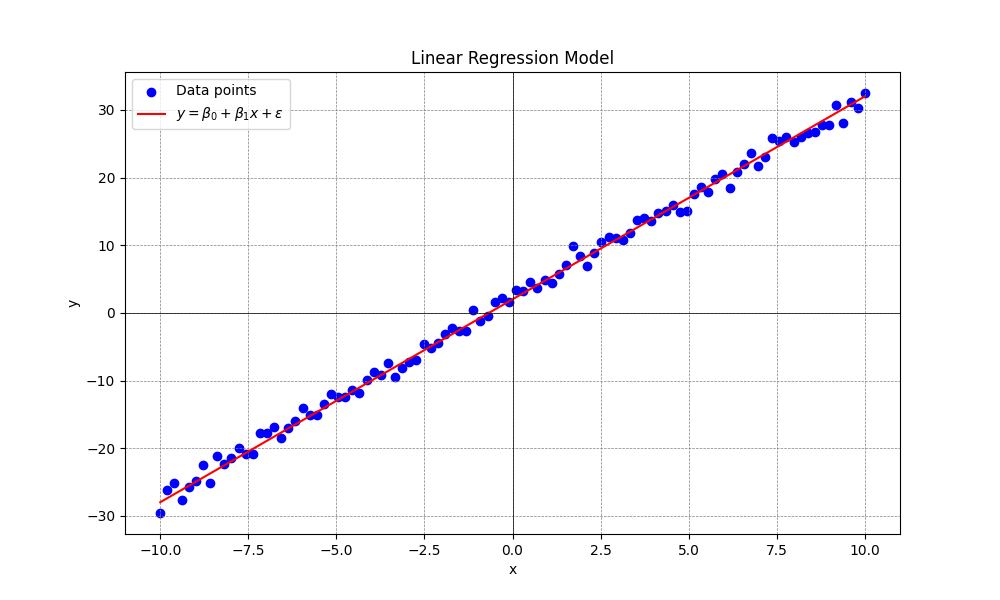
线性回归模型的优点是简单易用，计算方便，并且可解释性强，可以帮助理解变量之间的关系，适合处理各种不同情况的业务场景，能得到广泛应用。但线性回归模型的缺点也很明显，如果变量之间的关系是非线性的，模型效果会较差。同时，线性回归对异常值非常敏感，异常值可能会显著影响模型参数。总的来说，线性回归模型适合作为一个基线模型，提供了一个简单且易于理解的性能基准，帮助评估和比较更复杂模型的性能。

反正切函数模型

反正切函数模型是一种利用反正切函数进行拟合和预测的数学模型。反正切函数是一种常见的非线性函数，具有平滑的S形曲线特性，适用于描述一些非线性关系。其公式见下图，其中，y是输出预测值，x是输入特征，a是垂直缩放因子，b是水平缩放因子，c是幂次因子，arctan⁡是反正切函数。

$$y=a\cdot \arctan (b{x}^c)$$

反正切函数模型能够捕捉输入和输出之间的非线性关系，经过缩放和平移等变形处理后，可以拟合类似ROI衰减率的曲线，同时具有平滑的渐进特性，能够较好地描述渐进变化的过程，适用于一些复杂的实际问题。反正切函数的典型曲线见下图：