力扣DAY20 | 热100 | 旋转图像

前言

中等 √ 跟轮转数组的题解挺像。

题目

给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。

你必须在 原地 旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。

示例 1：

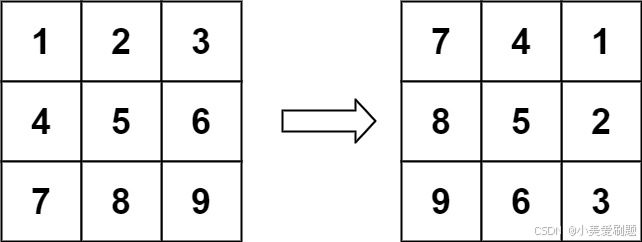
输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[[7,4,1],[8,5,2],[9,6,3]]

示例 2：

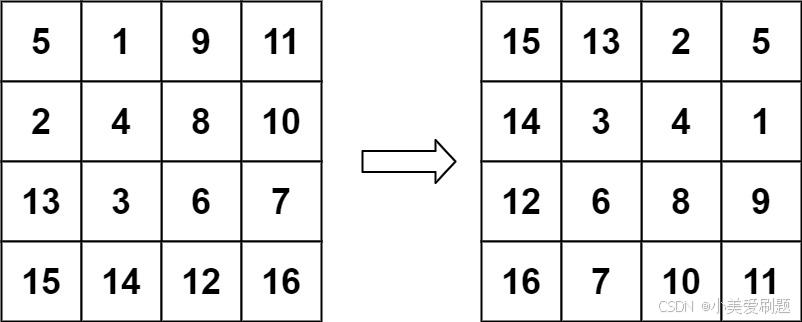
输入：matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
输出：[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]

提示：

• n == matrix.length == matrix[i].length
• 1 <= n <= 20
• -1000 <= matrix[i][j] <= 1000

思路

遍历一半的行，每行遍历对称位置。进入四个方位移动的循环。类似之前轮转数组的解法。

我的题解

class Solution {
public:
    void rotate(vector<vector<int>>& matrix) {
        int cur = matrix[0][0];
        int pre = cur;
        int m = matrix.size(), n = m;

        for (int i = 0; i < m/2; i++){
            for (int j = i; j < n-i-1; j++){
                int t = 4;
                cur = matrix[i][j];
                while (t--){
                    pre = matrix[j][n-i-1];
                    matrix[j][n-i-1] = cur;
                    cur = pre;
                    swap(i,j);
                    j = n - j - 1;
                }
            }
        }
    }
};

官方题解

原地旋转

题目中要求我们尝试在不使用额外内存空间的情况下进行矩阵的旋转，也就是说，我们需要「原地旋转」这个矩阵。那么我们如何在方法一的基础上完成原地旋转呢？

我们观察方法一中的关键等式：

matrix 
new
​    
 [col][n−row−1]=matrix[row][col]
它阻止了我们进行原地旋转，这是因为如果我们直接将 matrix[row][col] 放到原矩阵中的目标位置 matrix[col][n−row−1]：

matrix[col][n−row−1]=matrix[row][col]
原矩阵中的 matrix[col][n−row−1] 就被覆盖了！这并不是我们想要的结果。因此我们可以考虑用一个临时变量 temp 暂存 matrix[col][n−row−1] 的值，这样虽然 matrix[col][n−row−1] 被覆盖了，我们还是可以通过 temp 获取它原来的值：

{ 
​    
  
temp
matrix[col][n−row−1]
​    
  
​    
  
=matrix[col][n−row−1]
=matrix[row][col]
​    
 
那么 matrix[col][n−row−1] 经过旋转操作之后会到哪个位置呢？我们还是使用方法一中的关键等式，不过这次，我们需要将

{ 
​    
  
row
col
​    
  
​    
  
=col
=n−row−1
​    
 
带入关键等式，就可以得到：

matrix[n−row−1][n−col−1]=matrix[col][n−row−1]
同样地，直接赋值会覆盖掉 matrix[n−row−1][n−col−1] 原来的值，因此我们还是需要使用一个临时变量进行存储，不过这次，我们可以直接使用之前的临时变量 temp：

⎩
⎨
⎧
​    
  
​    
  
temp
matrix[n−row−1][n−col−1]
matrix[col][n−row−1]
​    
  
​    
  
=matrix[n−row−1][n−col−1]
=matrix[col][n−row−1]
=matrix[row][col]
​    
 
我们再重复一次之前的操作，matrix[n−row−1][n−col−1] 经过旋转操作之后会到哪个位置呢？

{ 
​    
  
row
col
​    
  
​    
  
=n−row−1
=n−col−1
​    
 
带入关键等式，就可以得到：

matrix[n−col−1][row]=matrix[n−row−1][n−col−1]
写进去：

⎩
⎨
⎧
​    
  
​    
  
temp
matrix[n−col−1][row]
matrix[n−row−1][n−col−1]
matrix[col][n−row−1]
​    
  
​    
  
=matrix[n−col−1][row]
=matrix[n−row−1][n−col−1]
=matrix[col][n−row−1]
=matrix[row][col]
​    
 
不要灰心，再来一次！matrix[n−col−1][row] 经过旋转操作之后回到哪个位置呢？

{ 
​    
  
row
col
​    
  
​    
  
=n−col−1
=row
​    
 
带入关键等式，就可以得到：

matrix[row][col]=matrix[n−col−1][row]
我们回到了最初的起点 matrix[row][col]，也就是说：

⎩
⎨
⎧
​    
  
matrix[row][col]
matrix[col][n−row−1]
matrix[n−row−1][n−col−1]
matrix[n−col−1][row]
​    
 
这四项处于一个循环中，并且每一项旋转后的位置就是下一项所在的位置！因此我们可以使用一个临时变量 temp 完成这四项的原地交换：

⎩
⎨
⎧
​    
  
​    
  
temp
matrix[row][col]
matrix[n−col−1][row]
matrix[n−row−1][n−col−1]
matrix[col][n−row−1]
​    
  
​    
  
=matrix[row][col]
=matrix[n−col−1][row]
=matrix[n−row−1][n−col−1]
=matrix[col][n−row−1]
=temp
​    
 
当我们知道了如何原地旋转矩阵之后，还有一个重要的问题在于：我们应该枚举哪些位置 (row,col) 进行上述的原地交换操作呢？由于每一次原地交换四个位置，因此：

当 n 为偶数时，我们需要枚举 n 2/4=(n/2)×(n/2) 个位置，可以将该图形分为四块，以 4×4 的矩阵为例：

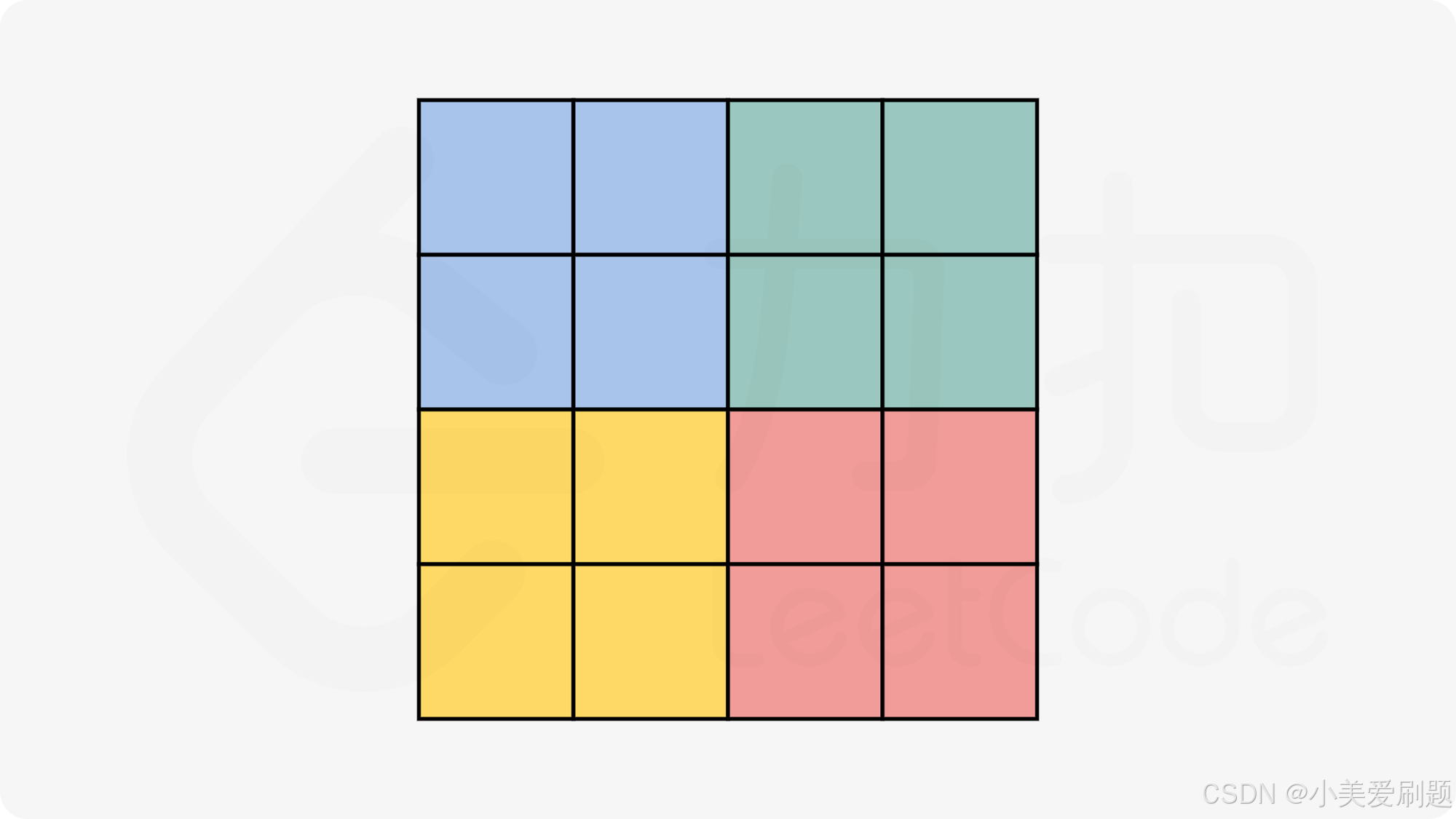
保证了不重复、不遗漏；

当 n 为奇数时，由于中心的位置经过旋转后位置不变，我们需要枚举 (n 2 −1)/4=((n−1)/2)×((n+1)/2) 个位置，需要换一种划分的方式，以 5×5 的矩阵为例：

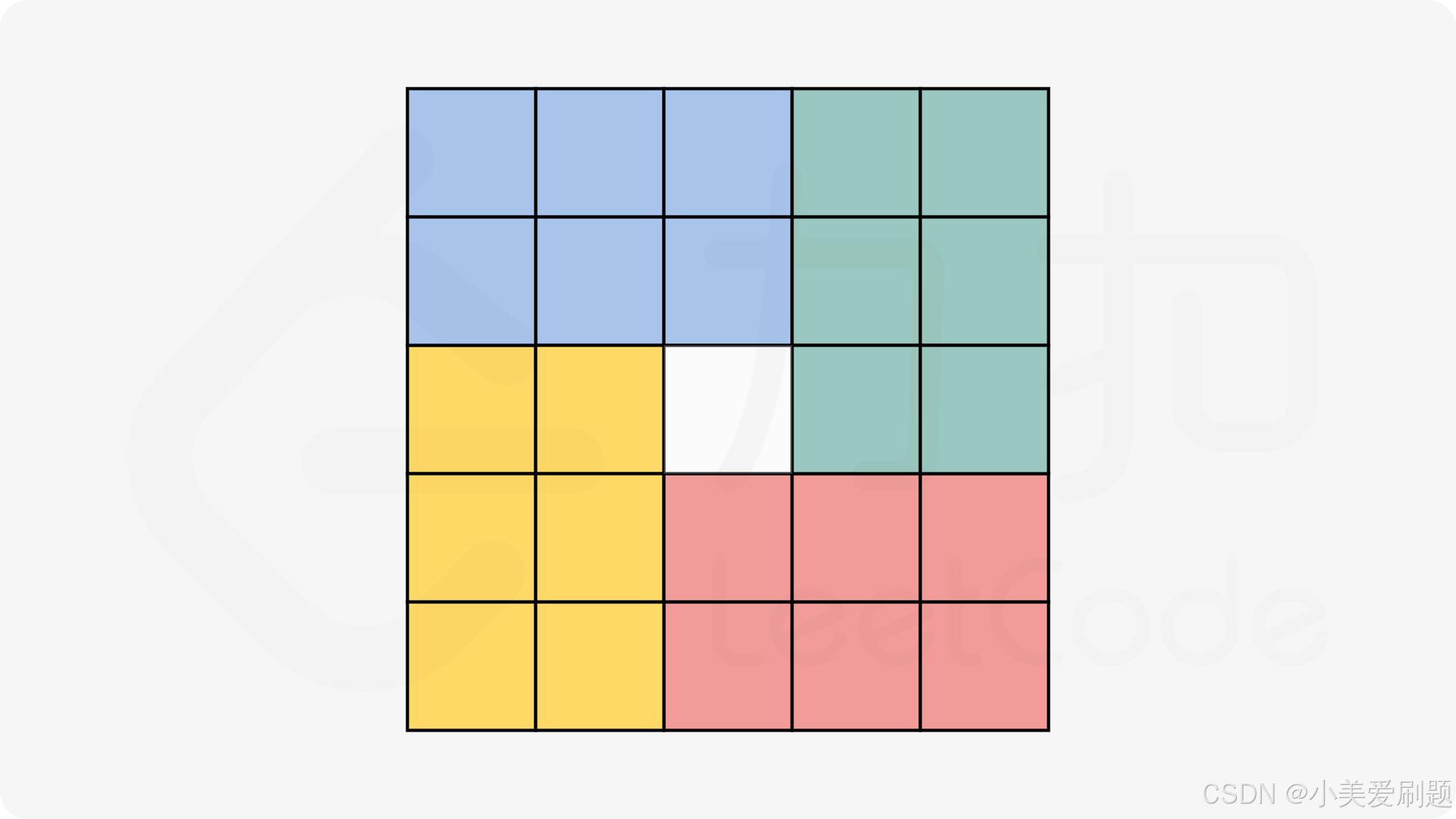
class Solution {
public:
    void rotate(vector<vector<int>>& matrix) {
        int n = matrix.size();
        for (int i = 0; i < n / 2; ++i) {
            for (int j = 0; j < (n + 1) / 2; ++j) {
                int temp = matrix[i][j];
                matrix[i][j] = matrix[n - j - 1][i];
                matrix[n - j - 1][i] = matrix[n - i - 1][n - j - 1];
                matrix[n - i - 1][n - j - 1] = matrix[j][n - i - 1];
                matrix[j][n - i - 1] = temp;
            }
        }
    }
};

用翻转代替旋转

我们还可以另辟蹊径，用翻转操作代替旋转操作。
对于水平轴翻转而言，我们只需要枚举矩阵上半部分的元素，和下半部分的元素进行交换，即

matrix[row][col] 
水平轴翻转
​    
 matrix[n−row−1][col]
对于主对角线翻转而言，我们只需要枚举对角线左侧的元素，和右侧的元素进行交换，即

matrix[row][col] 
主对角线翻转
​    
 matrix[col][row]
将它们联立即可得到：

matrix[row][col]
​    
  
水平轴翻转
​    
 matrix[n−row−1][col]
主对角线翻转
​    
 matrix[col][n−row−1]
​    
 
和方法一、方法二中的关键等式：

matrix 
new
​    
 [col][n−row−1]=matrix[row][col]
是一致的。

class Solution {
public:
    void rotate(vector<vector<int>>& matrix) {
        int n = matrix.size();
        // 水平翻转
        for (int i = 0; i < n / 2; ++i) {
            for (int j = 0; j < n; ++j) {
                swap(matrix[i][j], matrix[n - i - 1][j]);
            }
        }
        // 主对角线翻转
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < i; ++j) {
                swap(matrix[i][j], matrix[j][i]);
            }
        }
    }
};

心得

关键等式一致，明天再看此解法。