节能型汇聚节点布局研究

无线传感器网络中节能型汇聚节点布局

摘要

延长无线传感器网络的lif etime与其能耗密切相关，尤其是能量空洞问题， 即靠近汇聚节点的传感器节点因中继任务消耗大量能量。为缓解能量空洞 问题的影响，本文提出一种用于分析网络中可用能量的解析模型。下一步 是将总能耗建模为一个 k‐中值设施选址问题的解析模型，其解对应于网络 中 k汇聚节点的位置。
如解析法所示，当汇聚节点根据前述设施选址问题的解进行布置时， 总能耗最小化，从而实现更高的节能系统。因此，节省的能量可进一步利 用，例如延长网络寿命，并支持现代能量补充技术，如能量收集和电池充 电。
仿真结果验证了作为分析基础的分析模型，并确认了关于网络中可用
能量的结果。特别是，当…时观察到显著的节能效果
I部分工作最初发表于2012年4月1日至4日在法国巴黎举行的IEEE无线通信与网络会 议（WCNC2012）论文集中。
通讯作者电子邮件地址:gtsoum@ionio.gr(乔治ios·图马尼斯), okon@ionio.gr(康斯坦蒂诺斯·伊科诺莫乌),gkoufoud@ionio.gr(乔治ios·
库福达基斯),sonia.aissa@ieee.org(SoniaA¨ıssa)

1. 引言

无线传感器网络在过去几十年中经历了显著的发展，其成功反映了应 用领域的持续扩大[1],[2]。近年来的技术进步使得能够制造出小型且低成 本的传感器节点，这些节点可对目标区域进行监测并无线传输相应数据。
这种无线特性使得其可在传统布线成本高昂（例如大规模环境）、困难 （例如水下）甚至不可能实现（例如太空）的地方得到应用。
一方面，小型化和低成本使得在大规模环境中开发无线传感器网络成 为可能。另一方面，小型设备通常配备小型电池；由于是无线的，它们通 常在缺乏基础设施的情况下运行，因此依赖于有限电池提供的能量。尽管 能耗在无线网络中至关重要，但在其对应的传感器网络中，这一问题更为 突出[3]，主要原因在于能量空洞问题[4]。具体而言，传感器节点还充当 其他节点生成数据的中继，以将数据传输至负责收集所有感知信息的特定 节点——汇聚节点。因此，靠近汇聚节点的节点必须中继大量的流量负载， 因而其能耗相比那些流量负载较小的节点更高。这种无线传感器网络的特 性对传感器节点的能耗以及特别是网络寿命（即网络因节点电池耗尽而停 止运行的时间[5]）具有显著影响。
在延长网络寿命以减轻能量空洞问题影响方面已有大量文献，这些内 容在第2节中进行了全面回顾。本文采用的方法将汇聚节点位置问题（即 选择特定节点担任汇聚节点）表述为 k‐中位设施选址问题[6]（其中k为 网络中汇聚点的数量），并表明当根据以下方式选择汇聚节点时
中位数问题的解决方案可以最小化网络中的（平均）消耗的能量，从而利 用节省的能量延长网络的寿命。此外，如果将补充能量的技术与所提出的 解决方案结合使用，则可进一步增强可用（即节省）能量带来的益处。这 些技术包括能量收集[7],[8],[9]和充电[10],[11],[12],[13],，后者利用无线 能量传输技术[10],[11]并使用充电设备（例如，[13]）来实现其目的。
本文解决的第一个挑战是，在网络寿命和网络中的可用能量取决于多 种因素（例如，根据OSI术语，物理层的传输特性、数据链路层的媒体访 问控制和重传策略、网络层的路由方法等）的情况下，对其进行解析法建 模。此处的目的是推导出一个简单但有效的分析模型，以恰当地表示系统 的独特性。
对网络节点中可用能量的均值和方差进行了分析，并针对以树形拓扑 结构为案例研究的情况推导了相应的解析表达式，该案例研究的动机在于 数据通过路由树向汇聚节点转发。下一步是基于所提出的解析模型，将能 耗问题表述为一个设施选址问题。结果表明，当汇聚节点按照 k‐中位数解 进行部署时，网络整体消耗的能量最小化，从而实现绿色使用[14]。这是 本文解析部分的一个关键贡献，因为它将能耗问题与设施选址问题联系起 来，进而允许应用设施选址理论领域的工具和方法来解决所考虑的无线传 感器网络中的能耗问题。
虽然应对设施选址问题[6]的NP难性质超出了本工作的范围，但已存 在一些近似方法以及分布式方法，例如[15],，可用于特定的网络环境。
此外，通过仿真结果验证了所提出的分析建模方法及分析结果，假设 采用几何随机图[16],以适用于表示无线传感器网络拓扑。仿真结果的一个 贡献在于表明所采用的分析模型能够有效捕捉网络行为的某些重要方面。
关于分析结果，在仿真场景中观察到，当汇聚节点位于时，能耗达到最小
在分析推荐的那些节点上，相应的节能效果显著延长了网络寿命。

2. 过去的相关工作

Akyildizet al.在[1]和[2]中综述了无线传感器网络的基础。
Anastasiet al.[3]对能耗问题进行了回顾。Li和Mohapatra[4]以及 Liuet al.[17]研究了能量空洞问题及其对网络寿命的影响。在过去十年 中，大量研究致力于通过减轻能量空洞问题的影响来延长网络寿命，这些 研究主要关注传感器节点（例如中继节点的位置）或汇聚节点（例如多个 汇聚点、汇聚节点移动、汇聚节点定位），如下所述。

2.1. 传感器节点作为中继节点

特别是，Younis和Akkaya[18]综述了关于使用具有特殊能力的强
功能中继节点的各种方法（例如，增强的电池容量）。Lloyd和Xue[19]
通过采用近似算法研究了最小化中继节点数量的问题。Houet al.[20]通 过构建混合整数非线性规划问题来提出中继节点的部署方案，而
Halder和Bit[21]则提出部署异构中继节点以实现均匀的能耗。Chenet
al.[22]研究了具备特殊数据聚合能力的中继节点的部署。在[23]中，提出 了一种基于人工智能的中继节点部署策略。其他方法包括在混合移动社交 网络中的内容分发，例如[24]。

2.2. 汇聚节点位置

Efratet al.[25]考虑了两个关于基站（即本文术语中的汇聚节点）的最 优部署问题，以延长
网络寿命，并在给定视距约束的情况下覆盖特定区域。Bogdanovet al.[26]
将布置问题表述为最大流问题，而Oyman和Ersoy[27]则关注设计问题。
Liet al.[28]评估了用于通信成本降低的数据传输协调，Keskinet al.[29]提 出了一个集成传感器布置、调度、路径和移动汇聚点的轨迹的模型。
多个汇聚节点，如Vinczeet al.[30],所提出的，通过缩短到相应汇聚 节点的平均路径长度来降低能耗。Basagniet al.[31]更进一步引入了受 控汇聚点移动，从而在考虑此类移动实际限制的同时延长网络寿命。
Luo和Habaux[32]提出了一种沿网络边缘移动汇聚节点的策略，以平 衡能量消耗。Wanget al.[33]考虑了移动汇聚节点的实际限制，而Shi 和Hou[34]则对汇聚点移动与网络寿命提供了进一步的分析见解。
Papadimitriou和Georgiadis[35]提出了一种路由算法，能够应对由汇 聚点移动性带来的路由问题。Luoet al.[36]也提出了类似的思想。在其 开创性论文[37],中，Luo和Habaux将通过合适的汇聚点轨迹最大化网 络寿命的问题进行了建模，并证明了其NP难。在[38],中，设计了一种基 于机会路由理论选择中继节点的算法，以虚拟推导最优传输距离，实现节 能并最大化整个网络的寿命。

2.3. 将能耗问题作为设施选址问题

在无线传感器环境中，能耗问题具有一些其他网络（例如 vehic‐ular[39]）所没有的独特性。需要注意的是，本文考虑的方法确实 使用了基于全球定位系统（GPS）的方法，例如[40]。如前所述，本文从 设施选址视角来看待能耗问题，因此不同于之前提到的方法（ Mirchandani和Francis[6]对设施选址的一些初步成果进行了综述）。
设施选址方法本质上适用于解决部署问题，尽管它们会导致NP难问题，但
最近的近似方法适用于网络环境，例如Smaragdakiset al. [15]提出的
分布式近似方法。据作者所知，与本文最接近的研究是Krivitskiet al.
[41] 以及Oikonomou和A¨ıssa在相关工作中[42]的研究。在两者中
研究中，提出了一种关于汇聚节点位置的设施选址建模方法。特别是， Krivitskiet al.[41]引入了设施选址建模，重点关注最小化传感器环境中 的距离。该方法通过缩短距离间接降低了能耗，因为距离越短，为传输目 的所消耗的能量就越少。然而，在Krivitski的研究中，作者区分了两个重 要方面：（i）作者主要关注使用近似方法求解优化问题，而本文的重点则 主要集中于设施选址建模部分；（ii）对于他们所描述的设施选址建模部 分，并未考虑一些重要因素（例如流量负载），而这些因素正是本文建模 的基础。另一方面，Oikonomou和A¨ıssa[42],提出了1‐中位建模以减少 能量空洞效应；他们的主要关注点在于通过汇聚节点的移动来实现目标。
本文的工作将其建模扩展到多个固定汇聚节点（不允许移动）。

3. 提出的解析法系统模型

本节介绍了影响无线传感器网络运行的各种因素（如拓扑结构、能耗 等），并提出了一组假设，以便进行可行的分析。

3.1. 拓扑结构模型

网络拓扑由一个连通无向图 G表示，其中 V(G)为节点集合， E(G)为 它们之间的链路集合。集合 V的大小，记为 n，对应于网络中的节点数量
（即 n= |V(G)|）。如果两个节点 u和 v之间存在一条链路(u, v)（即(u, v) ∈ E(G)），则这些节点互为邻居，且它们之间可以直接进行传输。假设 每个节点 u占据一个由位置坐标确定的物理位置（不失一般性，为二维）。
若(u, v) ∈ E(G)，令 χ(u, v)表示节点 u和 v之间的相应欧几里得距离。若(
u, v)∈/ E(G)（即节点 u和v不是邻居），则这些节点之间存在一条最短路 径，我们令 x(u, v)表示在该最短路径上节点 u和 v之间各条链路的欧几里 得距离之和（称为最短路径欧几里得距离）。若(u, v) ∈ E(G)，则 x(u, v) = χ(u, v)。
汇聚节点收集无线传感器网络内的所有感知信息，并将其转发到网络 外部。因此，可以合理地假设每个汇聚节点都连接到某种类型的基础设施
（例如，具有充足连接性和丰富电源的节点）。假设 k sinks位于网络中 的 k个不同位置。令s表示一种特定的汇聚节点部署，即作为汇聚节点的 特定节点集合（显然， |s| = k）。每个节点 u ∈ V（G）仅由一个汇聚节 点服务（即， u在整个网络运行过程中将其数据包传输到同一个汇聚节点），
记为 s（u），该汇聚节点是距离节点 u欧几里得距离最短的那一个，即 x
（u, s（u））= mins∈s x（u, s）。

3.2. 能量消耗模型

假设节点 u即将向其邻居节点 v传输（即(u, v) ∈ E(G)），令 w(u,
v)表示此次传输所消耗的能量。此处考虑对称链路，因此从节点 u到节点
v的传输能耗与反向传输相同。一个常用的能耗模型([43])表示为：w(u, v)
= µχγ(u, v)+ν，其中：(i) ν是设备操作（如感知）所需的恒定能量消耗， 与距离无关；(ii) µ是一个常数因子；(iii) γ是路径损耗因子，主要由周 围环境决定（在开放空间中为 γ= 2，而在密集环境（如建筑物）中，其 值可高达五[43]）。鉴于无线传输中的主导因素是实际传输所消耗的能量， 因此 ν与 µχγ(u, v)[44],相比可忽略不计。
w(u, v)= µχγ(u, v). (1)
消耗的能量 w(u, v)将被视为节点 u 和 v 之间链路的权重，并称为 链路(u, v)的链路权重。假设两个节点 u 和 v之间存在一条最短路径，
沿该路径所有链路权重的总和称为能量距离，记为 d(u, v)。显然， d(x, y)
对应于数据包经由特定最短路径传输时所消耗的总能量。也就是说， d(x, y)等于生成该数据包的节点所消耗的能量与将该数据包转发至汇聚节点的 各个节点所消耗的能量之和。需要注意的是，当考虑最短路径欧几里得距 离x(u, s)时，两个节点 u 和 v之间的最短路径，在链路权重 w(u, v)被 考虑的情况下（假设所有网络链路的 µ 和 γ 相同）也仍然是最短路径。
这是因为 w(u, v)和 x(u, s)均依赖于欧几里得距离。
χ(u, v)（注意，如果 f> g+ h，则 fe> ge+ he，对于任意正数 f, g, h和e ≥ 1）。

3.3. 媒体访问控制和重传模型

所采用的媒体访问控制（MAC）策略以及其他因素（如重传）也会影 响消耗的能量[45]。例如，如果采用允许发生碰撞的MAC策略（如基于竞 争的策略），则重传不可避免。即使采用无冲突的基于时分多址的媒体访 问控制（TDMA‐basedMAC），由于无线介质导致的错误传输（如信道 条件差、邻近节点干扰）仍可能发生，从而需要对同一数据包进行重传。
由于本研究的重点并非媒体访问控制，在解析法部分我们假设所采用的 MAC协议能够成功传输数据包且不发生碰撞。在仿真部分，则将基于更现 实的场景，采用载波侦听多路访问/冲突避免（CSMA/CA），因此会发生 碰撞以及重传。需要注意的是，所采用的MAC策略和重传策略均会影响时 延和丢包，这两个参数对网络的整体行为至关重要。例如，由于时间限制， 延迟的数据包可能变得过时，从而导致能量的不必要消耗。同样，丢包也 需要重传，造成额外能耗。本文采用的方法是通过选择汇聚节点的位置来 降低总能耗，因此对MAC策略和重传策略的进一步研究不在本文范围之内。

3.4. 路由模型

路由支持数据包在邻居节点之间中继传输至汇聚节点。尽管多年来已 提出了许多复杂的能量感知路由协议，例如[46],[47],[48],[49],本文采用 了一种简单的最短路径路由方法[50], ，假设链路权重为 w（u, v），如公 式(1)所示。这里采用了这种本质上具有能量感知且简单的路由策略，尽管 该分析可适用于任何生成路由树的路由策略。
假设节点 u，则以相应汇聚点 s(u)为根节点创建一棵最短路径树。
给定网络中有 k ≥ 1 个汇聚节点，则存在 k 棵不同的最短路径树，每棵 树的根节点为一个（不同的）汇聚节点。对于汇聚节点部署 s，设 Ts(u) 表示由前述最短路径所构建的最短路径树中以根节点 u为根的子树
路由策略。在此表示法下，以汇聚节点 s(u)为根节点的最短路径树（也称 为路由树）记为 Ts(s(u))。 （圆圈内） 时的最短路径（路由）树链路。虚线表示其余的网络链路，即 E(G)\ E(Ts(s(u)))。虚线 区域内的部分属于子树 Ts(u)。粗箭头表示总流量负载，虚线箭头表示移动到节点 v 后 返回汇聚节点的充电装置。本示例中，s(u)=s(v)。)

3.5. 流量负载模型

当在某个节点 u生成的数据包到达某个节点 v时，节点 v应将其进一 步转发至汇聚节点 s(u)，此外还需转发节点 v自身生成的任何数据包。假 设节点的内部存储器足以满足任何排队需求。
设 λu表示在任意时间单位内某个节点 u生成数据包的概率，称为该 节点 u的流量负载。给定一种汇聚节点部署方案 s，令Λs(u)表示节点 u的 总流量负载，其值由下式给出
Λs(u)= ∑
v∈T s(u)
λv. (2)
图1描述了一个示例网络，并以图形方式说明了最短路径树，假设根汇聚 节点为 s(u)，其中某些节点为 Ts(u)和Λs(u)。图中所示的粗箭头对应于 数据包通过网络链路向汇聚节点转发的路径。

3.6. 电池模型

设 Bs u(t)表示在给定汇聚节点部署 s的情况下，节点 u的电池在时间 t
时的剩余能量。令 Bmax表示节点电池的容量。假设在网络生命周期开始
时（即 t= 0），所有节点均充满电，则 Bs u(0)= Bmax， ∀u ∈ V(G)。
鉴于传输是主要的能耗因素，如果从节点 u向节点 v进行传输，则节 点 u电池的能量水平预计将减少 w(u, v)。假设没有传输错误，并且所采用 的MAC策略能够避免碰撞，那么在时间段[0, t]内，节点 u预计（平均）将 传输 Λs(u)t个数据包，从而（平均）消耗Λs(u)w(u, v)t能量单位。因此， 在时间 t时节点电池的平均能量水平为
Bs u(t)= Bmax −Λ s (u)w(u, v)t, (3)
其中(u, v) ∈ E(G)。在分析中，假设所有网络链路的链路权重相等，因此它们
被归一化为1，即 w(u, v)= 1, ∀(u, v) ∈ E(G)，或 Bs u( t)= Bmax −Λ s (u)t。

4. 可用能量分析

在终止时间 T(s)时网络中的可用能量，对于进一步理解无线传感器 网络中能耗的影响至关重要。根据公式(3)和公式(4)，并假设链路权重相 等，则在网络中任意节点 u 在时间 T(s)剩余的能量为
Bs u(T(s))= Bmax(1 − Λs(u) Λs(s)) . (5)

4.1. 平均可用能量

此处关注的是网络在时间t, E[B s u( t)],的平均可用能量作为平均总流量
负载 E[Λ s(u)],的函数，其中E[·]= 1 n∑u ∈ V(G)( ·)。根据公式(3)，
E[B s u(t)]= Bmax −E[Λ s (u)]t. (6)
由公式(4)可证明以下引理。
引理1.在时间 t= T(s)的平均可用能量由下式给出
E[Bs u(T(s))]= Bmax(1 − E[Λs(u)] Λs(s)). (7)
为了进一步理解 E[Λ s
( u]
Λs s )()的本质（以及相应的 E[Bs u(T(s))]），将l-ary树形拓扑作为案例研究。为简化起见，在 l‐ary树的案例研究中仅考虑单 一汇聚节点（k= 1）的情况，尽管以下结果可轻松推广至 k ≥ 1的一般情况。
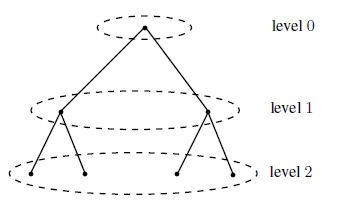
一种 l‐ary树（如图2所示）由层数 m和每个节点的子代数量 l所表征，其中
根节点为汇聚节点。节点数量由 n=∑ m−1 i=0 li给出。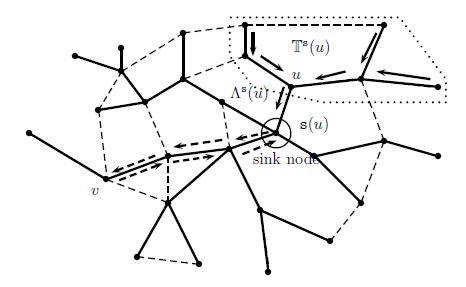
图2所示的例子对应一个 l‐ ary树，其每层分支数l为 l= 2，层数m为 m= 3，节点数量为 n= 7。
将 l‐ary树作为特殊拓扑情况引入的动机在于路由树的存在，该路由树 决定了数据包到达相应汇聚节点的路径。尽管对于某些拓扑结构而言， l‐ ary树可能并非路由树的精确近似，但解析结果能够捕捉网络的行为特性， 这一点将在后续通过仿真结果加以证明。
引理2。假设所有网络节点的流量负载为常数 λ，且考虑一个具有 m层的 l-叉树
情况，则该 l-叉树中第i层（i= 1,…, m− 1）节点的总流量负载，记为 Λ i，由
l m− i − 1 l − 1 λ给出。
图3展示了 Λi作为5层三叉树中层数 i的函数的变化情况。同时描绘 了第 i层（即 li）对应的节点数量。这里一个有趣的观察是，较大的 Λi值 （即较小的 i值）对应较少的节点数量，而随着 Λi的减小，相应的节点数 量呈指数级增长。这实际上是能量空洞问题的图示说明，因为靠近汇聚节 点的少数节点相比远离汇聚节点的节点承受更高的总流量负载。
定理1。假设存在一个汇聚节点，所有网络节点的流量负载恒定 λ以及 l-叉树
具有 m层的情况，则可以证明E[Λ s ( u]
Λ s s
)()=(n(l−1)+1) logl(
n −n n 2 l−1
.
(l−1)+1)
()
推论1。对于一个汇聚节点和具有 m层的2-叉树， E[Λ s
( u]
Λ s s
)()
=
(n+1) lo g
2 −n n 2 → lo g 2 n+1 ()(n)n；对于完全图， E[Λ s
( u]
Λ s s
)()
= 2n−1 n 2 → 2 n。
定理1和推论1进一步阐明了 E[Λs ( u]
Λs s
)()的行为，该行为是网络中剩余 能量的重要组成部分，如公式(7)所总结的。图4给出了一个示例。特别是，
左侧y轴描绘了定理1给出的 E[Λs ( u]
Λs s
)()，其作为 l(l ≥ 2，因为 l= 1的情 况对应于单线拓扑结构)和 n= 1000的函数。对于较小的 l值，所得结果接 近推论1给出的 log2(n) n。随着l的增加，（密集）曲线收敛到某个点，即推
论1给出的极限2 n。实际上，随着 l的增加，网络中邻居节点的数量也增加， 其上限为完全图。
()和 V ar Λ s (u) 2作为 l ≥ 2的函数（假设为 l‐ary树）以及 n= 1000。)

4.2. 可用能量的方差

引理1建立了 E[Λs(u)]与 Λs(s)之间的关系。特别地， E[Λs(u)]越接近 Λs(s)，网络中剩余的能量就越少。需要注意的是，能量空洞问题的一个 表现是某些节点的电池已耗尽，而其他节点几乎未被使用，从而表明存在
能量不平衡水平[21]。这种“不平衡”的度量是可用能量的方差， V ar[B s u
(T(s))]= E[(B s u( t))2]−E 2 [B s u( t)],，如下所述。
引理3。在时间 t=T（s）时，网络中可用能量的方差由以下公式给出
V ar[Bs u(T(s))]= B2 max
V ar[Λs(u)]
(Λs(s))2
. (8)
以下定理重点关注 l‐元树的情况。
定理2。假设存在一个汇聚节点，所有网络节点的流量负载恒定 λ ，以
及一个具有 l个分支的树形结构，共 m层，则可以证明V ar Λs(u) 2=
(n(l− 1)+ 1)n2l−(n(l−1)+1)log2l(n(l−1)+1)n4(l−1)2 .
定理2给出了关于 V ar Λs (u) 2的解析表达式，有助于进一步理解 在给定 l和 n值时网络中的可用能量。接下来给出二叉树（即二元树）和 完全图（即所有节点均相互连接）对应的边界。
推论2。对于一个汇聚节点和一个具有 m层的二叉树， V ar Λ s
(u) 2=(
n+1)2n 2 −(n+1)log 2 2 n+1
n4 → 2 n
()，而对于完全图， V ar[Λ s
(u) ] 2=(n−1) 3 n4 → 1 n(Λ s (s))。
定理2和推论2进一步阐明了 V ar Λ s
(u) 2在特定 l和 n取值下的行为。
这一点也在图4中以图形方式进行了说明。特别地，图4的右侧y轴还描绘了
根据定理2给出的 V ar Λ s
(u) 2 ,，作为 l和 n= 1000的函数。当 l取
较小值时，所得结果接近推论2给出的2 n 。随着 l增大，该（虚线）曲线收
敛至某一特定点，即推论2给出的极限 1 n 。

4.3. 能耗与汇聚节点放置

汇聚节点部署的变化可能会导致网络中的能量消耗不同，如下述引理 所述。设 s1表示某一汇聚节点部署， s2表示另一汇聚节点部署。根据
公式(6)，则有E[B s 1 u(t)]= Bmax − E[Λ s 1(u)]t和 E[B s 2 u(t)]= Bmax − E[Λ s 2(u)
]t。下述引理被提出并证明。
引理4。对于任意两个不同的汇聚节点位置，记为 s1 和 s2，在时间 0< t ≤ T(s)成立，
E[Λs1(u)]< E[Λs2(u)] ⇔ E[Bs1 u(t)]> E[Bs2 u(t)].
显然，通过改变汇聚节点的位置可以最小化消耗的能量。这促使了下一节 中提出的汇聚节点布局分析。

5. 能量消耗最小化

根据引理4给出的动机，进一步研究了汇聚节点的最优位置，即在任 何时刻 t最大化网络中平均可用能量的特定汇聚节点部署。因此，需要求 解方程
E[B(sE) u(t)]= max
s E[Bs u(t)], (9)
其中 sE表示最优能量汇聚节点布局。
为了进行分析，假设在任意节点 u生成一个数据包。该数据包将通过 以 s(u)为根节点的路由树向汇聚节点 s(u)转发。因此，消耗的能量由能量 距离 d(u, s(u))给出。平均而言，每个时间单位在节点 u生成 λu个数据包； 因此，在节点 u生成的数据包所消耗的平均能量等于 λud(u, s(u))。对于 汇聚节点部署 s以及所有网络节点，平均网络消耗能量记为 E(s)，其表达 式为
E(s)= ∑
u∈V(G)
λud(u, s(u)). (10)
以下定理揭示了在时间 t时网络中的平均可用能量与消耗的能量之间的一 个非常有用的关系。
定理3。对于网络中的任意两个汇聚节点位置，记为 s1和 s2，有
E[Λ s 1(u)]< E[Λ s 2(u)] ⇔ E(s1)< E(s2).
根据定理3和引理4，推论3得证。
推论3.对于网络中的任意两个汇聚节点位置，记为 s1 和 s2，均有
E[Bs1 u(t)]> E[Bs2 u(t)] ⇔ E(s1)< E(s2).
鉴于推论3对 t= T(s)同样成立，则可得出结论：满足 E[B(sE u)(T(s))]=
maxs E[B(s) u(T(s))],的最优能量汇聚节点布局 sE 同时也满足 E(sE)=mins E(s)。
最终，网络中可用能量最大化的问题（即公式(9)）被转化为基于网络 平均消耗能量的最小化问题，如公式(10)所示。进一步分析公式(10)可知， 上述优化问题实际上是一个设施选址问题，特别是 k‐中位数问题[6],，后 一发现是本文的核心贡献。
根据文献（例如，[6]）可知， k‐中位数问题是一个需要全局信息的大 型优化问题（例如，NP完全），因此在无线传感器环境中不切实际。可根 据具体情况采用各种近似技术来降低问题的复杂性。例如，可采用易于实 现的分布式“爬山法”技术（如[15],[51],），以减少对更高计算能力和全 局信息的需求，同时适应网络的动态变化。需要注意的是，这些近似方法 和分布式方法是在设施选址领域内进行分析研究的，不在本工作的讨论范 围之内。

6. 仿真结果与评估

采用OMNeT++模拟器[52]来构建仿真场景。汇聚节点被视为基础 设施的一部分，其电池持续充电，并作为相应最短路径路由树的根节点。
仿真场景中网络参数及其对应值如表1所示。具体而言，每个节点 u根据 其流量负载 λu生成数据包，每个数据包通过所述路由树向相应的汇聚节 点转发。流量负载 λu取均匀分布在范围[0, 1/n]内的随机值，其中 n为节
点数量，因此平均值为 E[λu]= 1 2n 。当发生数据包传输时，能量消耗按照
公式(1)进行计算，假设每个节点消耗的能量相同，且不失一般性， γ= 3
和 µ= 1为公式(1)中选定的取值。
仿真场景，除非另有说明。具体而言，如果要从节点 u 向节点 v进行数 据包传输，(u, v) ∈ E(G)，则节点 u的电池电量将减少 w(u, v)= r3c。
每个节点的初始可用能量设置为 Bmax= 1。

6.1. 仿真元素

所开发的仿真场景依赖于OMNeT++仿真器[52]库中可用的某些软件 包。如前所述，为了逼近实际情况，仿真中采用了CSMA/CAMAC策略。
CSMA/CAMAC属于OMNeT++仿真器库的一部分，更具体地说，属于 INET框架[53]。根据CSMA/CA，在仿真过程中可能发生碰撞，导致数据 包重传。此外，OMNeT++仿真器中的CSMA/CA确认(ACK)功能已启用， 即节点 u在成功接收来自节点 v的数据包后，会发送一个ACK（确认） 消息。传输ACK所消耗的能量设置为传输一个（较大）数据包所消耗能量 的五分之一。若在传输后未收到ACK，则进行重传。下文为简化仿真结果 的呈现，首先考虑单个汇聚节点（k= 1）的情况，而多个汇聚点（k> 1） 的结果则在最后的单独小节中给出。

参数	值
网络区域	[0, 1] ×[0, 1]
节点数量 n	1000
连通半径 rc	0.06
流量负载 λu	[0, 1/n]
节点初始能量 Bmax	1
数据包传输能量 w(u, v)	r3 c
ACK传输能量	r 3 c 5

6.2. 几何随机图拓扑

在仿真中，考虑了[0, 1]×[0, 1]网络区域中 n= 1000个节点的连通几何随 机图拓扑[16]，因其最
适合捕捉传感器网络拓扑结构的特殊性[54]。在这种拓扑结构中，如果两 个节点之间的欧几里得距离小于或等于连通半径 rc，则它们之间存在连接。
给定公式(3)，可以推导出关于可用能量 Bs u(t)的解析表达式，前提是 几何随机图中任意邻居节点之间的欧几里得距离以 rc为上界。此外，实 际数据包传输所消耗的能量中额外有五分之一用于后续的确认信息。由于
在负载 E[λu]= 1 2n较低的情况下碰撞数量较少，重传的数据包所消耗的总
能量被认为很小。因此，对于几何随机图和 Bmax= 1， Bs u(t)=1 −Λs(u)
r3ct− 1 5Λ s(u)r3ct成立。
Bs u(t)=∼ 16/5Λs(u)r3ct. (11)
这个表达式用于推导出进一步的结果，如下一个引理所示。
引理5。对于一个 n= 1000和 rc=0.06的连通的几何随机图，存在关于终
止时间 T(s)以及网络节点剩余的平均可用能量 Bs u(T(s))的表达式，使得
T(s) ≥ 5
3r3 c ，且 E[Bs u(T(s))]= 1 − 6/5(n+1) log 2 −n
2n2 r3cT(n+1)(s)。
尽管 rc的取值可高达√2，但可以确定的是，在这些情况下，相应的拓 扑结构具有小直径和大量邻居节点，与典型的无线传感器网络不相似，因 为在典型的无线传感器网络中，传感器节点通常广泛分布且具有低传输范 围。表2展示了针对不同 rc值的几何随机图在网络直径和邻居节点平均数量
2|E(G)|
n 方面的仿真结果快照。可以看出，当 rc> 0.75时，网络直径过小 （接近2），每个节点平均将79.4%的网络节点作为其邻居。我们的研究重 点将放在 rc ≤ 0.4的取值上，因为它们对应于具有大直径和少量邻居节点的 网络拓扑。

rc	0.06	0.1	0.2	0.4	0.75	1.0	√2
直径	30	16	8	4	2	2	1
2|E(G)| n	10.8	28.3	102.6	340.9	794.2	972.2	999

6.3. 流量负载

图5‐a描绘了关于 E[Λ s
( u]
Λ s s
)()和 V ar Λ s
(u) 2 ,的仿真结果（带
点的线条）和解析结果（孤立的点），作为 r c的函数
以及 n= 1000。左侧y轴对应于 E[Λs ( u]
Λs s
)()，右侧y轴对应于 V ar Λs (u) 2。该网络拓扑的解析结果是通过绘制定理1中的解析表达式得到的，而 l
的具体数值则是从仿真结果中提取的。
在两种情况下，均观察到随着 rc的增加，解析法和仿真结果均收敛。
随着 rc的增加，拓扑结构开始趋近于完全图。对于 E[Λs
( u]
Λs s
)()的情况，
其收敛值为2 n，即推论1给出的期望边界；而对于V ar Λs(u) 2,的情况，
其收敛值为 1 n，如推论2所述。当 rc取值较小时，网络拓扑结构远离完全图，
尽管它并非树结构[16],，但值得注意的是，推论1（即 log2(n) n ≈ 0.0099）
和推论2（即 2 n= 0.002）所给出的边界与仿真中观察到的值接近。这表明 对应于 rc= 0.06的拓扑结构可用二叉树近似。
E[Λ s ( u] Λs s )()和 V ar Λ s (u) 2 , 随 rc变化的函数关系；(b)在时间 t= 5000时， Bs u(t)随两个任意选定的汇聚节点位置s1 和s2对应的 Λs(u)变化的函数关系；(c)在时间 t= 5000时， Bs u(t)随 Λs(u)变化的函数关系，对应 rc 的三个取值（0.20、0.30和0.40）；(d) E[B s u(5000)]随 E[Λ s(u)]变化的函数关系；(e) E[B s u(5000)]随能量比 E(s) E (sE)变化的函 数关系；(f) V ar[B s u(10 4)]随能量比 E(s) E (sE)变化的函数关系；(g) T(s)随能量比 E(s) (sE)变化的函数关系；(h)在终止时间 T(s)时， E[B s u(T (s )) ]随能量比 E(s) E (sE)变化的函数关系；(i)在终止时间 T(s)时， V ar[B s u(T (s )) ]随能量比 E(s) E (sE)变化的函数关系。)

6.4. 可用能量

图5‐b描述了在时间 t= 5000对于rc= 0.06，两种不同且任意选定的
汇聚节点位置 s1 和s2下与 Bs u(t)相关的仿真结果。图5‐b的 y‐轴对应
于 Bs u(5000)， x‐轴对应于每个节点 u的总流量负载 Λs(u)。每个描绘的
点对应于特定汇聚节点位置下某个单独节点的Bs u(5000)（因此共描绘了 2000个仿真点，即汇聚节点位置 s1对应1000个点，汇聚节点位置 s2对 应1000个点）。一个初步观察结果是，大多数点集中在图的左上角。这与 引理2一致，实际上也是能量空洞问题的另一种图形化表现，其中某些节 点消耗的能量比例显著高于其他节点。
公式(11)的解析表达式也在图5‐b中以虚线表示。后者对应于函数 1−6/5Λ s
(u)r 3 c t= 1−1.296Λ s (u)。
并且如观察所示，对于两个汇聚节点，在给定Λs(u)值的情况下，它能有效
逼近 Bs u(5000)。需要注意的是，该分析是在某些假设条件下进行的（例如， 未考虑重传问题），而仿真程序更接近实际情况（例如，数据包被排队、 丢失、重传等）。然而，该分析仍能够捕捉到系统的行为，如图5‐b所示。
这也体现在
图5‐c展示了不同连通半径 rc以及一个任意选定的汇聚节点的情况。

6.5. 汇聚节点部署

到目前为止，汇聚节点的位置是在网络节点中任意选择的。在下文中， 所展示的仿真针对汇聚节点所有可能的 n个位置（排列）进行。特别是， 图5‐d描绘了在时间 t= 5000时每个网络节点的平均剩余可用能量，表示为
E[Bs u(5000)],，其作为平均总流量负载 E[Λsu]的函数。每个点对应一个不 同的汇聚节点位置（总共n= 1000个）。可以观察到，随着平均总流量负 载的增加，平均可用能量减少，这与引理4一致。
令 E(s) (sE)表示能量比，该函数说明了特定汇聚节点部署下（平均）网 络消耗能量与最优值（即E(s) E(sE) → 1）的接近程度（显然，对于任意汇聚
节点部署， E(s) (sE)≥ 1）。图5‐e以能量比为函数，描绘了与图5‐d相同的
结果。显然，随着 E(s) (sE)的增加，平均可用能量 E[Bs u(5000)]减小，这明 确表明当汇聚节点部署接近最优时（即由公式(10)给出的 k‐中位数问题的
解），网络在某一时刻t< T(s)的剩余能量更高。相应的方差 V ar[Bs u(10 4)
],也在图5‐f中显示，随着能量比的增加而增大，因此当能量比最接近最优 时，网络节点中的剩余能量更加均匀。

6.6. 网络寿命

图5‐g描述了关于终止时间 T(s)作为能量比 E(s) (sE)的函数的仿真结 果。与能量比接近2时的 5× 103相比，某些节点（即当 E(s)
E (sE)→ 1时，接 近 5 × 104）的终止时间大约增加了10倍。显然，正是那些能量比接近1的 节点使得终止时间得以增加。这表明未消耗的能量被利用来延长网络的寿 命。
图5‐h和图5‐i描绘了可用能量的均值（方差）随能量比的变化函数，类似于图 5‐e和图5‐f。显然，图5‐h（图5‐i）中没有出现与图5‐e（图5‐f）类似的模式。
这归因于这样一个事实：在先前的场景中未使用的可用能量在此场景中已 被利用，以延长网络的寿命。
网络在 t=T(s)时的平均可用能量 E[Bs u(T(s))]随终止时间 T(s)的变
化如图6‐a所示。引理5给出的 Bs u(T(s))的解析解也在图6‐a中描绘出来， 并且捕捉到了仿真结果所显示的系统行为。
)]作为终止时间 T(s)的函数；（b） T(s)作为 rc的函数。对于每个点， 还标出了 T(s)观测到的最大值和最小值。虚线对应于引理5给出的解析解。)
图6‐b描述了终止时间 T(s)作为 rc的函数。每个点对应于在所有 n
可能的汇聚节点位置上的平均终止时间。对于每个点，所示上界对应于该 特定场景下 T(s)的最大值，下界则对应于最小值。同时给出了由引理5给
出的解析法边界 T(s)= 5 3r 3 c
。随着 rc 增大，终止时间减小。

6.7. 多个汇聚节点

本小节介绍了 k> 1的情况（k= 2,3,4）。为了便于阅读，针对 k> 1
所呈现的结果对应于先前已研究过的 k= 1的仿真场景。此外，由于 k中位 数问题的NP难性质，为减少所需的计算能力，考虑了一个任意选取的
n= 1000排列子集，而非全部( n k) 种可能的排列。
图7‐a描述了在与前述相似的场景中，汇聚节点Bs u( t)在时间t= 5000时的剩
余能量随 Λ s (u)变化的函数关系
如图5‐b所示，同时绘制了解析表达式。显然，对于 k> 1，该分析仍能 捕捉到网络的行为。同样的观察结果也适用于图7‐b，该图展示了类似图
6‐a场景下 E[Bs u(T(s))]作为终止时间 T(s)的函数。如图所示，解析表达 式成功地捕捉到了网络的行为。
时间 t= 5000时 Bs u(t)作为 Λs(u)的函数。(b) E[Bs u(T (s))]作为终止时间 T(s)的函数；(c) E[Λ s ( u] Λs s ()()作为 rc的函数；(d) T(s)在 k= 2条件下作为近似能量比 E(s) E (ˆsE)的函数；(e) T(s)在 k= 3条件下作为近似能量比 E(s) E (ˆsE)的 函数；(f) T(s)在 k= 4条件下作为近似能量比 E(s) E (ˆsE)的函数。)
图7‐c描述了 E[Λ s
( u]
Λ s s
)()作为 rc的函数，类似于图5‐a中所示的场景。
所有三条曲线都收敛于推论1给出的 2 n 。当 rc取值较小时，它们仍收敛于推
论1给出的 log 2 (n) n ≈ 0.009。注意，随着网络中汇聚点的数量增加，E[Λ s ( u]
Λ s s
)()减小。这是合理的，因为随着汇聚节点数量的增加，相应的路由树 数量也增加，因此其规模减小，最终导致节点转发的总流量负载降低。
图7‐{d,e,f}展示了终止时间 T(s)作为近似函数的每层分支数l
近似能量比 E(s) (ˆsE)，在与图5‐g类似的情景下，对于 k= 2, 3, 4分别取值的 情况。显然，当近似能量比的值较小时，终止时间可以显著增加。此外， 随着k的增大， T(s)的最大值也随之增大。这归因于当汇聚节点数量增加 时，能量空洞问题的影响得以减弱。

7. 结论

本文通过解析法研究和建模为设施选址问题，重新探讨了无线传感器 网络中的能耗问题。本文提出了一种解析模型，从理论上证明了当汇聚节 点根据 k‐中位数问题的解进行部署时，网络的总能耗最小化（即绿色使用）， 从而实现后续的网络寿命延长。此外，所给出的仿真结果验证了所提出的 解析模型，显示出在节能和网络寿命方面具有显著增益。