图和树（上）最小生成树-kruskal

最新推荐文章于 2025-11-19 18:24:27 发布

原创最新推荐文章于 2025-11-19 18:24:27 发布 · 114 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#kruskal #贪心算法

这篇博客介绍了如何运用Kruskal算法解决最小生成树问题，通过建立超级源点并构建图，实现寻找灌溉系统最经济方案。算法核心是按边权重排序并尝试合并不产生环的边，直至连接所有节点。

最小生成树 – kruskal

每次贪心的尝试将图中最小的非树边，标记为树边，非法则跳过

将全部边按照权值由小到大排序
按照顺序（边权由小到大）考虑每一条边，只要这条边和我们选择的边不构成环，就保留这条边，否则就放弃这条边
成功选择（n-1)条边后，形成一颗最小生成树秒如果无法选择出（n-1）条边，则说明原图不连通。

const int N = 50005;
const int M = 100005;
struct edge{
int u,v ,w;
bool operator < (const edge &t){return w < t.w;}
}e[M];
int n,m,rt;
int f[N];
void init(int n)
{ 
 for(int i = 1;i <=n;i++)
  f[i] = i;
}
int find(int x)
{
   retunr f[x] == x ? f[x] = find(f[x]);
}
bool unite(int x,int y)
{
  x = find(x);
  y = find(y);
  if(x==y) return false;
  f[x] = y;
  return true;
}
int kruskal_return_max()
{
  std::sort(e+1,e+1+m);
  int cnt = 0,ans=0;
  for(int i = 1;i <= m;++i)
  {
   if(unite(e[i].u,e[i].v))
    { ans = max(ans,e[i].w);
    if(++cnt == n-1) break;
    }   
  }
  return cnt == n-1 ? ans: -1;
}

问题描述
输入样例：
5 5 2
1 2 1
2 3 3
3 4 5
1 3 2
1 4 1
输出结果
8
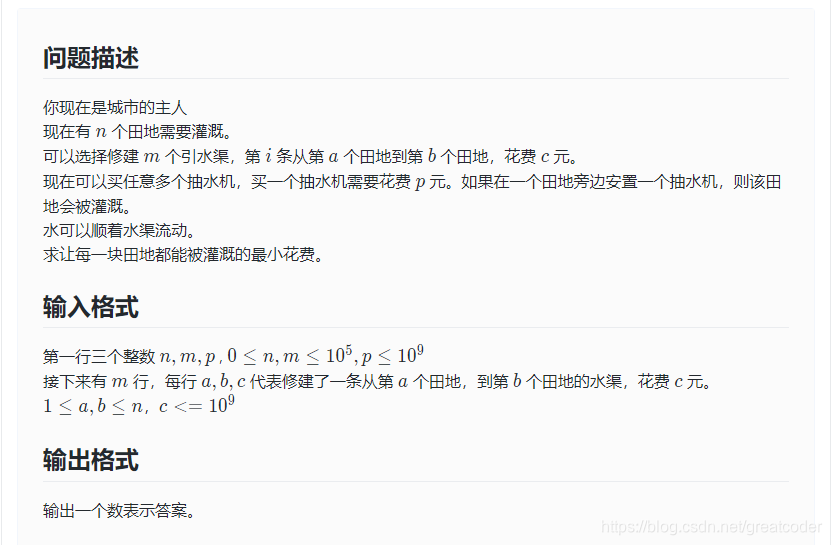
分析，因为每一块田都可以修建一个抽水机，且至少存在一个抽水机才有可能有水，我们设一个超级源点0，0点到所有点的距离都是p。ab之间有水渠，则建一条无向边，编边权为c。

#include<bits/stdc++.h>
using namespace std;
const int MAXN = 100005;

struct Edge{
    int u,v;
    long long w;
    bool operator<(const Edge &t) const
    {
        return w < t.w;
    }
}e[2*MAXN];

int tot,m,n;
int  head[MAXN];
bool vis[MAXN];
long long dis[MAXN];
int f[MAXN];

void init(int n)
{
    for(int i=0;i <= n ;i++)
        f[i] = i;
}

int find(int x)
{
    return f[x] == x ? x : f[x] = find(f[x]);
}

bool unite(int x,int y)
{
    x = find(x);
    y = find(y);
    if(x==y)
    return false;
    f[x] = y;
    return true;
}

long long kruskal()
{
    sort(e+1,e+1+n+m);
    int cnt = 0;
    long long ans = 0;
    for(int i=1;i <= n+m;i++ )
    {
        if(unite(e[i].u, e[i].v))
        {
            ans+=e[i].w;
            if(++cnt == n) break;
        }
    }
    return cnt == n ? ans : -1;
}


int main()
{
    //freopen("6_a.in","r",stdin);
    //freopen("6_a.out","w",stdout);
    long long p;
    cin>>n>>m>>p;
    //设0号点位超级源点
    //将零号点与所有点之间加以一条权值位p的边
    int i=0;
    init(n);
    for( i =1;i <=n;i++)
    {
        e[i].u = 0;
        e[i].v = i;
        e[i].w = p;
    }
    for(;i<=n+m;i++)
    {
        int a, b;
        long long c;
        cin>>a>>b>>c;
        e[i].u = a;
        e[i].v = b;
        e[i].w = c;
    }
    cout<<kruskal()<<endl;
    return 0;
}