基于LSTM的WSN节能数据挖掘

基于长短期记忆网络的深度学习在节能无线传感器网络中的分布式数据挖掘模型

1. 引言

一般来说，无线传感器网络（WSN）是一种自配置且无基础设施的无线网络，可用于监测外部环境和生态状况，例如温度、湿度、运动和污染物，并通过网络将信息传输至汇聚节点，以便对数据进行监控和预测。汇聚节点或基站（BS）被视为网络与用户之间的接口。通过使用此类网络，用户能够通过向基站发出查询来获取所需的关键数据。通常，一个无线传感器网络由大量传感器节点组成。这些传感器可通过无线电信号与交替节点进行通信。每个节点嵌入了处理单元、存储、无线收发器和电源元件。

单个WSN节点的计算速度、内存、通信带宽等资源均受限。一旦传感器节点被部署，它们需在系统内自行组织成适当的网络结构，并采用多跳通信过程。此外，无线传感器会响应来自“控制站点”的查询，仅处理特定规则和感知样本。可利用全球定位系统（GPS）以及本地定位技术来获取位置及相关信息。该网络通常限制使用执行器，执行器仅在特定情况下使用，因此有时也被称为无线传感器与执行器网络。

由于各种条件的存在，无线传感器网络（WSN）能够采用新技术并获取非常规的协议开发方法。为了实现最低复杂度和能量消耗以延长网络寿命，应在信号和数据计算能力之间找到适当的平衡。这有助于在科学事件中提供最大的能量支持。近年来，无线传感器网络领域在开发能量高效和计算高效的技術方面取得了多种进展，但该领域仍局限于简单的数据导向和报告功能。此外，提出了一种电缆模式转换（CMT）方法，用于计算活跃传感器节点的较低值，以平衡系统的K‐覆盖和K‐连通性。特别是，该方法根据本地数据确定非活动电缆传感器的时间段，使其在不影响网络覆盖和连接要求的情况下运行。

文献中提出了多种基于优化算法和深度学习（DL）模型的无线传感器网络操作节能解决方案。在Cheng等人[1],中，部署了一种延迟感知的无线传感器网络数据收集网络。其主要目标是减少无线传感器网络数据收集过程中的延迟，从而延长网络寿命。在Rahman和Matin[2],中，假设采用了更多数量的中继节点以降低网络脆弱性，同时应用粒子群优化(PSO)模型来针对中继节点确定优化的汇聚节点位置，以解决寿命问题。

无线传感器网络（WSN）的设计包含多个限制。最主要的限制是由于传感器节点被放置在恶劣环境中，且通常需要通过电池频繁充电。因此，与电池供电量以及节能方式相比，传感器寿命显著缩短。传感器功耗管理已成为一个活跃的研究领域。能量节约的目的应用于数据采集、计算、数据压缩、传输等[22‐24]。数据传输过程被认为是节省能量的第一步。因此，此类协议可以在通信中被视为不同的层，即物理层、MAC层、路由层以及应用层。在MAC层中，一旦发生碰撞，重新传输数据时会消耗大量能量，以及在没有有效数据或向相邻传感器节点发送探测包的情况下进行控制包传输。目前仅有少数协议被提出用于处理能耗问题。S‐MAC 协议 [3],采用来自传感器的时间同步，以循环方式进行隔离。

为了节省能耗并消除冲突，已部署PC‐MAC协议[4] 。在网络层，路由协议通过数据包传递机制来降低能耗。此外，它还试图利用无线传感器网络的高密度优势。开发新型无线传感器网络路由协议是一个极具前景的研究方向。根据所采用的机制，路由协议可分为地理位置中心、数据为中心、基于网络拓扑以及链路状态等类型。在数据为中心的协议中，GKAR被视为K选播协议的一个实例。EASPRP[5]寻找包含能效在内的最短路径，而EERT协议[6]则管理服务质量(QoS)。在实时应用中，REFER协议[7]采用Kautz图。只有部分路由协议可以组合使用，以覆盖特定区域。少数路由协议[8]利用移动传感器节点的移动能力。GAROUTE协议[9]利用遗传算法(GA)构建传感器组，以最小化通信。在此过程中，可部署簇头(CH)来计算局部信息并对相应数据进行分割。

LEACH协议是一种用于管理网络流量的成簇协议。它已被改进[10]，以提高传输时间并减少干扰。EEDR协议[11]主要集中传输数据包以降低能耗。已提出替代模型以最小化功耗并延长WSB的寿命。黄 J.‐W [12]跟随传感器覆盖主要用于减少能耗。相同的操作在[13]中重复应用，该模型采用了SCC（赞助覆盖计算）模拟模型。其他一些协议通过如SEPSen协议减轻数据传输[14] ，该协议在整个系统中应用数据处理。流量以及资源管理被利用在[15]中。主要类型的协议分别应用无线网络模拟器[16] 。

无线传感器网络（WSN）已被应用于多种场景，例如土地覆盖分类[17],车载系统中的SCR节点预测、故障分析、地下水质量评估[18]。传统上，此类应用有助于从融合中心确定样本数据。当WSN由大量传感器节点组成时，融合中心的硬件限制了采样数据的计算功能，而该硬件被认为成本较高且频繁升级较为复杂。因此，数据通信消耗了更多的能量，特别是对于无线中继节点而言。在过去十年中，数据挖掘（DM）方法被引入以从海量数据中获取有效数据，被认为是在预测大规模数据方面更高效的工具。

在过去几十年中，已提出诸如支持向量机（SVM）、提升法以及逻辑回归（LR）等浅层DM技术[19]。此外，通过应用这些浅层DM模型，虽然能够增强融合中心的功能，但能耗问题仍然未得到改善。解决这些问题的方法是将技术实现在传感器端以减少数据传输，但在WSN中执行这一方法更为繁琐。此外，欣顿和萨拉胡特迪诺夫[20]开发了一种名为深度神经网络（DNN）的深度数据挖掘技术，用于提取数据的内在表示并缓解数据维度问题。基于DNN的分布式机器学习模型已在[21]中提出。

尽管文献中已有多种模型，但需要注意的是，仍需提升无线传感器网络（WSN）的融合性能。同时，还需要实现最小能耗、信令开销和平均延迟，并获得最大吞吐量。由于存在大量传感器节点，无线传感器网络的样本数据迅速增长，导致融合中心的集中式数据挖掘方案面临降低融合中心负载以及减少整体能源利用的问题。鉴于此，本文提出了一种基于深度学习的分布式数据挖掘（DDM）模型结合LSTM以实现无线传感器网络融合中心的能效和最优负载均衡。所提出的分布式机器学习模型包含一个带有长短期记忆网络的循环神经网络（RNN‐LSTM）模型，该模型将网络划分为多个层并部署到传感器节点中。通过使用RNN‐LSTM模型，显著降低了无线传感器网络中融合中心的开销。同时，利用RNN‐LSTM模型传输数据所需的能量明显低于传输实际数据所需的能量。所提出的RNN‐LSTM模型在不同数量的隐藏层节点和信令间隔下进行了大量实验。实验结果表明，与其他方法相比，RNN‐LSTM降低了能耗、信令开销和平均延迟，并提高了整体吞吐量。本文贡献的优势如下所列。

a) 在不同领域中，无需通过手动过程对训练数据的标注数量进行要求，整个过程完全自动化。
b) 内部表示与交替的DM技术相结合，增强了模型以达到最优结果。
c) RNN‐LSTM的维度有助于减少无线传感器网络的数据传输，同时节约无线传感器网络的能量。
d) 分布式估计减少了融合中心的负载，从而带来诸多好处，如降低硬件需求和延迟。

本文的后续部分组织如下。第2节详细阐述了RNN‐LSTM模型。第3节对所提出模型的实验验证进行了验证，第4节总结了全文。

2. 提出的方法

所提出的用于分布式数据挖掘的RNN‐LSTM旨在实现无线传感器网络融合中心的能效和负载均衡。所提出的分布式模型包含一个带有长短期记忆网络的循环神经网络（RNN‐LSTM）模型，该模型将网络划分为多个层，并将其部署到传感器节点中。

2.1. 基本原理

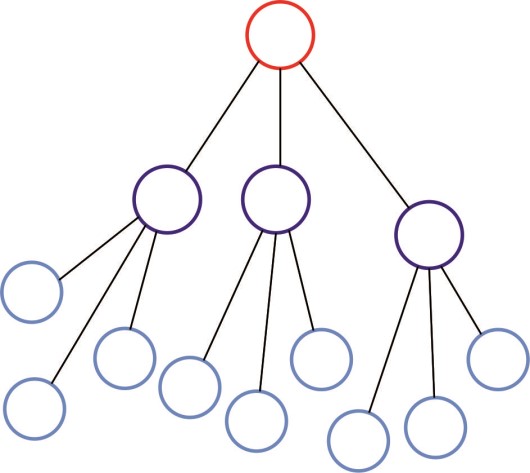
RNN‐LSTM模型的基本原理如下所述。假设存在一个具有融合中心的无线传感器网络，该网络被分为3个阶段（图1(a)）和三层RNN‐LSTM结构（图1(b)）。需要指出的是，无线传感器网络的拓扑结构与RNN‐LSTM的结构相同。

在层次结构中，有一种可能的解决方案，即将RNN‐LSTM划分为若干层，并分配到无线传感器网络的不同层级。图1(c)给出了将RNN‐LSTM划分为两部分并引入融合中心的示例。假设无线传感器网络已被划分为m个层级，而RNN‐LSTM包含n层。当将n层划分为k部分（k≤m, n）时，每一部分通过估算无线传感器网络中相应层级hu内的计算单元来实现，RNN‐LSTM的具体实现将在后续章节中说明。

步骤1 ：假设u= 1。传感器对实际数据进行采样，该数据由计算单元利用 RNN‐LSTM的初始部分从层级hi计算，并将仿真结果转发至层级hu+ 1的计算单元，以及u= u+ 1。

步骤2 ：估算从前一层级的计算单元获得的输入，如果u ≥ k，则转到步骤4。

步骤3 ：当 hu ≥ m 时，进入 步骤5。否则，返回 步骤2 并将结果传输到级别 hu+ 1、u= u+ 1 的计算单元。

步骤4 ：将数据转发至融合中心。

步骤5 ：分布式模型决策过程已完成。

2.2. RNN‐LSTM

LSTM方法被用于解决RNN梯度消失问题。它类似于标准的循环神经网络，并带有隐藏层，其中隐藏层的每个普通节点都可以被一个记忆单元替代，如图2所示。所有记忆单元都包含一条自连接递归边，以确保梯度能够多次传递而不会衰减。为了区分记忆单元与普通节点，使用了下标c作为记忆单元的标识。

术语“LSTM”源于即将出现的直觉。一个简单的循环神经网络在权重方面具有长期记忆，这种记忆在训练过程中逐渐改变，用于编码关于数据的通用知识。它还结合了短期记忆，以形成瞬态函数，该函数从每个节点传递到后续节点。这里，LSTM技术表示一种中间类型的记忆单元。记忆单元被视为一个复合元素，通过特定的连接过程由普通节点构成，并包含乘法节点，图中用字母Π表示。每个长短期记忆网络单元都经过枚举并定义如下：例如，s表示一个向量，在某一层的每个记忆单元c处取值为sc 。当下标c被使用时，它用于索引单个记忆单元。

• 输入节点 ：该单元被标记为gc，被认为是一个节点，它从当前时段的输入层l(z)以标准方式获得激活，同时也从过去时间步的隐藏层h(z−1)获得激活。通常，附加的权重输入是来自LSTM论文的tanh激活函数，且该激活函数用sigmoid表示。

• 输入门 ：门被认为是LSTM模型的独特特征。门类似于输入节点的sigmoid型函数，获取来自当前数据点l(z)以及过去时间步隐藏层的激活值。由于交替节点的相乘的值，该结构被称为门。如果该值被设为零，则称为门，此时交替节点的流被切断；当该值被设为一，则所有流均通过。此外，输入门uc的值会增加输入节点的值。

• 内部状态 ：所有记忆单元的核心点阳极 sc 包含线性激活，该线性激活在通用论文中被称为单元的内部状态。内部状态 sc 由具有恒定单位权重的自连接递归边构成。由于相邻时间步的边具有相似的权重，误差流在时间步之间流动时不会爆炸。这种现象被称为恒定误差环。对于向量函数，内部状态的更新为 s(z) = g(z) ⊙ u(z) + s(z−1)，其中 ⊙ 表示逐点乘法过程。

• 遗忘门 ：已经引入了fc门。它提供了一种模型来学习内部状态的上下文。它更适用于频繁运行的网络。使用遗忘门，前向传播中估计内部状态的函数为
  $$
  s(z) = g(z) \odot u(z) + f(z) \odot s(z−1)
  $$
  (1)

• 输出门 ：由记忆单元生成的值vc被视为内部状态sc的度量，该度量通过结果门oc的值增加。此外，通常内部状态通过tanh激活函数实现，因为它为每个细胞提供了与渐变tanh隐藏单元具有相似动态范围的仿真结果。但在替代的神经网络研究中，修正线性单元具有更高的动态范围，且易于训练。因此，对于可去除内部状态的非线性函数而言，这是合理的。

通常，输入节点被标记为g。我们沿用此惯例，但需注意这可能会引起混淆，因为g不接受gate。在原始论文中，门被称为yin和yout，但这容易产生混淆，因为在机器学习文献中 y通常表示输出。为了提高可理解性，我们打破这一惯例，分别使用u、f和o来表示输入门、遗忘门和输出门。

在LSTM被提出后，出现了许多变体。遗忘门（如前所述）于2000年被提出，并不属于最初提出的原始LSTM的一部分。然而，它们已被证实非常有效，并成为大多数当前实现中的标准组件。窥视孔连接是指从内部状态直接传递到同一节点的输入门和输出门的连接，而无需主要依赖输出门进行调整。这些细节表明，此类连接能够提升网络在时序任务上的表现，其中网络需要学习测量测量之间的精确间隔。窥视孔连接的直观思想可通过以下示例说明：假设一个网络需要学习计算物体数量，并在看到n个物体后输出相应结果。该网络可能会发现，每次看到一个物体后，向内部状态中添加适当数量的激活值是可行的。这些激活值通过恒定误差环保存在内部状态 sc中，并在每次看到新物体时迭代累加。当看到n个物体时，网络需要判断何时从内部状态释放内容，以便将其纳入输出。为了实现这一点，输出门oc必须了解内部状态sc的满足情况，因此sc必须作为 oc的输入。LSTM结构中的计算基于记忆机制。

细胞并正确设置。后续计算在每个时间步长执行。这些方程提供了带有遗忘门的最新长短期记忆网络的完整技术：
$$
g(z) = \phi(W_{gl}l(z) + W_{gh}h(z−1) + b_g)
$$
$$
u(z) = \sigma(W_{ul}l(t) + W_{uh}h(z−1) + b_u)
$$
$$
f(z) = \sigma(W_{fl}l(t) + W_{fh}h(z−1) + b_f)
$$
$$
o(z) = \sigma(W_{ol}l(t) + W_{oh}h(z−1) + b_o)
$$
$$
s(z) = g(z) \odot u(u) + s(z−1) \odot f(t)
$$
$$
h(z) = \phi(s(z)) \odot o(t)
$$

在时间z ，长短期记忆网络隐藏层的值是向量h(z)，其中h(z−1)是隐藏层中每个记忆单元在前一时刻的输出值。考虑这些方程包含遗忘门，尽管没有窥视孔连接。不带遗忘门的简化长短期记忆网络的计算可通过将f(z)= 1设置为每个z来实现。我们使用tanh函数φ作为输入节点g，遵循现代设计。但是，在LSTM论文中，g的激活函数是 sigmoidσ。

自发地，在前向传播过程中，如果允许激活进入内部状态，则LSTM会被学习。当输入门获得值0时，不会包含任何激活。同样，输出门会学习何时释放值。如果两个门都关闭，则激活被保留在记忆单元中，既不会增加也不会减少，也不会干扰中间时间步的输出。在反向传播过程中，恒定误差环允许梯度在多个时间步之间向后传播，既不会爆炸也不会消失。从这个意义上讲，门在学习何时允许误差流入，以及何时将其释放。实践中，LSTM表现出比简单循环神经网络更强的学习长距离依赖的能力。因此，本综述所涵盖的现代应用论文普遍采用LSTM方法。

一个反复出现的困惑在于，多个记忆单元被共同用于包含工作神经网络的隐藏层。每个记忆单元的输出在下一步时间步中流向输入节点，并进入所有记忆单元的各个门。通常包含多层记忆单元。通常，在这些设计中，每一层从同一时间步的下一层以及前一个时间步的相同层获取输入。

2.3. 训练

训练分布式RNN‐LSTM

通过将RNN‐LSTM应用于分布式模型，需要在初始阶段于融合中心训练 RNN‐LSTM。训练数据来自每个无线传感器网络传感器的实例，训练后的 RNN‐LSTM参数被发送到分配在各个计算单元中的RNN‐LSTM层。当无线传感器网络提供大量训练数据时，这些数据也会消耗大量网络能量。事实上，传感器的实例数据在短时间内不会发生变化。因此，可选择其中一个实例来训练RNN‐LSTM。问题在于我们无法确定数据是否发生了变化。一种随机选择技术已被验证有助于解决此问题，一项数字标识探索表明，采用10%训练的随机选择可获得更好的输出结果。因此，该随机选择技术能有效减少需广播的冗余数据量。

随后，我们通过随机选择技术提供训练过程，如下所述。

1. 融合中心任意创建一个传感器的ID并向该传感器发送请求。
2. 选定的传感器接收请求并传输实例数据。
3. 融合中心从选定的传感器获取训练数据，并将数据传输至GLT技术。
4. GLT技术判断训练输出是否达到停止状态。若为是，则进入步骤5；否则，返回步骤1。
5. 融合中心将RNN‐LSTM结构数据的全部部分传输给相应的计算单元。

RNN‐LSTM的分布层次基于其功能。但某些分布层次必须结合功耗进行控制。规划分布层次的原则取决于计算和广播功耗之间的权衡。假设存在一个计算单元，它执行c次训练以完成分布式模型角色。所有训练消耗Ei功率。此外，该计算单元在无任何影响和衰减的情况下向目标节点发送1比特数据消耗Et功率。每次有干扰影响时衰减效应会导致 Eo的功耗进一步增加。接下来声明，当满足以下公式时，允许计算单元使用RNN‐LSTM部分：
$$
cE_i \leq (b_i - b_o)(E_t + E_o),
$$
(3)
其中bi是计算单元输入的比特大小，bo是计算单元输出的比特大小，bi ≥ b。如果Eo被设置为0，则接下来我们包含
$$
\frac{c}{b_i - b_o} \leq \frac{E_t}{E_i}
$$
(4)

值得注意的是，当公式(4)满足时，公式(3)也应同时满足。事实上，公式(4)是一个传统约束，它解决了计算单元所获得的计算上限角色。

3. 实验验证

为了验证RNN‐LSTM模型在WSN中用于分布式数据挖掘的结果，在MATLAB R2014a中进行了一组实验。此处，通过改变隐藏层节点数量和信令间隔来验证结果。隐藏层节点数量范围为5到40，信令间隔介于240至260之间。用于分析性能的指标包括信令开销、平均吞吐量和平均延迟。同时还与OSPF和DNN模型进行了对比分析。

3.1. 隐藏层节点数量变化下的结果分析

在本节中，从信令开销、平均吞吐量和平均延迟方面验证了RNN‐LSTM模型在隐藏层节点数量变化下的性能。

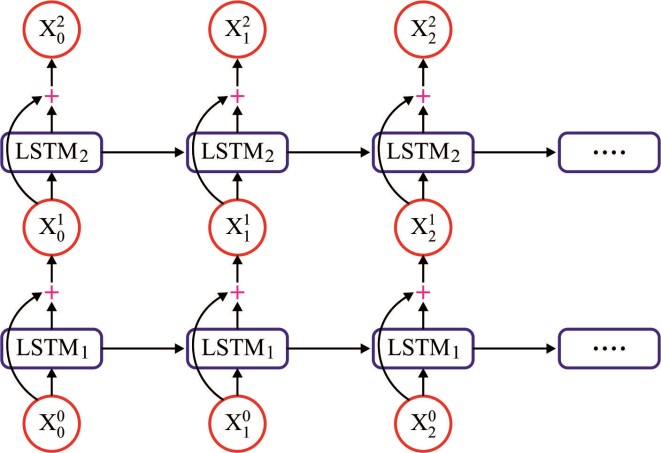
图3研究了RNN‐LSTM和其他模型在信令开销方面的结果。该图表明，RNN‐LSTM模型通过实现最低的信令开销表现出有效结果。与此同时，DNN模型相比RNN‐LSTM显示出较高的信令开销，而OSPF模型则表现出最差性能，在比较方法中信令开销最大。

例如，在存在5个隐藏层节点的情况下，RNN‐LSTM的信令开销最小值为28，而OSPF和DNN模型的信令开销最大值分别为120和34。例如，在存在20个隐藏层节点的情况下，RNN‐LSTM的信令开销最小值为28，而OSPF和DNN模型的信令开销最大值分别为113和34。例如，在存在30个隐藏层节点的情况下，RNN‐LSTM的信令开销最小值为29，而OSPF和DNN模型的信令开销最大值分别为107和35。例如，在存在40个隐藏层节点的情况下，RNN‐LSTM的信令开销最小值为30，而OSPF和DNN模型的信令开销最大值分别为102和35。

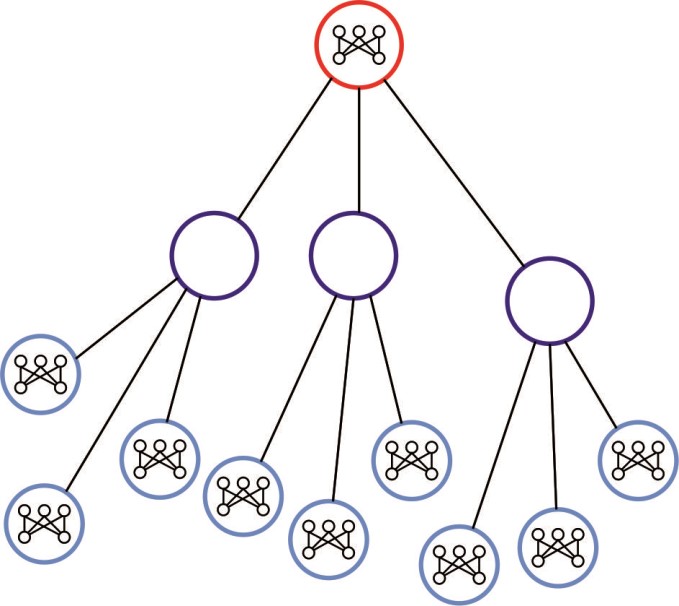
图4展示了RNN‐LSTM和其他模型在平均吞吐量方面的输出结果。该图表明，RNN‐LSTM模型通过提供最大吞吐量表现出更优的性能。与此同时，DNN模型相较于RNN‐LSTM表现出中等平均吞吐量，而OSPF模型则表现较差，在比较方法中提供的吞吐量最低。

例如，在存在10个隐藏层节点的情况下，RNN‐LSTM可实现1.39Gbps的最大吞吐量，而OSPF和DNN模型的吞吐量分别略低，为1.35Gbps。例如，在存在20个隐藏层节点的情况下，RNN‐LSTM可实现1.68Gbps的最大吞吐量，而OSPF和DNN模型的吞吐量分别略低，为1.52Gbps和1.6Gbps。例如，在存在30个隐藏层节点的情况下，RNN‐LSTM可实现1.9Gbps的最大吞吐量，而OSPF和DNN模型的吞吐量分别略低，为1.6Gbps和1.8Gbps。例如，在存在40个隐藏层节点的情况下，RNN‐LSTM可实现2.1Gbps的最大吞吐量，而OSPF和DNN模型的吞吐量分别略低，为1.7Gbps和1.92Gbps。

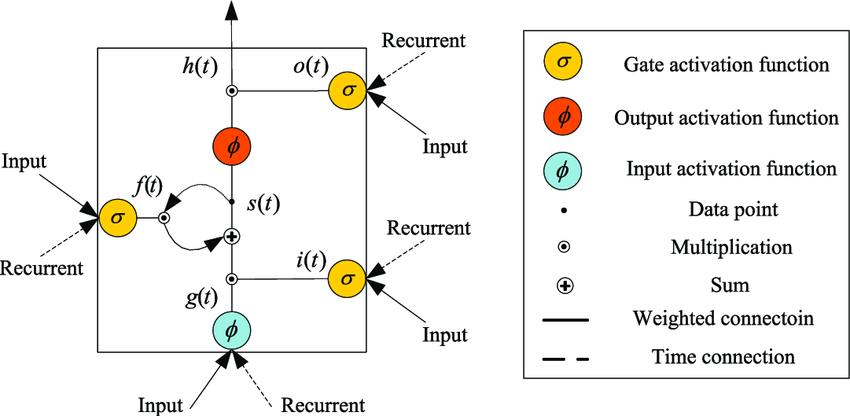
图5展示了RNN‐LSTM和其他模型在平均延迟方面的结果。该图表明，RNN‐LSTM模型通过实现最小平均延迟表现出有效结果。同时，DNN模型相比RNN‐LSTM显示出较高的平均延迟，而OSPF模型则表现出最差性能，在比较方法中提供了最大平均延迟。

例如，在存在5个隐藏层节点的情况下，可以看出RNN‐LSTM实现了220毫秒的最小平均延迟，而OSPF和DNN模型的平均延迟分别为235毫秒。例如，在存在20个隐藏层节点的情况下，可以看出RNN‐LSTM实现了222毫秒的最小平均延迟，而OSPF和DNN模型的平均延迟分别为242毫秒和236毫秒。例如，在存在30个隐藏层节点的情况下，可以看出RNN‐LSTM实现了222毫秒的最小平均延迟，而OSPF和DNN模型的平均延迟分别为570毫秒和236毫秒。例如，在存在40个隐藏层节点的情况下，可以看出RNN‐LSTM实现了222毫秒的最小平均延迟，而OSPF和DNN模型的平均延迟分别为690毫秒和236毫秒。

3.2. 信令间隔数量变化下的结果分析

在本节中，针对信令开销、平均吞吐量和平均延迟，验证了RNN‐LSTM模型在不同信令间隔下的输出结果。

图6考察了RNN‐LSTM和其他模型在不同信令间隔下的信令开销方面所达到的结果。结果表明，RNN‐LSTM模型表现出卓越的性能，在不同信令间隔下相比比较方法提供了最小的信令开销。

例如，在260毫秒的信令间隔下，RNN‐LSTM的信令开销最小为17，而OSPF和DNN模型的信令开销最大分别为120和20。例如，在250毫秒的信令间隔下，RNN‐LSTM的信令开销最小为18，而OSPF和DNN模型的信令开销最大分别为125和30。例如，在240毫秒的信令间隔下，RNN‐LSTM的信令开销最小为19，而OSPF和DNN模型的信令开销最大分别为130和33。

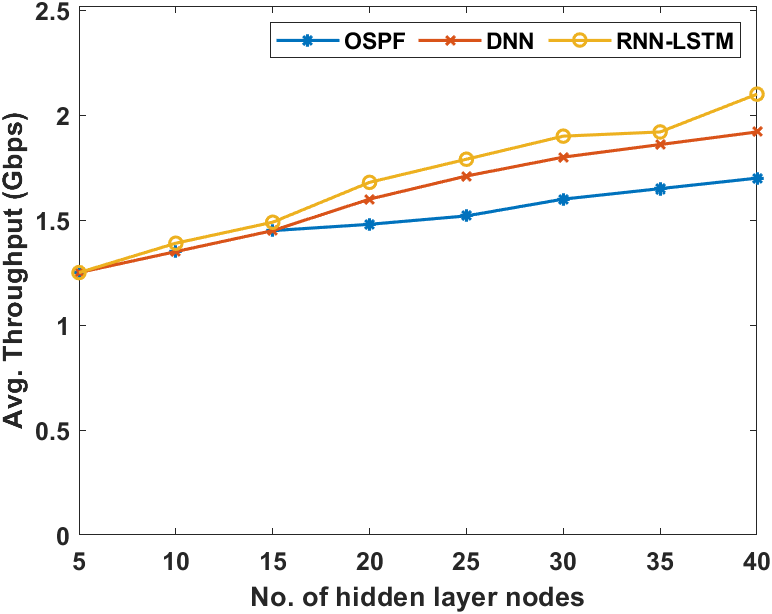
图7展示了RNN‐LSTM模型及其他模型在不同信令间隔下的平均吞吐量输出结果。该图表明，RNN‐LSTM模型在所有应用的信令间隔下均能提供最大吞吐量，表现出更优的性能。

例如，在260毫秒的信令间隔下，RNN‐LSTM的最大吞吐量达到1.336Gbps，而OSPF和DNN模型的吞吐量分别略低，为1.334Gbps和1.335Gbps。在250毫秒的信令间隔下，RNN‐LSTM的最大吞吐量达到1.3365Gbps，而OSPF和DNN模型的吞吐量分别略低，为1.334Gbps和1.334Gbps。在240毫秒的信令间隔下，RNN‐LSTM的最大吞吐量达到1.337Gbps，而OSPF和DNN模型的吞吐量分别略低，为1.321Gbps和1.3345Gbps。

图8展示了RNN‐LSTM和其他模型在不同信令间隔下的平均延迟方面的结果。该图表明，RNN‐LSTM模型通过在不同信令间隔下实现最小平均延迟，表现出有效结果。例如，在260ms的信令间隔下，可以看出RNN‐LSTM实现了180毫秒的最小平均延迟，而OSPF和DNN模型的平均延迟分别为200毫秒和210毫秒。例如，在250ms的信令间隔下，可以看出RNN‐LSTM实现了185毫秒的最小平均延迟，而OSPF和DNN模型的平均延迟分别为220毫秒和225毫秒。例如，在240ms的信令间隔下，可以看出RNN‐LSTM实现了190毫秒的最小平均延迟，而OSPF和DNN模型的平均延迟分别为230毫秒和230毫秒。

通过查看上述图表可以明显看出，与RNN‐LSTM相比，DNN模型表现出较高的信令开销，而OSPF模型在所有比较方法中信令开销最大，表现出最差性能。同时，与RNN‐LSTM相比，DNN模型表现出中等平均吞吐量，而OSPF模型提供的吞吐量最低，在比较方法中性能最差。此外，还观察到RNN‐LSTM模型传输数据所需的能量明显低于传输实际数据所需的能量。仿真结果表明，与其他方法相比，RNN‐LSTM降低了信令开销和平均延迟，并最大化了整体吞吐量。

4. 结论

本研究开发了一种新的用于无线传感器网络中分布式数据挖掘的RNN‐LSTM模型，以实现无线传感器网络融合中心的能效和最优负载均衡。通过使用RNN‐LSTM模型，大大降低了无线传感器网络融合中心的开销。同时，RNN‐LSTM模型在处理后数据传输中的能耗明显低于实际数据的传输。此处的结果是在不同数量的隐藏层节点和信令间隔下验证的。隐藏层节点的数量范围为5到40，信令间隔介于240‐260之间。用于分析性能的指标包括信令开销、平均吞吐量和平均延迟。同时，RNN‐LSTM模型传输数据所需的能量明显低于传输实际数据所需的能量。仿真结果表明，与其他方法相比，RNN‐LSTM降低了信令开销和平均延迟，并最大化了整体吞吐量。值得注意的是，在240毫秒的信令间隔下，RNN‐LSTM可实现最低190毫秒的平均延迟，而OSPF和DNN模型的平均延迟分别为230毫秒和230毫秒。未来，可以通过采用超参数调优技术进一步提升所提出模型的性能。