第十三章 原理篇：SWIN-transformer

参考教程：
swin-transformer/model.py
SWIN-Transformer: Hierarchical Vision Transformer using Shifted Windows

概述

在前面介绍了vision transformer的原理，加入transformer的结构后，这种网络在多种图像任务中都取得了不错的结果。但是它也存在一些问题。

第一个问题就是上一章提过的粗粒度问题，patch的大小比较大时，一个patch内可能有多个相似特征。

第二个问题就是当你想获得更多的特征时，就必须使用很长的序列。这里的序列长度指的是N*D中的N。想要获得更多的N，patch的大小就需要变小，也就是更加细粒度。但是这种情况下，在计算内积的时候就效率很低，尤其考虑到encoder的block要反复做很多次，速度就更慢了。

上图可以看出swin-transformer和vit有着比较明显的区别。首先siwn有着层次化的结构，随着层数加深，特征图的大小是在变化的。在VIT中，假如你将原始图片分割成16x16的patch，那么从始至终你的patch的大小都是固定的，而在swin中你能看出你的patch的大小有一个4*4->8*8->16*16的变化。其次是swing的特征图中有很多的划分好的名为窗口的区域，这也是它的方法的核心，VIT中所有的patch之间都要进行self-attention的计算，而swin中只在窗口内进行计算，这样计算量也会大大减小。

swin-transformer使用窗口和分层的方式。为了把结果做的比较好，第一层用很细粒度的token，在后面的层里为了提高效率，开始进行token的合并。经过每一层合并，token的数量会越来越少，计算量也会相对的减少。

token数量逐渐降低，就像卷积网络中feature map逐渐减小的过程。swin-transformer其实就是模拟了CNN的过程，随着层次的加深，token的数量降低，但是embedding_dim按层翻倍。

看整个流程，本质上还是一样的。首先对输入的图像进行编码。这里使用的是patch partition, 获得H/4*W/4个embedding，embedding_dim = 4*4*3 = 48。

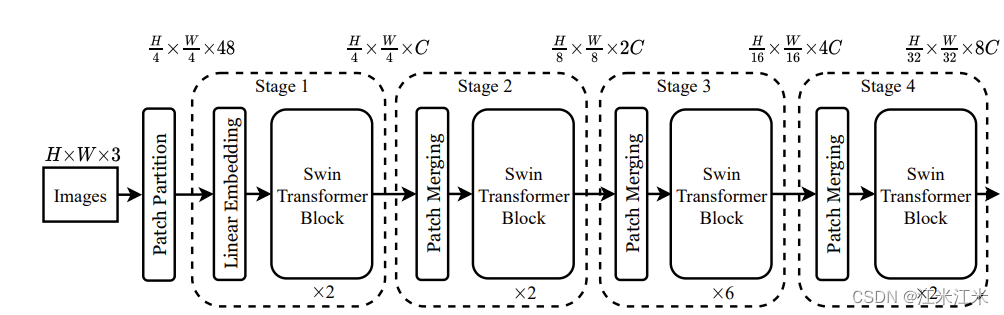
之后开始在网络中进行一层一层的forward。并且隔几个block进行一次patch merging。patch merging的作用就是将patch合并在一起，减少patch的数量。

在这个网络中，使用的block就是swin-transformer block，也就是shifted windows transformer，基于滑动窗口的方法。作者提出了滑动窗口这个机制，它不仅限制了没有重叠的窗口的自注意力计算，也允许跨窗口的连接。这样窗口内部和窗口之间都会存在信息传递。

综合来说，它的整体架构还是可以分成两部分：

1. 得到pacth。
2. 分层计算attention

transformer blocks

swin transformer block 和VIT中transformer block的主要区别就是用一个基于shifted window计算的多头自注意力模块取代了标准的MSA。
那么基于窗口的MSA做了哪些工作呢？
swin使用窗口，把一个图像分成一块一块不重叠的区域。假设每一个窗口包含M*M的patch。那么对于一个拥有h*w个patch的图像，MSA和W-MSA的计算量会有很大的差别。
$$\begin{array}{r}\Omega (MSA)=4hw{C}^2+2(hw{)}^{2}C\\ \Omega (W-MSA)=4hw{C}^2+2M^{2}hwC\end{array}$$
在h和w很大的时候，global的自注意力的计算量是难以负担的，但是基于窗口的自注意力下，计算量就比较容易接受。

计算量

来看一下这个计算量是如何计算得到的。

1. 对于MSA：
   1. C代表着我们的token的维度，假设我们的输入大小为$A^{h\ast w,C}$，在进行Q\K\V的计算时维度没有发生变化，那么我们计算$A^{h\ast w,C}\ast W^{C,C}$的矩阵乘法的过程中，每次计算的计算量是$hw{C}^2$
   2. 因为Q\K\V计算了三次，所以三次的计算量为$3hw{C}^2$。
   3. 下一步是计算$Q^{h\ast w,C}$和$K^{h\ast w,C}$的内积，计算结果为$X^{h\ast w,h\ast w}$，内积计算需要点对点进行计算，所以计算量为$h^2{w}^{2}C$。
   4. 再下一步计算$X^{h\ast w,h\ast w}\ast V^{h\ast w,C}$，计算量为$h^2{w}^{2}C$。
   5. 因为这里是多头的自注意力机制，所以还需要增加一步$B^{h\ast w,C}\ast W^{C,C}$，计算量为$hwC$
   6. 所以对h*w个patch做MSA，总的计算量加起来为$4hw{C}^2+2h^2{w}^{2}C$
2. 对于W-MSA:
   假如窗口大小为M*M，那么在W-MSA中窗口数量为$\frac{h}{M}\ast \frac{w}{M}$
   1. 对M*M个patch做MSA，总的计算量是$4M^2{C}^2+2M^{4}C$
   2. 一共要进行$\frac{h}{M}\ast$