决策规划（五）---动态规划

笔记来自 B 站

1.路径决策

以 host(ego) 在 reference line 的投影为坐标原点，建立 frenet 坐标系
找到规划起点：
为了保证控制的连续性，规划的起点为 t+T 时刻
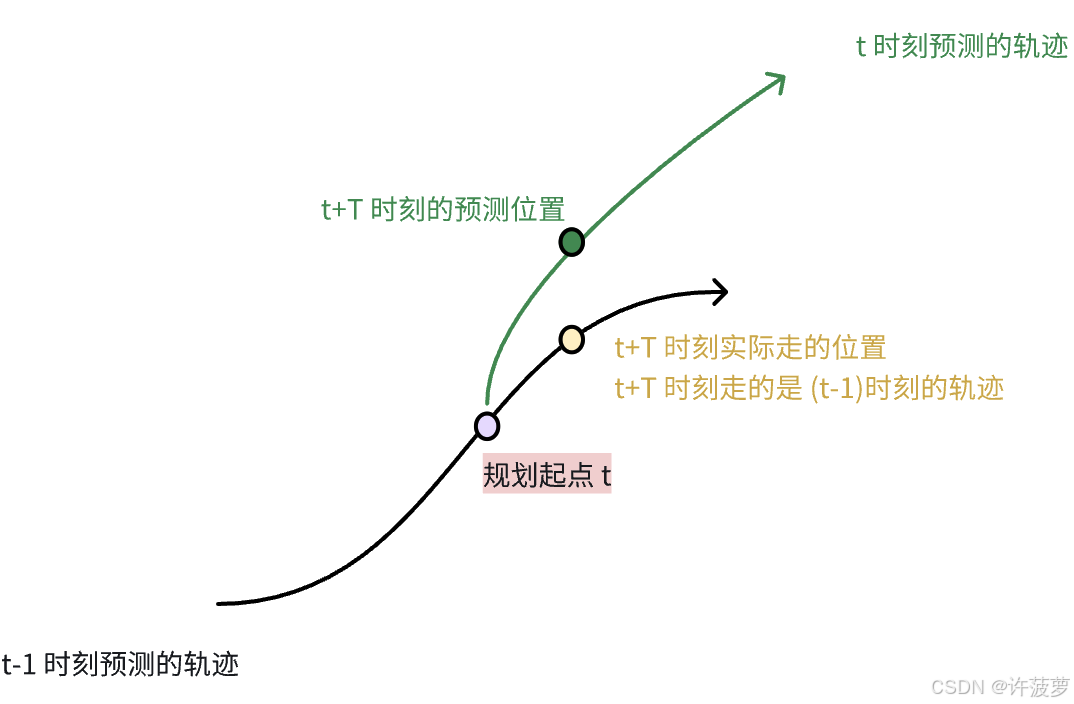
如下图所示，如果规划起点选择在 t 时间的点，绿色的线为 t 时刻预测的轨迹，在 t+T 时刻自车应该在绿色点的位置。但是，控制在 t 时刻拿到的是 (t-1) 时刻的轨迹，在 t+T 时刻控制随着 (t-1) 时刻的轨迹走到黄色的点，这就造成了控制的不连续性

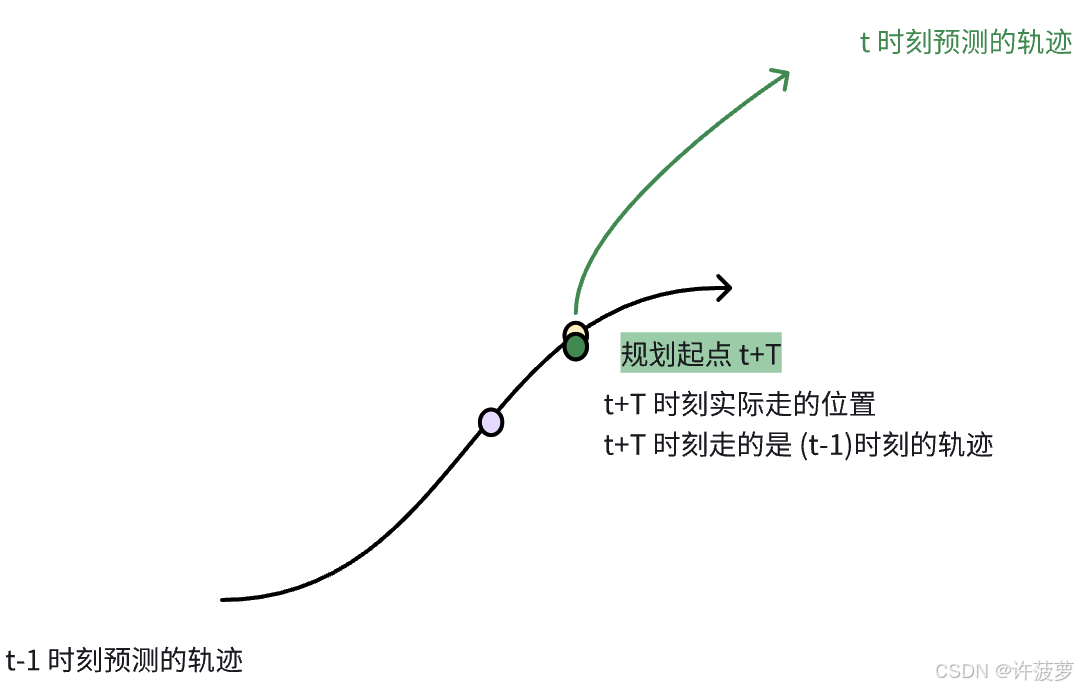
如下图所示，规划的起点在 t+T 时刻，控制还是走 (t-1) 时刻的轨迹，那么在 t+T 时刻，规划的轨迹和控制走的点是一样的，所以 t 时刻规划的起点要是 t+T 时刻

2.寻找最优路径标准

最优路径标准：平滑，与障碍物保持适当距离，贴近参考线，下图中这条粉色的线就没有贴近参考线

有障碍物的二次规划是非凸的，如下图所示，这个车有多重方法可以绕过这个树：

代价函数如下图所示，代价函数值最大的位置就是代价函数最大的地方：

2.1 撒点法

每隔一定的米数撒一些点，寻找每个点的最优路径，这个路径就叫粗径：

然后基于这些粗径进行第二次的规划，解出一条最优路径：

如何在离散空间上找到粗解：动态规划
如何在凸空间上优化出最终解：二次规划

3.动态规划

3.1 计算每个路径的代价函数

如何判断生成轨迹的质量，需要用到代价函数：

平滑代价解释：
s 代表弧长，期望弧长越平滑越小，但是对该期望求积分比较困难，所以就简化为每个离散点的积分

障碍物距离代价：
相当与对障碍物画了两个圈，外圈是 d1，内圈是 d2 ，当在 (0,d2) 范围内接近于无穷大

最终就可以求出每个起点终点的最短路径

3.2 找到最短路径

可以使用迪杰斯特拉算法求出图的最短路径，也可以使用动态规划的方式：
现在要计算出 P0 —> P12 or P22 or P32 哪种代价最小，笨方法是计算
P0–>P12，计算 P0—>P22。。。
但是动态规划可以先将 P0—>P11 ，P0—>P21 ，P0—>P31 的结果进行保存然后再计算计算后面的结果，这样就减去了一部分计算量

4.轻决策与轻决策

为什么不使用粗规划（动态规划）的结果作为最终结果：因为粗规划是使用离散撒点的方式找到最优路径，撒点的方式本身就不是最优解
动态规划是一种决策的手段，相当于找到一段凸空间，然后再从这个凸空间中进行二次规划找到最优路径
二次规划是一个五次多项式，约束可以写成下图：

动态规划与决策的关系

4.1 重决策

为什么人为给定的空间有可能是非凸空间：
下面的两个蓝色的框是障碍物，人为可能会规划的空间是非凸空间

重决策优点：

4.2 轻决策

轻决策缺点：

4.3 重决策与轻决策的应用