1.对撞指针
在头部和尾部分别设置一个指针,一个指针向后移动一个指针向前移动,如果指针对撞则停止循环
344 反转字符串
算法描述
start 从前向后, end 指针从后向前,交换两个指针指向的元素
代码实现
class Solution {
public:
void fanzhuan(vector<char>&s,int start,int end){
while(start<end){
swap(s[start++],s[end--]);
}
}
void reverseString(vector<char>& s) {
fanzhuan(s,0,s.size()-1);
}
};
时空复杂度
时间复杂度:O(N)
空间复杂度:O(1)
167 两数之和-输入有序数组
class Solution:
def twoSum(self, numbers: List[int], target: int) -> List[int]:
n = len(numbers)
i = 0
j = n - 1
while i < j:
if numbers[i] + numbers[j] == target:
return [i+1, j+1]
elif numbers[i] + numbers[j] > target:
j -= 1
else:
i += 1
return [i+1,j+1]
125 判断字符串是否回文
class Solution:
def twoSum(self, numbers: List[int], target: int) -> List[int]:
n = len(numbers)
i = 0
j = n - 1
while i < j:
if numbers[i] + numbers[j] == target:
return [i+1, j+1]
elif numbers[i] + numbers[j] > target:
j -= 1
else:
i += 1
return [i+1,j+1]
字符串涉及方法:
# 转换成大写
upper()
# 转换成小写
lower()
# 判断是否是字母或者数字
isalnum()
# 转换成大写 upper() # 转换成小写 lower() # 判断是否是字母或者数字 isalnum()
11 盛最多水的容器
class Solution:
def maxArea(self, height: List[int]) -> int:
max_v = 0
i = 0
j = len(height)-1
while i<j:
# 先计算当前面积
volumn = (j-i)*min(height[i],height[j])
max_v = max(max_v,volumn)
#移动那根较短的柱子
if height[i]<height[j]:
i+=1
else:
j-=1
return max_v
先计算再移动
判断大小涉及方法
# 判断两个数谁更小 min(a,b) # 判断两个数谁更大 max(a,b)
344 翻转字符串
class Solution:
def reverseString(self, s: List[str]) -> None:
"""
Do not return anything, modify s in-place instead.
"""
i = 0
j = len(s)-1
while i<j :
s[i],s[j] = s[j],s[i]
i+=1
j-=1
345-翻转字符串的元音字母
class Solution:
def reverseVowels(self, s: str) -> str:
array = ['a', 'e', 'i', 'o', 'u', 'A', 'E', 'I', 'O', 'U'] # 定义元音
s_list = list(s) # str 2 list ,因为 str 没有 not in 和 in 方法
i, j = 0, len(s)-1
while i < j:
if s_list[i] in array and s_list[j] in array:
s_list[i], s_list[j] = s_list[j], s_list[i]
i += 1
j -= 1
if s_list[j] not in array:
j -= 1
if s_list[i] not in array:
i += 1
return ''.join(s_list) # list 2 str
字符串转换相关方法
# 字符串转换成 list list(s) # list 转换成字符串 ‘’.join(s_list)
15三数之和(media)
2.7.1算法描述
1.什么时候可以对 nums 进行排序
这里我们返回的是 nums 中的值而不是 nums 中某几个元素的 index ,所以我们可以将 nums 进行排序然后再加以判断。
如果题目中要求返回 nums 的 index ,则无法打乱 nums ,或者先将 nums 的下标进行保存
2.步骤:
如果使用 for 循环的话需要使用三重 for 循环,但是也可以使用滑动窗口实现
需要对 nums 中的每一个元素进行判断。假设说现在判断 -4 这个元素
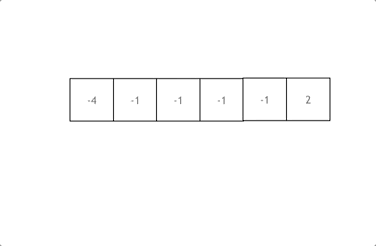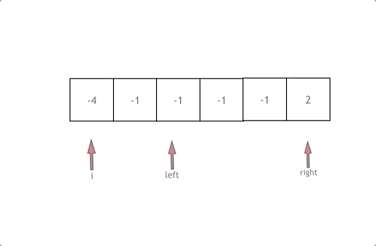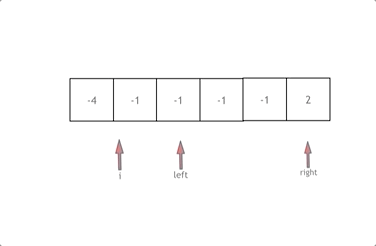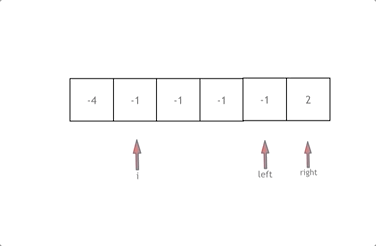
cur = -4 在这一轮循环中这个值就固定了,就要计算 cur 和它滑动窗口中的和
left 为 cur 右边第一个元素,right 为最后一个元素
将 cur ,left,right 的值相加,如果 sums <0 ,left 向右移动,如果 sums >0 right 向左移动
当 sums==0 时:
这个时候 cur 还没有判断完,滑动窗口中满足 sums 的 left 和 right 可能不止一个,所以还要继续移动 left ,right ;与此同时避免 left ,right 相邻重复的情况
3.在进行滑动窗口计算时先要判断:
①这个 cur 在刚才是否有判断过
②cur 的值是否>0,因为 nums 是顺序排序的,如果 cur>0 则后面不用再判断
4.技巧
三数之和可以使用固定一个值然后再滑动窗口的方式求和,减少 for 循环
易错点:
left 和 right 的去重操作
(1)在 i ,left,right 的值不满足taget 的时候是不用进行去重操作的,因为 nums[left],nums[right] 的值不会被放入 path 中,所以不用去重
(2)当 sums 的值等于 target 时就要进行去重操作,去重到下一个数和当前数不相等为止。去重的方式有很多
2.7.2 C++ & Python 代码实现
1.C++ 代码实现
class Solution {
public:
vector<vector<int>> threeSum(vector<int>& nums) {
vector<vector<int>> res;
sort(nums.begin(),nums.end());
for(int i =0;i<nums.size();i++){
if(nums[i]>0) break; // 因为顺序了,如果 i 指向的元素>0 则不用接着判断了
if(i>0&&nums[i]==nums[i-1]) continue; // i 元素也要去重
int left = i+1;
int right = nums.size()-1;
while(left<right){
int sums = nums[left]+nums[right]+nums[i];
if(sums==0){
res.push_back(vector<int>{nums[i],nums[left],nums[right]});
// left,right 指向的元素不能立刻移动,也要去重
while(left<right&&nums[right]==nums[right-1]) right--;
while(left<right&&nums[left]==nums[left+1]) left++;
// 通过上一步 while 循环指向的还是重复值所以继续进行下一步收缩
right--;
left++;
}else if(sums>0) right--;
else left++;
}
}
return res;
}
};
2.Python 代码实现
class Solution:
def threeSum(self, nums: List[int]) -> List[List[int]]:
res = []
n = len(nums)
nums = sorted(nums)
for i in range(n): # 逐个遍历 nums 中的每个元素
left = i+1
right = n-1
if nums[i]>0: # nums 已经排序,右边的都是比它大的。left right 都是从它右边开始判断
break
if i>=1 and nums[i]==nums[i-1]:# 为了防止出现结果一样的情况
continue
while left<right:
sums = nums[i]+nums[left]+nums[right]
if sums<0:
left+=1
elif sums>0:
right-=1
else:
res.append([nums[i],nums[left],nums[right]])
# 这时候 cur 的判断还没有结束,后面也许还有能满足条件 left 和 right
# left 和 right 也要跳过相等的值
while left<right and nums[left] == nums[left+1]:
left+=1
while left<right and nums[right] == nums[right-1]:
right-=1
left+=1
right-=1
return res
错误代码
class Solution:
def threeSum(self, nums: List[int]) -> List[List[int]]:
n = len(nums)
if n<3:
return []
res = set()
for i in range(0,n-2,1):
for j in range(i+1,n-1,1):
for k in range(j+1,n,1):
if (nums[i]+nums[j]+nums[k])==0:
res.add((nums[i],nums[j],nums[k]))
return list(res)
这里不可以使用三重 for 循环计算值与之之间的和,然后保存到 Set 中,因为会出现下面重复的输出。而去重操作比较费时所以不建议这个方法

2.7.3 时空复杂度
时间复杂度:O(N²)
空间复杂度:O(N)
18 四数之和
2.8.1 算法描述
三数之和的解法是一层 for 循环中嵌套一个 while 循环,for 循环固定 nums[i] ,while 循环移动 left ,right
四数之和的解法是两层 for 循环,一层固定 nums[i] ,另一层固定 nums[j],在这两者都固定的情况下移动 left 和 right 的位置
如果有五个数组的话那就使用 3 层 for 循环,几层 for 循环就要有几个数组,然后减掉滑动窗口的两个指针即可
如何避免有重复的值产生:
i,j,left,right 都要判断它们的后一个值是否与当前值相同,如果相同的话就要 continue ,因为在这种情况下产生的结果是一样的
同样 left,right 指针也要再加一个判断,防止下一步还是指向相同的位置
易错点:
1.这里的 target 是任意值不能通过 nums[i]>target 就进行剪枝,所以这里只进行去重操作
2.这里对 j 进行去重时因为 j 是从 i+1 开始的,在判断 nums[j-1] 和 nums[j] 是否相等时 ,j 的范围是 j>i+1
3.这里不能使用 sums = nums[i]+nums[j]+nums[left]+nums[right] 会造成溢出
2.8.2 代码实现
1.C++ 代码实现
class Solution {
public:
vector<vector<int>> fourSum(vector<int>& nums, int target) {
vector<vector<int>> result;
sort(nums.begin(), nums.end());
for (int i = 0; i < nums.size(); i++) {
// 这种剪枝是错误的,这道题目target 是任意值
// if (nums[k] > target) {
// return result;
// }
// 去重
if (i > 0 && nums[i] == nums[i - 1]) {
continue;
}
for (int j = i + 1; j < nums.size(); j++) {
// j 是从 i 开始的不是从 0 开始的
if (j > i + 1 && nums[j] == nums[j - 1]) {
continue;
}
int left = j + 1;
int right = nums.size() - 1;
while (right > left) {
// nums[k] + nums[i] + nums[left] + nums[right] > target 会溢出
if (nums[i] + nums[j] > target - (nums[left] + nums[right])) {
right--;
// nums[k] + nums[i] + nums[left] + nums[right] < target 会溢出
} else if (nums[i] + nums[j] < target - (nums[left] + nums[right])) {
left++;
} else {
result.push_back(vector<int>{nums[i], nums[j], nums[left], nums[right]});
// 去重逻辑应该放在找到一个四元组之后
while (right > left && nums[right] == nums[right - 1]) right--;
while (right > left && nums[left] == nums[left + 1]) left++;
// 找到答案时,双指针同时收缩
right--;
left++;
}
}
}
}
return result;
}
};
class Solution:
def fourSum(self, nums: List[int], target: int) -> List[List[int]]:
nums = sorted(nums)
n = len(nums)
res = []
for i in range(n):
if i>0 and nums[i]==nums[i-1]:
continue
for j in range(i+1,n):
if j>i+1 and nums[j]==nums[j-1]: # 防止 j 有重复的情况
continue
left = j+1
right = n-1
while left<right:
if nums[i]+nums[j]+nums[left]+nums[right]>target:
right-=1
elif nums[i]+nums[j]+nums[left]+nums[right]<target:
left+=1
else:
res.append([nums[i],nums[j],nums[left],nums[right]])
# 避免 left 和 right 有重复值的情况下,接着寻找下一组解
while left<right and nums[left]==nums[left+1]:left+=1
while left<right and nums[right]==nums[right-1]:right-=1
left+=1
right-=1
return res
2.8.3时空复杂度
时间复杂度:O(N^3) ; 暴力法:O(N^4)
空间复杂度:O(N)
N数之和总结
N 数之和会给一个数组或者多个数组,求 n 个数相加和为 target 的所有情况。
何时使用哈希表,何时使用双指针:
(1)多个数组,可以重复用 Hash
(2)一个数组,数组内的元素不可重复用双指针
2.快慢指针
2.1 快慢指针原理
当一个跑得快的人和一个跑的慢的人在一个环形的赛道上赛跑,最后跑的快的人会赶上跑的慢的人
所以快指针一次走两步,慢指针一次走一步,最终会相遇在环的某个位置
这个方法用来判断一个链表中是否出现环
2.2 LeetCode 相关习题
142 环形链表 2
解题思路
主要判断:
1.链表是否有环
①存在环:
如果 fast 指针和 slow 指针相遇了,则代表存在环
他们相遇的地方肯定是在环内的某个位置
相遇时 fast 比 slow 多走了 n 圈
②不存在环
fast 最后走向了 None
2.如果有环,环的入口 在哪
①现在假设存在环:
x = 从 head 节点到环的入环口的 step 数
y = 入环口到 fast 和 low 相遇的地方的 step 数
z = 相遇节点剩余部分再到入环口为 z

②相遇时两个节点走的步数
slow : x+y
fast:x+n(y+z)+y
因为快指针是慢指针的两倍,所以走过的步长公式如下:
fast = 2 slow
相关数学公式推导:
等式:2*(x+y)=x+y+n(y+z)
两边消掉一个(x+y): x + y = n (y + z)
因为求的是入口点的举例,所以求得x 的值:x = n (y + z) - y
在从n(y+z)中提出一个 (y+z)来,整理公式之后:x = (n - 1) (y + z) + z
这里的 n 是大于等于1 的,因为 fast 要至少走完 1 圈才会和 slow 相遇
当 n=1 时: x=z
先拿n为1的情况来举例,意味着fast指针在环形里转了一圈之后,就遇到了 slow指针了
当 n>1 时这个等式仍然成立,因为我们所求的是位移,不是路程,所以上面等式和 fast 多绕了几圈是没有关系,不妨碍成立的
③代码设计思路
在存在闭环的情况下,在找到相遇的节点之后,分别定义一个指针从原始出发,然后再定义一个指针从相遇节点出发,走相同的次数后,如果两个指针相遇则相遇的节点就是环的入口
2.2.3 C++ & Python 代码实现
(1)C++ 代码实现
class Solution {
public:
ListNode *detectCycle(ListNode *head) {
// 判空做操作
if(head==NULL||head->next==NULL) return NULL;
ListNode* slow = head;
ListNode* fast = head;
fast = fast->next->next; // 先走两步
slow = slow->next;
while(fast!=NULL&&fast->next!=NULL){
// 判断是否相等:开始放 p,q 指针
if(slow==fast){
ListNode* p = head;
ListNode* q = fast;
// x,z 相遇的地方就是初始节点
while(p!=q){
p = p->next;
q = q->next;
}
return p;
}else{
fast = fast->next->next;
slow = slow->next;
}
}
return NULL;
}
};
1.定义闭环链表(代码直接给出了)
Definition for singly-linked list.
class ListNode:
def __init__(self, x):
self.val = x
self.next = None
2.方法主体
def detectCycle(self, head: ListNode) -> ListNode:
fast,slow = head,head
while fast and fast.next :
fast = fast.next.next # 向前移动一步
slow = slow.next # 向前移动两步
# 如果两个指针指向的值相等,代表存在闭环
if fast == slow: # 这里直接判断的是节点,不是节点里的值
p = head
q =slow
# 当两个值相等的时候就要执行 x=z 的步骤了
while p!=q:
p = p.next
q = q.next
return p # 很奇怪这里返回 q 的结果会是错的
287寻找重复数
2.2.1 算法描述
1.快慢指针法
特殊性:数组中有 n 个位置,能放 1~n+1 的数字,那么根据 “生日原理”,至少有一个数一定是重复的,那么就可以组成一个环。
将 index 和 val 值进行一一对应:
0–>1
1–>3
2–>4
3–>2
4–>2
链表的规则为先从 index = 0 开始,将这一步得到的值看做是下一步的索引值 , next = f(cur) = nums[cur],那么下一步的值就为 1,在下一步的值为 3,nums[3] = 2,所以连成了如下链表

以 [1,3,4,2,2] 数组为例,采用这种方法就会导致 index 重复索引
0 -> 1 -> 3 -> 2 -> 4 -> 2 -> 4 -> …
然后这个题就会转换成上个题,现在就只需要找到环形链表的入口节点即可

2.2.2 C++ 代码实现
class Solution {
public:
int findDuplicate(vector<int>& nums) {
int slow = 0;
int fast = 0;
while(true){ // 这里当做循环链表处理
fast = nums[nums[fast]];
slow = nums[slow];
if(fast==slow){
int p = 0;
int q = slow;
while(p!=q){
p = nums[p];
q = nums[q];
}
return p;
}
}
}
};
2.2.3 时空复杂度
时间复杂度:O(N)
空间复杂度:O(1)
3.滑动窗口
1.基本思想
滑动窗口中用到了左右两个指针,它们移动的思路是:以右指针作为驱动,拖着左指针向前走。右指针每次只移动一步,滑动窗口会变大,右指针走啊走直到滑动窗口的值不满足某个要求了。这时候开始移动左指针,使用 while 循环一直移动直到窗口满足为止。满足后 right 指针可以继续探索新的区域,寻找下一个满足的区间
left 指针的移动是在内部 while 循环中 ; right 指针的移动是当 left 指针满足要求了 right 在 while 循环的最外层移动
窗口内的元素满足某种单调性或特定性质:例如,窗口内的和是递增或递减的。
数组元素均为正数或均为负数:这样窗口的和会随着窗口的扩大而单调变化。
然而,滑动窗口不适用于数组中包含负数的情况,原因如下
2.模板

1.定义两个指针 left ,right ,一起指向起始位置
2.第一重 while 循环让 right 进行移动,相当于对每个字符进行判断
3.第二重循环让 left 移动,将 left 移动到符合题意的那个 index 上
4.right 指针再向前一步探索新的区间
3无重复的最长子串
1. 算法描述
对于例子 abcabcbb 来说,有一个指针 left 需要不断的在字符串上滑动,滑滑滑滑到 abca 时发现产生了重复,
出现重复需要做两件事:
①将最左侧的 a 移走
②left++,也就是将下一个元素作为最长子串的起始位置
用什么判断是否产生了重复:set 判断。
这里需要双指针,一个指针指向非重复字符串的起始位置,一个指针不断的滑动。

2. 代码实现
class Solution {
public:
int lengthOfLongestSubstring(string s) {
int left = 0;
int right = 0;
int res = 0;
unordered_set<char> uset;
while(right<s.size()){
// 判断 set 中是否有重复的元素
while(uset.find(s[right])!=uset.end()){
uset.erase(s[right]);
left++;
}
// 符合条件了,判断符合条件的结果
res = max((right-left+1),res);
uset.insert(s[right]);
right++;
}
return res;
}
};
3. 时空复杂度
时间复杂度:O(N)
空间复杂度:O(∣Σ∣) Σ:字母 ASCII 码的合集
209 长度最小子数组
1. 算法描述
1.求最小子序列可以用滑动窗口解决,滑动窗口中的和为判断数据
2.left ,right 初始化指向 0 index
3.right 向右移动和变大,left 向左移动和变小
4.当滑动窗口中的值大于 target 的时候,left 指针就要逐个向右移动,直到让滑动窗口中的和小于 target
2. C++ 代码实现
class Solution {
public:
int minSubArrayLen(int target, vector<int>& nums) {
int left = 0;
int right = 0;
int sums = 0; // 滑动窗口的大小
int res = INT_MAX; // 最小窗口是无限大
while(right<nums.size()){
sums+=nums[right];
while(sums>=target){ // 当滑动窗口大于 target 的时候就要移动窗口
res = min(res,(right-left+1)); // 判断是否是最小窗口
sums-=nums[left]; // 减掉前面的值
left++; // 移动 left ,一定要先减掉当前值再移动 left
}
// 不满足 sums>target 时,进一步放大窗口
right++;
}
return res == INT_MAX ? 0:res;
}
};
844比较含退格的字符串
3.2.1 算法描述
1.i,j 初始化
i,j 都初始化为 0
2.for 循环判断 j
(1)j == #
i 先判断是否可以推格,然后再推格
(2)j!=#
将 j 赋值给 i 。i,j 同时向前走
3.2.2 C++ 代码实现
class Solution {
public:
void backword(string &str){
// 初始化 i,j
int i =0;
int j =0;
for(int j =0;j<str.size();j++){
if(str[j]=='#'){
if(i>0) i--;
else i=0;
}else{
str[i]=str[j];
i++;
}
}
// 对 str 进行 resize 的操作
str.resize(i);
}
bool backspaceCompare(string s, string t) {
// 处理 s
backword(s);
backword(t);
return s==t;
}
};
3.2.3 时空复杂度
时间复杂度:O(m+n)
空间复杂度:O(1)
3.2.4 知识扩展
1.如何对字符串进行 resize
这里删除完字符后还要对字符串进行 resize 操作。最后的 i 是停留在了当前操作的字符上,所以直接对 i 进行 resize
str.resize(i);
80删除有序数组中的重复项 II
3.3.1 算法描述
这里实现在保留 k=2 个字符的情况下进行删除。
举例:
[1,1,1,1,1,1,2,2,2,2,2,2,3]
首先先对前两个 1 进行保留,所以将 i,j 初始化为 2
这个 j 是否进行保留其实是判断的 i = 0 的这种情况。如果 nums[2] != nums[0] 则这个 nums[j] 是可以保留的也就是赋值给 nums[i] 。假设说 j = 8,那么它需要判断的 index 就是 index = 6 ,而不是 index =7
总结:
因为可以保留 k 个元素,所以前 k 个元素无论是什么都可以保留,所以 i 和 j 从 k 开始便利。
j 一直往前走,我们不用管和 j 相邻的那个 i 是多少,我们只要关注 j 的前 k 个那个 i 是否和 j 相同。
如果不相同那这个 j 是可以赋值给 i 的,相同了则继续判断
3.3.2 C++ 代码实现
class Solution {
public:
int del(vector<int>&nums,int k){
int i =k;
int j =k;
for(;j<nums.size();j++){
if(nums[i-k]!=nums[j]) nums[i++] = nums[j];
}
return i;
}
int removeDuplicates(vector<int>& nums) {
if(nums.size()<2) return nums.size();
int len = del(nums,2);
return len;
}
};
3.3.3 时空复杂度
时间复杂度:O(n)
空间复杂度:O(1)
27 移除元素(easy)
算法描述
这个题是比较典型的快慢指针,一个赋值指针 i 一个赋值指针 j ,j 是不断向前移动的,只有当 j 满足某个条件后将 nums[j] 的值赋给 nums[i] i 才会移动
代码实现
class Solution {
public:
int removeElement(vector<int>& nums, int val) {
int i = 0; // 赋值指针
int j = 0; // 移动指针
while(j<nums.size()){
if(nums[j]==val) j++;
else nums[i++] = nums[j++];
}
return i;
}
};
时空复杂度
时间复杂度:O(N)
空间复杂度:O(1)
2799 统计完全子数组的数目
2. CPP 代码实现
class Solution {
public:
int countCompleteSubarrays(vector<int>& nums) {
set<int> my_set(nums.begin(),nums.end());
map<int,int> my_map;
int diff = my_set.size();
my_set.clear();
int i = 0;
int j = 0;
int res = 0;
while(j<nums.size()){
my_map[nums[j]]++;
while(my_map.size()==diff){
res+=nums.size()-j;
// 将 i 往前提一个,一直提到不满足 diff
my_map[nums[i]]--;
if(my_map[nums[i]]==0) my_map.erase(my_map.find(nums[i]));
i++;
}
j++;
}
return res;
}
};
4.二分法
二分法查找的数组一定是有序的,或者区域有序。对于二分法有几个问题需要思考
1.开区间还是闭区间
2. while 循环的退出条件
3. left right 指针在什么时候移动
4. while 退出后 left 和 right 指向元素有什么含义
2.1_704二分查找
2.1.1 算法思路
二分查找思路:
在 left+right 正常情况下 mid 是会偏左,所以如果想让 mid 偏右必须要进行 +1
模板1:
二分查找 mid 选取哪个值比较关键。如果说
int mid = (left+right)/2;
那么分成的区间就是 [l,mid] & [mid+1,r]。如果满足条件了就让 r 或者 l 移动到对方最后或者起始的位置。因为每次都要 check mid 值是否满足,所以假如说 mid 在 r 的范围内,且 mid 满足条件,就说明 l 不满足条件。那么就需要移动 l 的位置了。否则移动 l 的位置
所以模板如下:
int bsearch_1(int l, int r)
{
while (l < r)
{
int mid = (l + r)/2;
if (check(mid)) r = mid;
else l = mid + 1;
}
return l;
}
模板2:
当想让 mid 在右边时就要进行 +1 操作
int mid = ( l + r + 1 ) /2;
上面的方法分成的区间就在 [l,mid-1]&[mid,r]
int bsearch_2(int l, int r)
{
while (l < r)
{
int mid = ( l + r + 1 ) /2;
if (check(mid)) l = mid;
else r = mid - 1;
}
return l;
}
2.1.2 代码实现
1.左闭右闭
class Solution {
public:
int search(vector<int>& nums, int target) {
int l = 0;
int r = nums.size();
while(l<r){
int mid = (l+r)/2;
if(nums[mid]==target) return mid;
else if(nums[mid]>target) r = mid; // mid 应该在左边
else l = mid+1;
}
return -1;
}
};
2.1.3 时空复杂度
时间复杂度:O(logn)
空间复杂度:O(1)
33搜索旋转排序数组
二分法
3.4.1算法描述
本题反转后的数组可以被拆分成两个有序的子序列。被切分后就转换成了两个有序子序列,所以想到了二分法,left 在 0 right 指向 n-1:
int mid = (right+left)/2;
在这里求出 mid 后有一点是确定的:
[left,mid] 和 [mid.right] 之间肯定有一个子数组是有序的,并且 target 一定是在一个有序数组中找到的(子数组个数等于1 也是有序子数组)
那我们就可以用排除法先定位到,target 是否在其中一个有序数组里!
- (1) 判断是否有序:
左侧有序:nums[left]<=nums[mid]
右侧有序:nums[right]>=nums[mid]
- (2) target 是否在这个有序数组里(这里假设左边有序)
// target 不在这个有序数组中
target<nums[left] || target>nums[mid]
// target 在有序数组中
else if(target>nums[left] && target<nums[mid]) right = mid-1;
else return left;
- (3)移动 left right 位置,缩小答案范围
最后 left right 进行了更新,计算出新一轮 mid ,再循环上面找有序数组的步骤
2. C++ 代码实现
class Solution {
public:
int search(vector<int>& nums, int target) {
int n = nums.size();
int left = 0;
int right = n-1;
while(left<right){
int mid = (right+left)/2;
if(nums[mid]==target) return mid;
// 找到有序数组
if(nums[left]<=nums[mid]){
if(target<nums[left] || target>nums[mid]) left = mid+1;
else if(target>nums[left] && target<nums[mid]) right = mid-1;
else return left;
} else if(nums[right]>=nums[mid]){
if(target>nums[right] || target<nums[mid]) right = mid-1;
else if(target>nums[mid] && target<nums[right]) left = mid+1;
else return right;
}
}
return nums[left]==target?left:-1;
}
};
3.4.3 时空复杂度
时间复杂度:O(logn) 二分查找
空间复杂度:O(1)
3.8_34在排序数组中查找元素的第一个和最后一个位置
3.8.1 算法描述
这个题可以化为找到第一个 target 出现的位置和最后一个 target 出现的位置
(1)二分法设置
区间:左闭右闭
循环条件:left <= right
退出条件:left > right
如果 nums[mid] <= target 移动的是 left 的话,那么最后 left 停在的位置一定是不满足该条件的,反而 nums[right] 可满足该条件
如何移动:
当 nums[mid] > target 和 nums[mid] < target 时正常移动 left 和 right 指针
a.nums[mid] = = target 但是还想继续往左找:right = mid-1
b.nums[mid] = = traget 但还想继续往右找 left = mid+1
(1)这里我们先找最后一个 target 出现的位置
如果持续遇到 nums[mid] = = target 就要持续向右找,left = mid+1
退出条件就是 left > right 即 nums[left] = nums[right+1],最后停留的 nums[left] 一定不满足 nums[left]<=target ,所以最后答案在 nums[right] 上
(2)其次找 traget第一次出现的位置
如果持续遇到 nums[mid] = = target 就要持续向左找,right = mid-1
退出条件就是 left > right 即 nums[left] = nums[right+1],最后停留的 nums[right] 一定不满足 nums[left]>=target ,所以最后答案在 nums[left] 上
3.8.2 代码实现
class Solution {
public:
vector<int> searchRange(vector<int>& nums, int target) {
int n = nums.size();
if(n==0) return {-1,-1};
// 先找到第一个位置
int left = 0;
int right = n-1;
// 退出条件: left>right
// left = right+1
// left 退出的点为 nums[left] > target
// 所以 nums[right] <= target
while(left<=right){
int mid = (left+right)/2;
if(nums[mid]<=target) left = mid+1;
else right = mid-1;
}
if((right==n || right<0)||nums[right]!=target) return vector<int>{-1,-1};
int right_res = right;
left = 0;
// 退出条件 left > right
// left = right+1
// nums[right] 最后指向 target 前一个
while(left<=right){
int mid = (right+left)/2;
if(nums[mid]>=target) right = mid-1;
else left = mid+1;
}
if((left<0||left==n)||nums[left]!=target) return vector<int>{-1,-1};
return vector<int>{left,right_res};
}
};
3.5_69 Sqrt(x)
二分法
3.5.1 算法描述
这道题是求平方,正常思路是从 mid 开始找找 [1,mid] 所有数看那个数符合结果,这属于一种暴露解。
还有一种方法是使用二分,二分相比于暴力解可以更快的找到答案
这个题的二分法比较特殊,不像查找中的二分法必须要找到才能返回,这里是无论放如何都能找到,所以在 <=x 的时候多出来一个变量 res 用于一直记录结果
因为最终结果需要转换成 int ,所以在 mid*mid <x 的时候对 mid 进行取值
举例:

3.5.2 C++ 代码实现
1.二分法
public:
int mySqrt(int x) {
int left = 0;
int right = x;
int res = 0;
while(left<=right){
int mid = left+(right-left)/2;
long ji = (long)mid*mid;
if(ji<=x){
res = mid;
left = mid+1;
}else{
right = mid-1;
}
}
return res;
}
};
3.5.3 时空复杂度
时间复杂度:O(logN)
空间复杂度:O(1)
275 H指数2
1.算法描述
方法1:
方法2:
假设有 n 篇论文,那么对于索引 i 位置的论文:
它的引用次数是 citations[i]。i 后面一共有 n - i 篇论文(包括 i ),这些论文都被引用了至少 citations[i] 次
所以我们只要找到一个最小的 i,使得:
citations[i] >= n - i
这时候说明有 n - i 篇论文引用次数 ≥ n - i,所以 h = n - i 是可能的 H 指数。
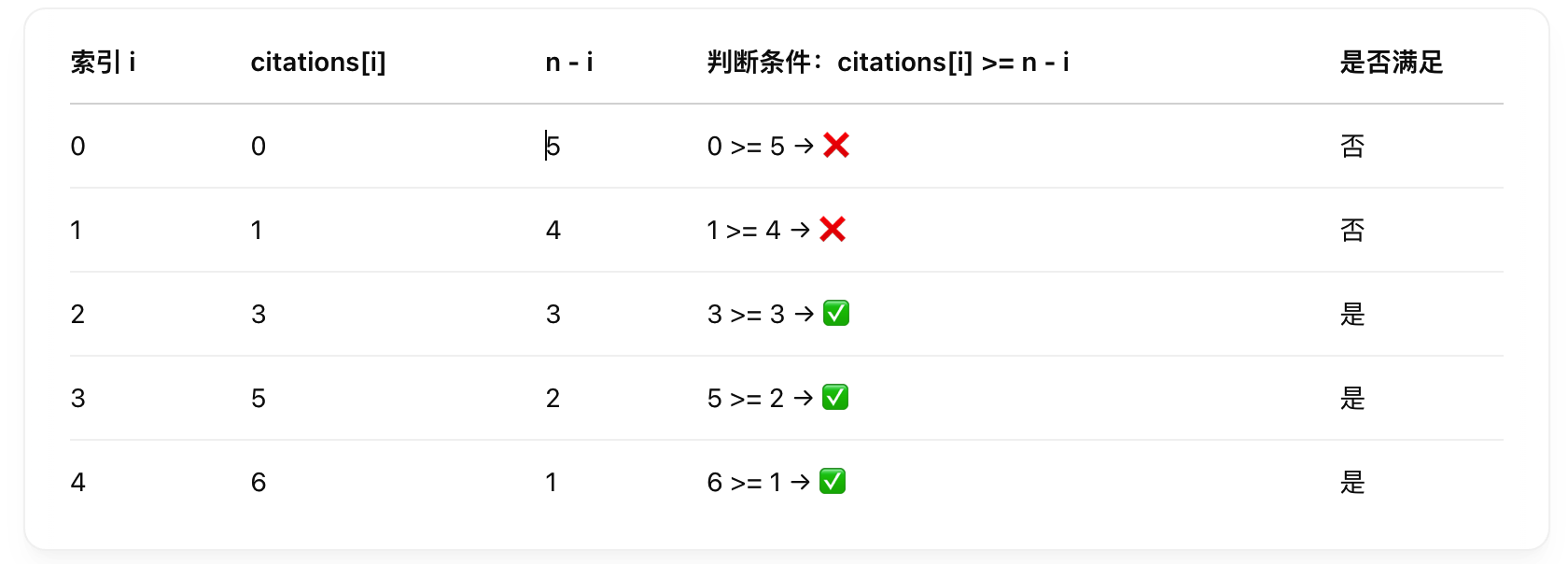
假设引用次数数组为:
citations = [0, 1, 3, 5, 6]
我们可以通过二分查找来找这个最小的 i。target 就是上面的代码公式
我们从头到尾看看每个索引 i:
2.Cpp代码
class Solution {
public:
int hIndex(vector<int>& citations) {
int n = citations.size();
int left = 0;
int right = n-1;
while(left<=right){
int mid = (left+right)/2;
if(citations[mid]>n-mid) right = mid-1;
else if (citations[mid]==n-mid) return n-mid;
else left = mid+1;
}
return n-left;
}
};





 本文通过解析LeetCode中的经典问题,如移除元素、反转字符串、两数之和、判断回文等,详细介绍了快慢指针算法的应用。探讨了如何利用快慢指针在链表、数组和字符串操作中寻找重复、环路和最长子串。
本文通过解析LeetCode中的经典问题,如移除元素、反转字符串、两数之和、判断回文等,详细介绍了快慢指针算法的应用。探讨了如何利用快慢指针在链表、数组和字符串操作中寻找重复、环路和最长子串。
















 859
859

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








