该笔记为自动驾驶之心课程总结
Pure Pursuit
下面是对于一个纯跟踪算法来说,给定一个目标点,如何计算需要控制的方向盘转角。
S1:找到目标点(look-ahead point)
找到我们需要跟踪的目标点后可以连接目标点和自车当前位置生成一个弦,再基于该弦可以得到一个圆,车辆可以根据该圆得到前轮转角 δ
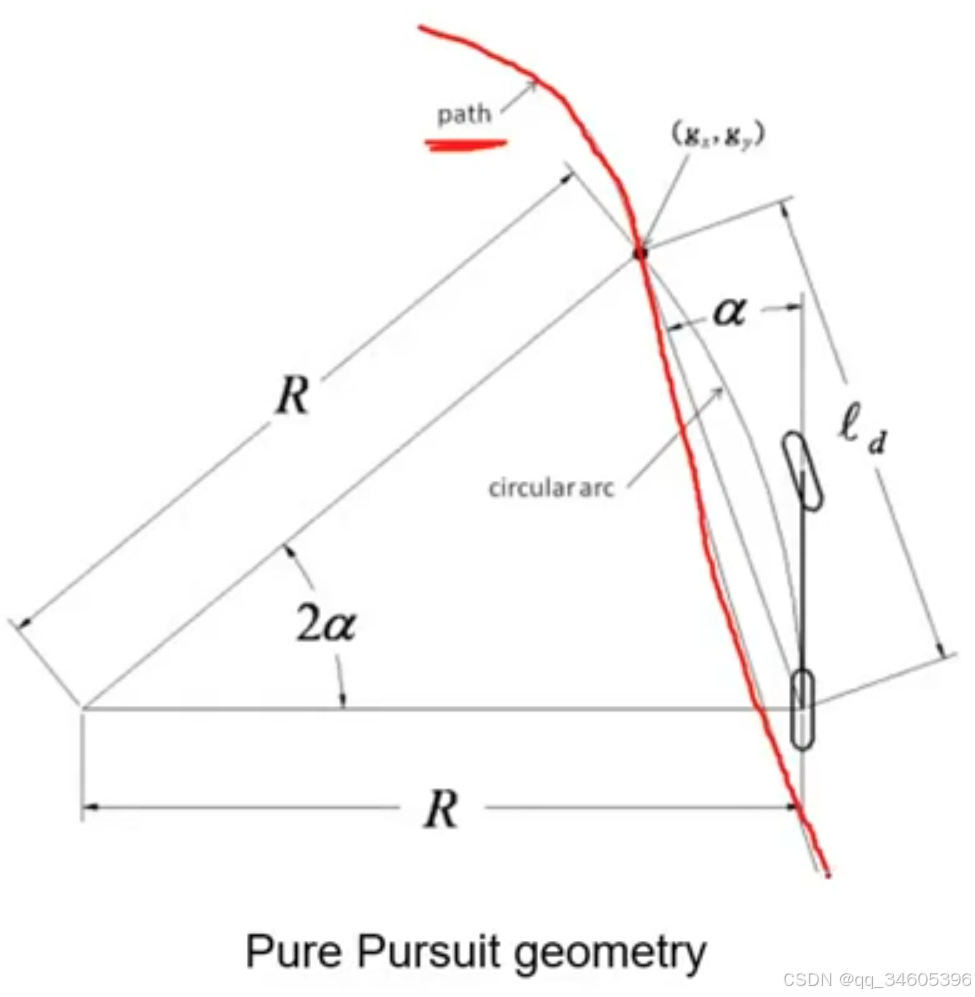
S2:得到该圆弧的曲率
ld 代表弦长,α 代表自车与目标之间方向角上的差距,根据下面的曲三角关系可以得到曲率
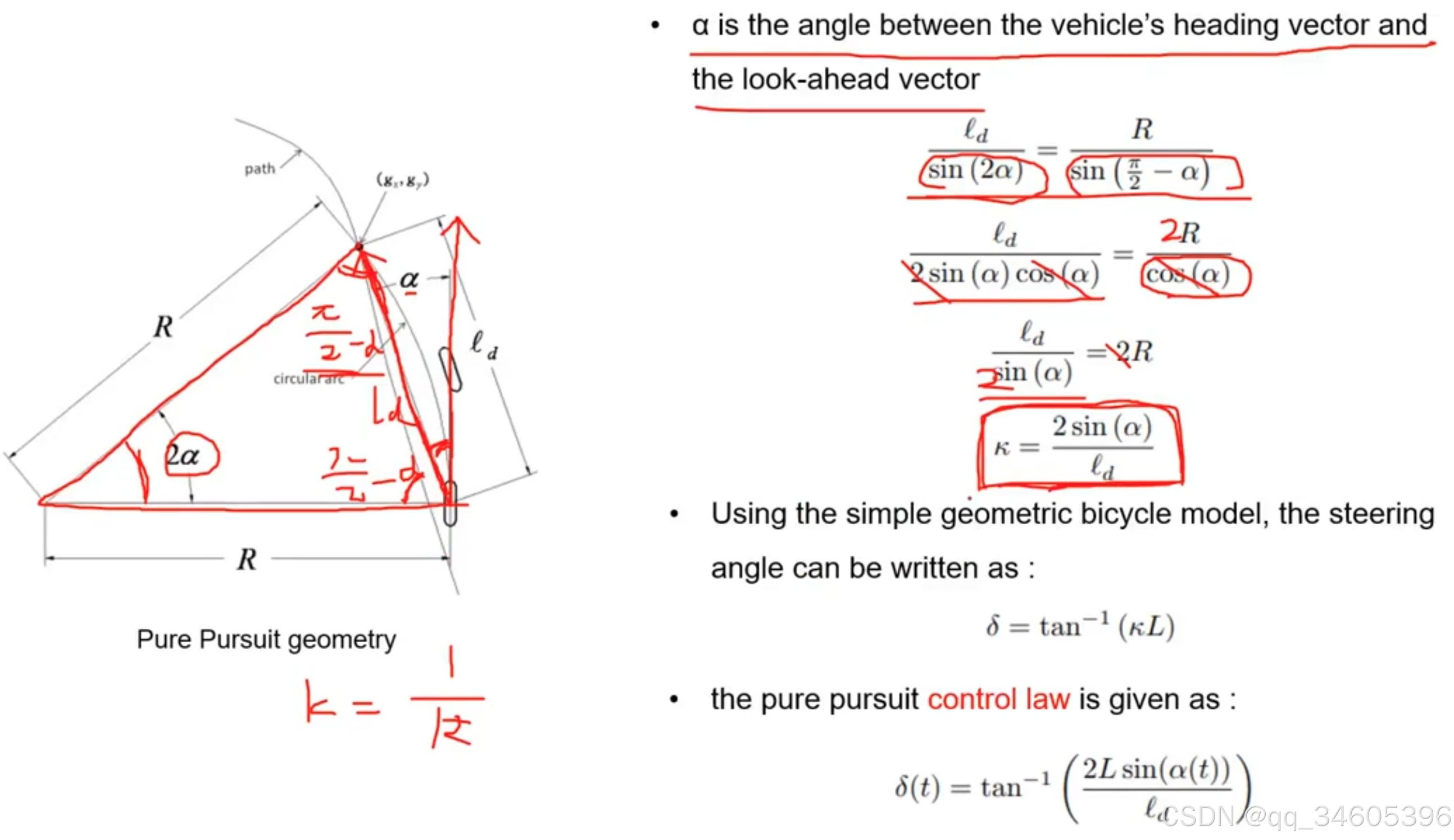
S3:根据圆弧曲率求出目标转角
知道曲率就可以求出方向盘转角

将 α 转换为 e_ld 进行计算:
这里的 e_ld 为当前位置和目标点横向相差的距离,这里通过相关计算将 α 转换为 e_ld
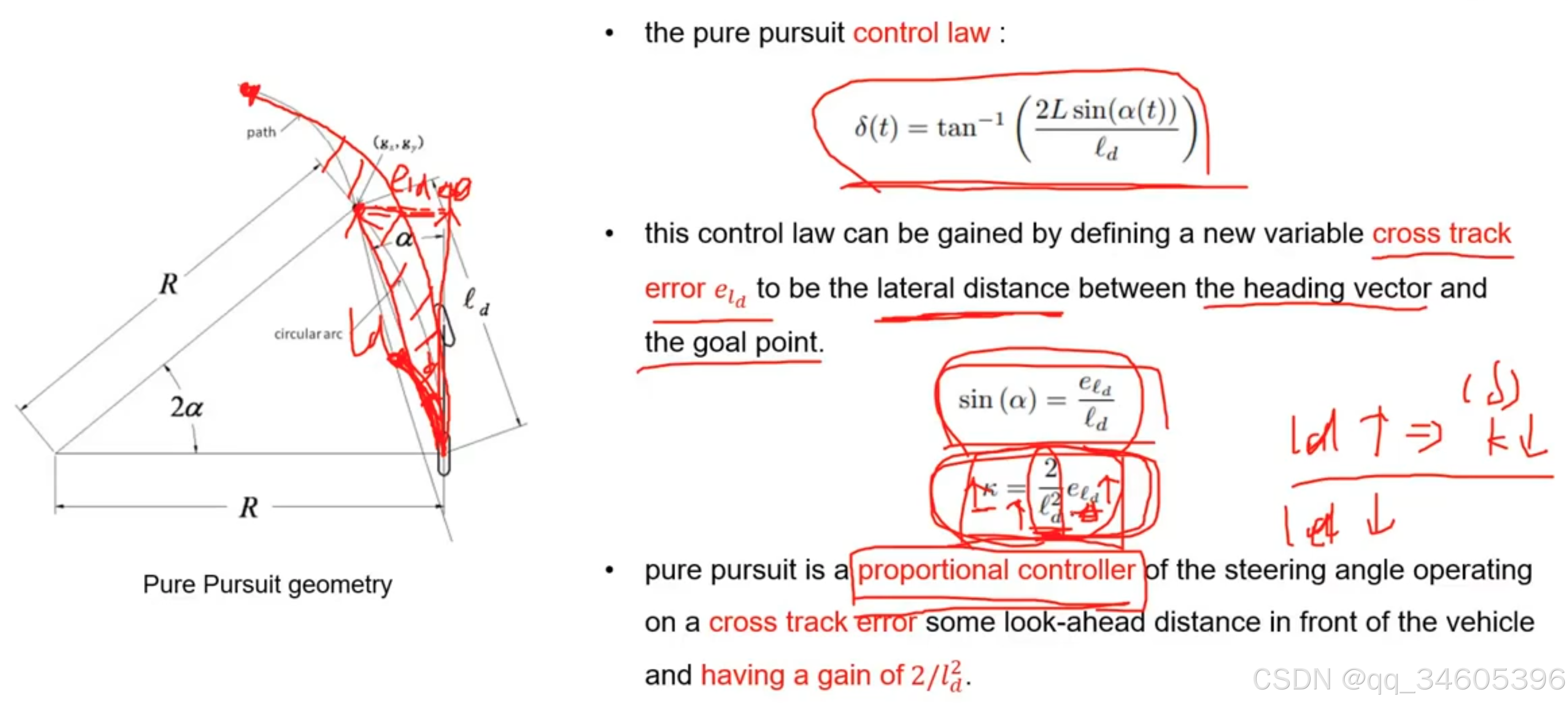
将 δ 转换为一个和速度相关的量:
δ(t)=tan−1(2Lsin(α)kvx(t))\delta(t) = \tan^{-1} \left(\frac{2L \sin(\alpha)}{k v_x(t)}\right)δ(t)=tan−1(kvx(t)2Lsin(α))
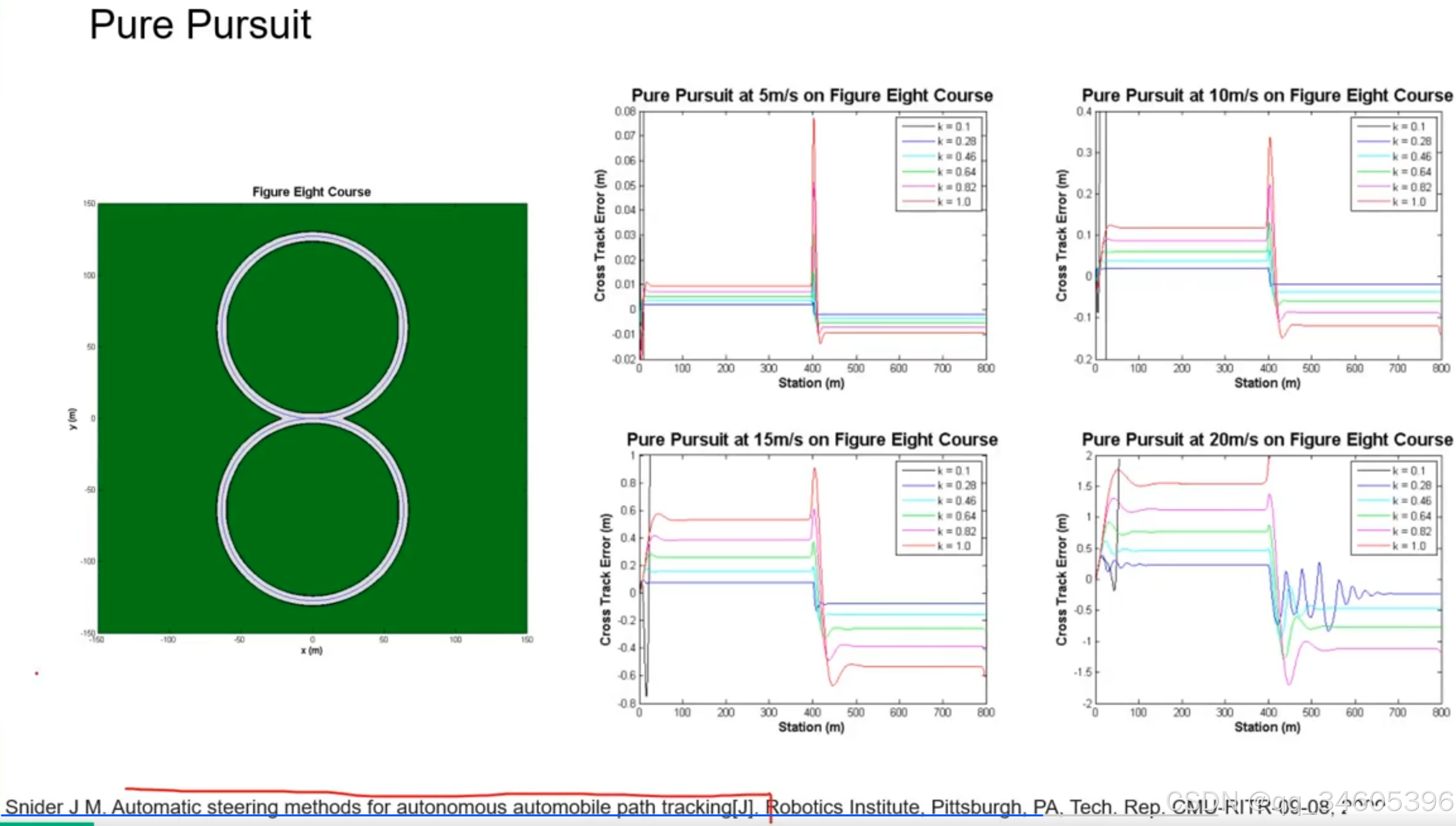
下图中以 20m/s 的速度观察,当系数 k 比较大时误差在刚开始也比较大,当 k 比较小时虽然一开始误差小但是震荡也比较大
PID
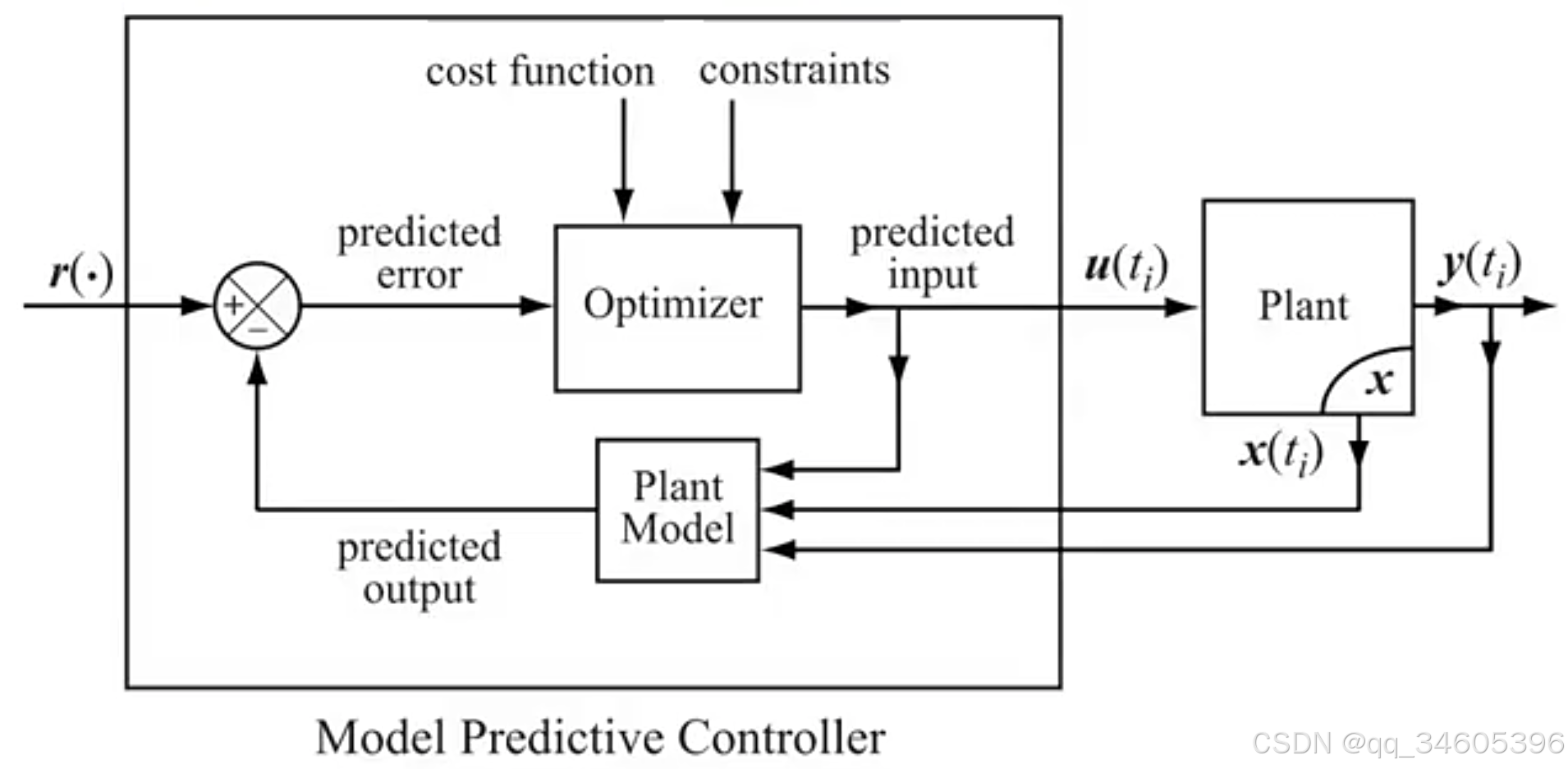
PID:Proportional(比例)、Integral(积分)、Differential(微分)。在下图当中,r(t) 代表目标的坐标及状态,u(t) 代表通过系统计算出来的控制信号,e(t) 是目标点 r(t) 和实际状态 y(t) 之间的差值,即 e(t) = r(t)-y(t),整个系统就是对 e(t) 进行调整最终输出更可靠的控制指令
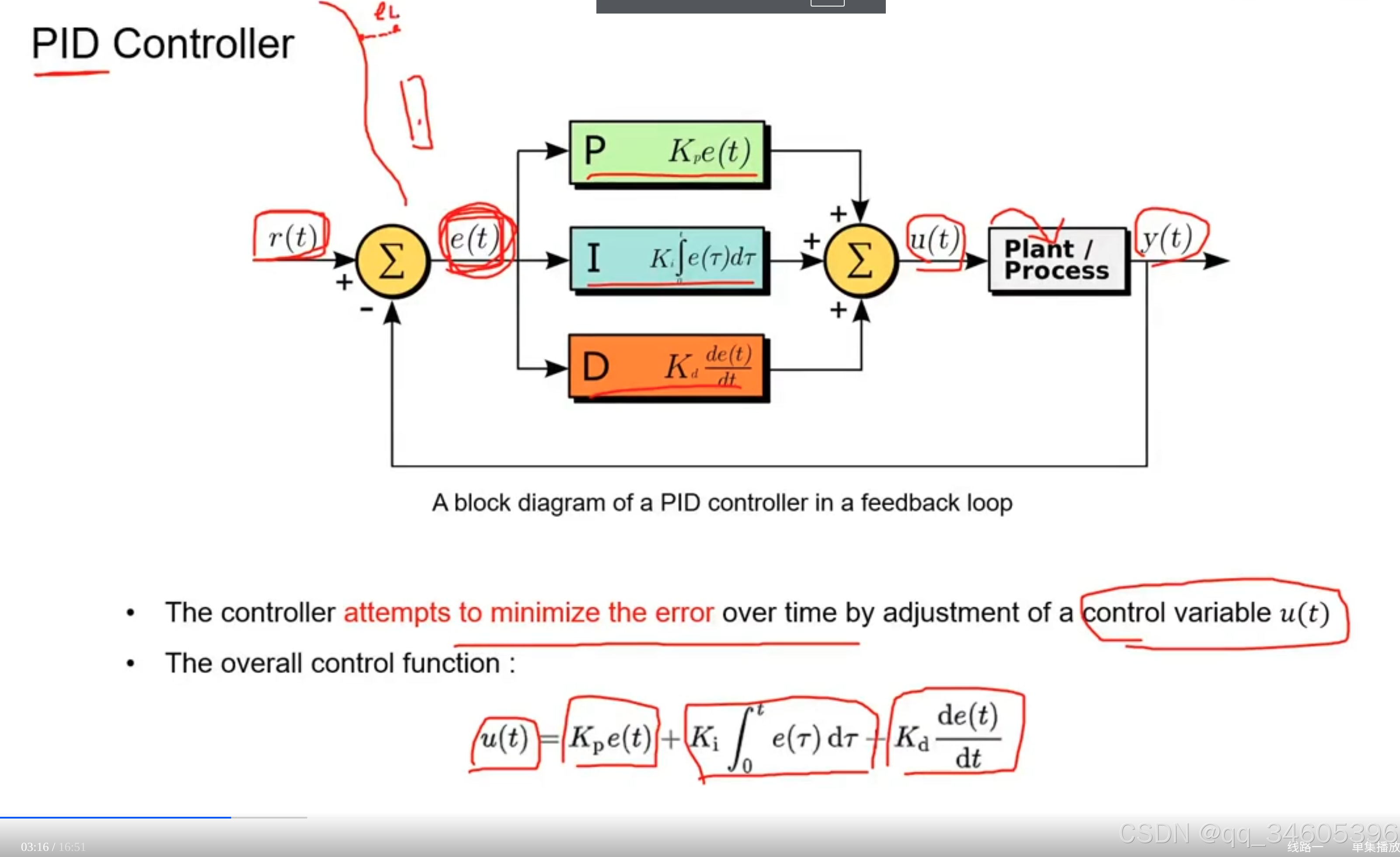
PID 尝试减小 error 最终调整 u(t)
积分:将一定时间内的误差进行累计再积分。系统一旦出现了偏差,比例调节立即产生调节作用用以减少偏差
微分:对整个误差的变化率进行记录,可以以现在状态预测未来状态。因此能产生超前的控制作用,在偏差还没有形成之前,已被微分调节作用消除
下图为不同的 K 值对输出结果的影响:
(1)P 项

K 值越大虽然能越早接近于参考值,但是震荡也会比较大
(2)积分项

有时候误差比较小时很难用误差项去弥补,但是如果误差累计比较大就容易用积分解决误差。同理如果系数设置的过大会导致超调并且震荡
(3)微分项

比如当前变化率是一个负值,代表 error 不断在减小,那么 PID 整体就是不断减小
LQR
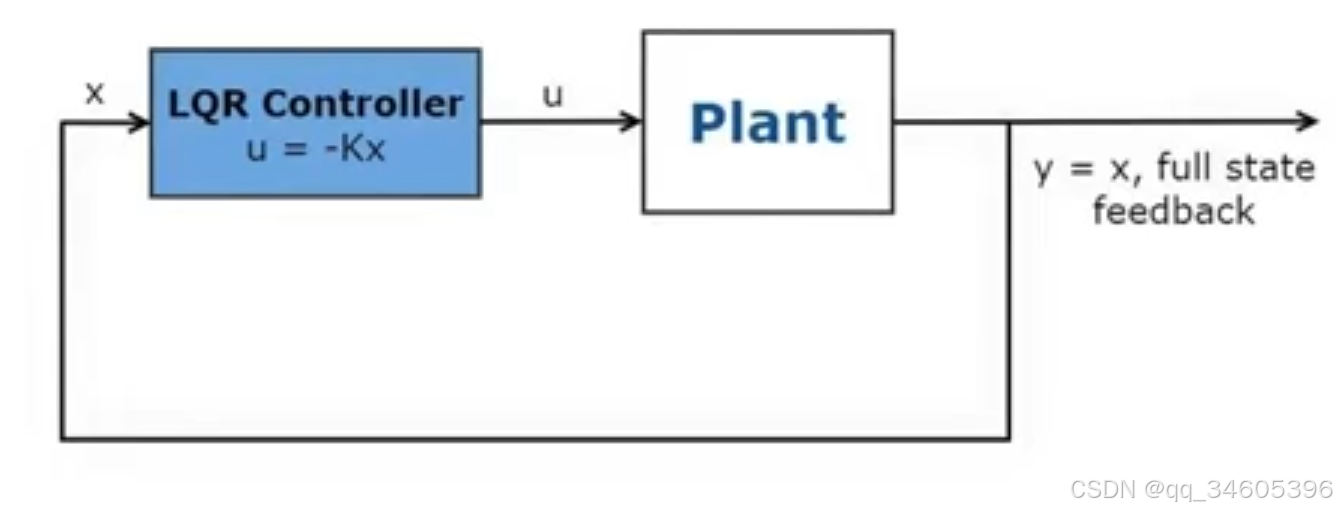
LQR (Linear Quadratic Regulator)线性二次反馈器。是一个线性状态反馈控制器,他的状态转移方程可以线性化表示出,目标是最小化二次型的代价函数,这里的反馈是指需要求出反馈矩阵 K 给到控制量 u。
LQR 标准的二次方程:
J=∫0∞(xTQx+uTRu) dtx˙=Ax+Bu\begin{align*}
J &= \int_{0}^{\infty} (x^T Q x + u^T R u) \, dt \\
\dot{x} &= A x + B u
\end{align*}Jx˙=∫0∞(xTQx+uTRu)dt=Ax+Bu
其中 QR 是 x 和 u 的权重
控制率:
LQR 的最终目标就是求出 K,当输入 x 时得到最终的控制 u ,下面就是如何求出 K
u=−K⋅xK=R−1BTPATP+PA+Q−PBR−1BTP=0\begin{align}
u &= -K \cdot x \\
K &= R^{-1} B^T P \\
A^T P + P A + Q - P B R^{-1} B^T P &= 0
\end{align}uKATP+PA+Q−PBR−1BTP=−K⋅x=R−1BTP=0
LQR 的整体步骤就是:先定义 QRAB 四个矩阵,然后计算出黎卡提 Riccati 中的矩阵 P ,通过 P 就可求出 K。在这里 x 可以传入的状态有很多,比如当前位置状态,或者当前 error 的值,都可以拟合 LQR 控制器
LQR 状态转移方程线性转换
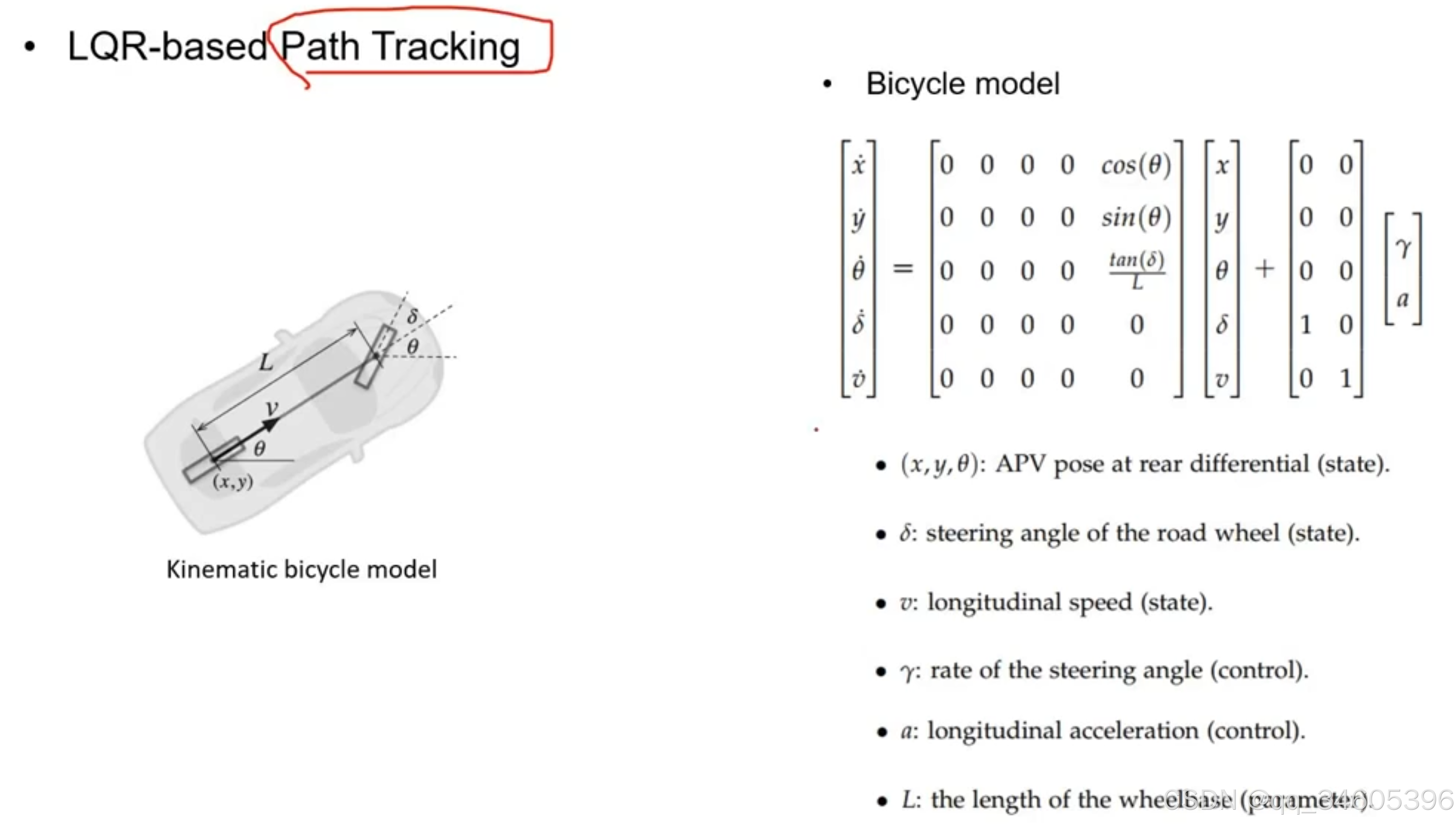
自行车模型公式如下,已知下面的状态量:
这里的 u 为后面的方向盘转速和 a ,x 为(x,y,Θ…) 等这些状态量。一个线性的公式表达如下:x‘ = Ax+Bu,但是下面的公式很明显,x 前面的 A 中包含很多 cos sin 的计算,这些计算都是非线性的
如下图所示,以后轴中心为中心,红色的点为跟踪参考点 (x*,y*)。d 为参考点方向的法线距离,也就是自车与参考点的距离
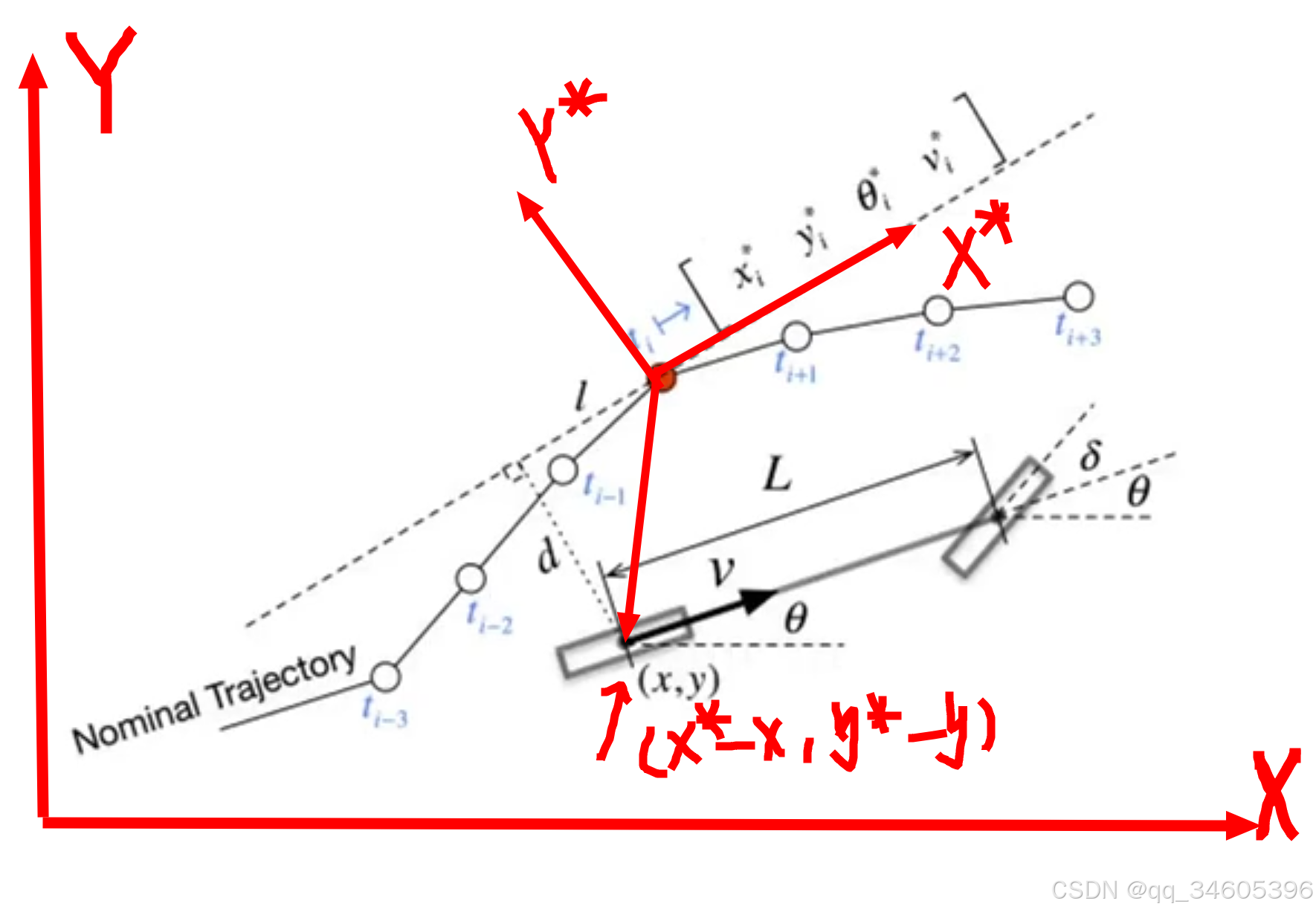
新 x 的表达式为
x=[x1x2x3]=[dθ∗−θδ]x=\left[\begin{array}{l}
x_{1} \\
x_{2} \\
x_{3}
\end{array}\right]=\left[\begin{array}{c}
d \\
\theta^{*}-\theta \\
\delta
\end{array}\right]x=x1x2x3=dθ∗−θδ
因为现在要求 d 的大小,所以将 (x,y) 映射到 (x*,y*) 上
d 的值为:
d=sinθ∗⋅x−cosθ∗⋅y+(x∗+cosθ∗)⋅x∗−(y∗+sinθ∗)⋅x∗=sinθ∗⋅(x−x∗)−cosθ∗⋅(y−y∗)\begin{align*}
d &= \sin\theta^* \cdot x - \cos\theta^* \cdot y + (x^* + \cos\theta^*) \cdot x^* - (y^* + \sin\theta^*) \cdot x^* \\
&= \sin\theta^* \cdot (x - x^*) - \cos\theta^* \cdot (y - y^*)
\end{align*}d=sinθ∗⋅x−cosθ∗⋅y+(x∗+cosθ∗)⋅x∗−(y∗+sinθ∗)⋅x∗=sinθ∗⋅(x−x∗)−cosθ∗⋅(y−y∗)
状态转移方程中,要想求出 A,B 矩阵的值就要先对 x 求导:
在求导时 x* 之类的都看作一个常数,根据上面车辆动力学公式 x’ = cos(Θ)v, y’ = vsin(Θ),再根据车辆动力学推出其他相关的公式并化简得到,x1,x2,x3 的导数:
x˙1=d˙=v⋅sinθ∗⋅cosθ−v⋅cosθ∗⋅sinθ=v⋅sin(θ∗−θ)=v⋅sin(x2)x˙2=−θ˙=−v⋅tanδ=−vL⋅tan(x3)x˙3=δ\begin{align*}
\dot{x}_1 &= \dot{d} = v \cdot \sin\theta^* \cdot \cos\theta - v \cdot \cos\theta^* \cdot \sin\theta \\
&= v \cdot \sin(\theta^* - \theta) = v \cdot \sin(x_2) \\
\dot{x}_2 &= -\dot{\theta} = -v \cdot \tan\delta = -\frac{v}{L} \cdot \tan(x_3) \\
\dot{x}_3 &= \delta
\end{align*}x˙1x˙2x˙3=d˙=v⋅sinθ∗⋅cosθ−v⋅cosθ∗⋅sinθ=v⋅sin(θ∗−θ)=v⋅sin(x2)=−θ˙=−v⋅tanδ=−Lv⋅tan(x3)=δ
整体推导如下图所示:
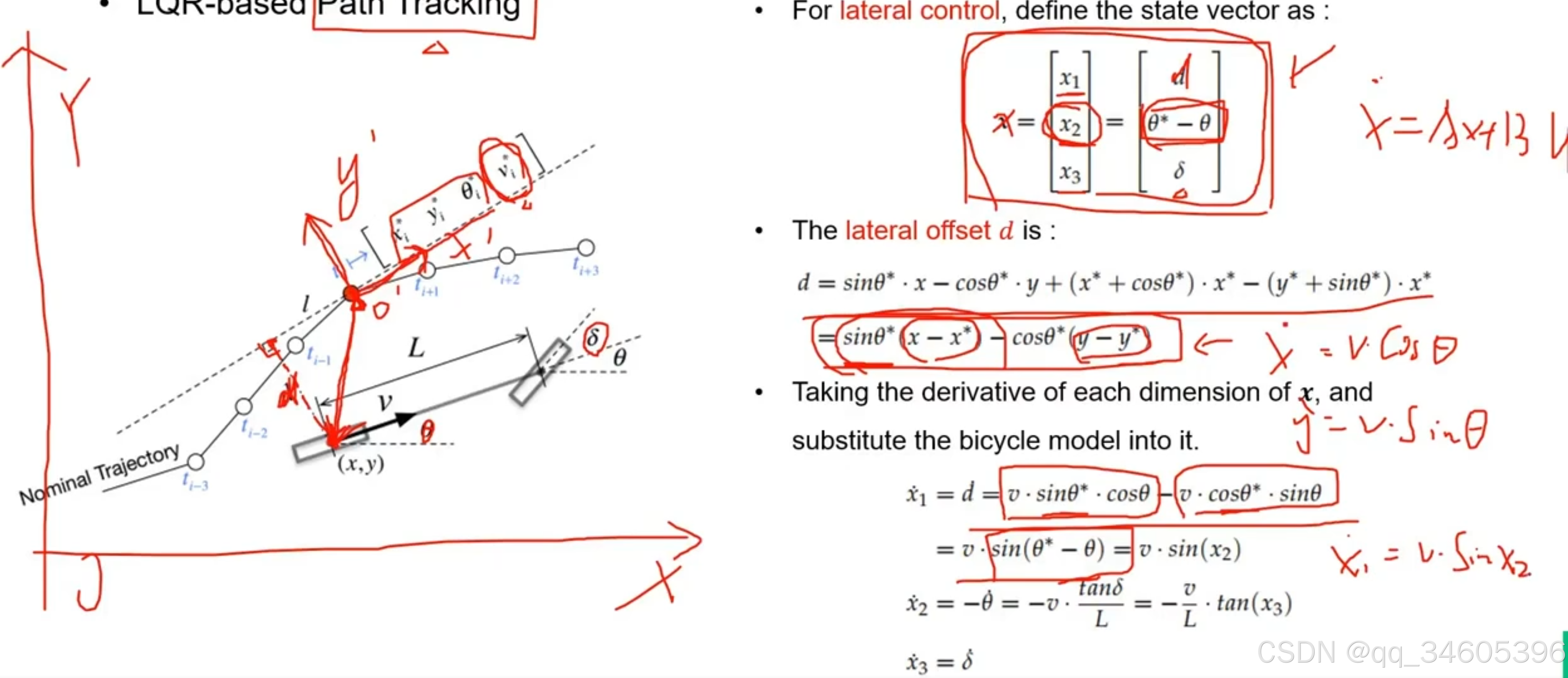
这里假设我们将 Θ*-Θ 的值看做非常小,将 δ 的值也看做非常小就可以得到下面的 A,B 矩阵。这里转换为线性系统的精髓就是将 sin cos 等三角函数的计算约等于一些长度
[x˙1x˙2x˙3]=[0v000−vL000][x1x2x3]+[001]δ˙\left[\begin{array}{c}
\dot{x}_{1} \\
\dot{x}_{2} \\
\dot{x}_{3}
\end{array}\right]=\left[\begin{array}{ccc}
0 & v & 0 \\
0 & 0 & -\frac{v}{L} \\
0 & 0 & 0
\end{array}\right]\left[\begin{array}{l}
x_{1} \\
x_{2} \\
x_{3}
\end{array}\right]+\left[\begin{array}{l}
0 \\
0 \\
1
\end{array}\right] \dot{\delta}x˙1x˙2x˙3=000v000−Lv0x1x2x3+001δ˙
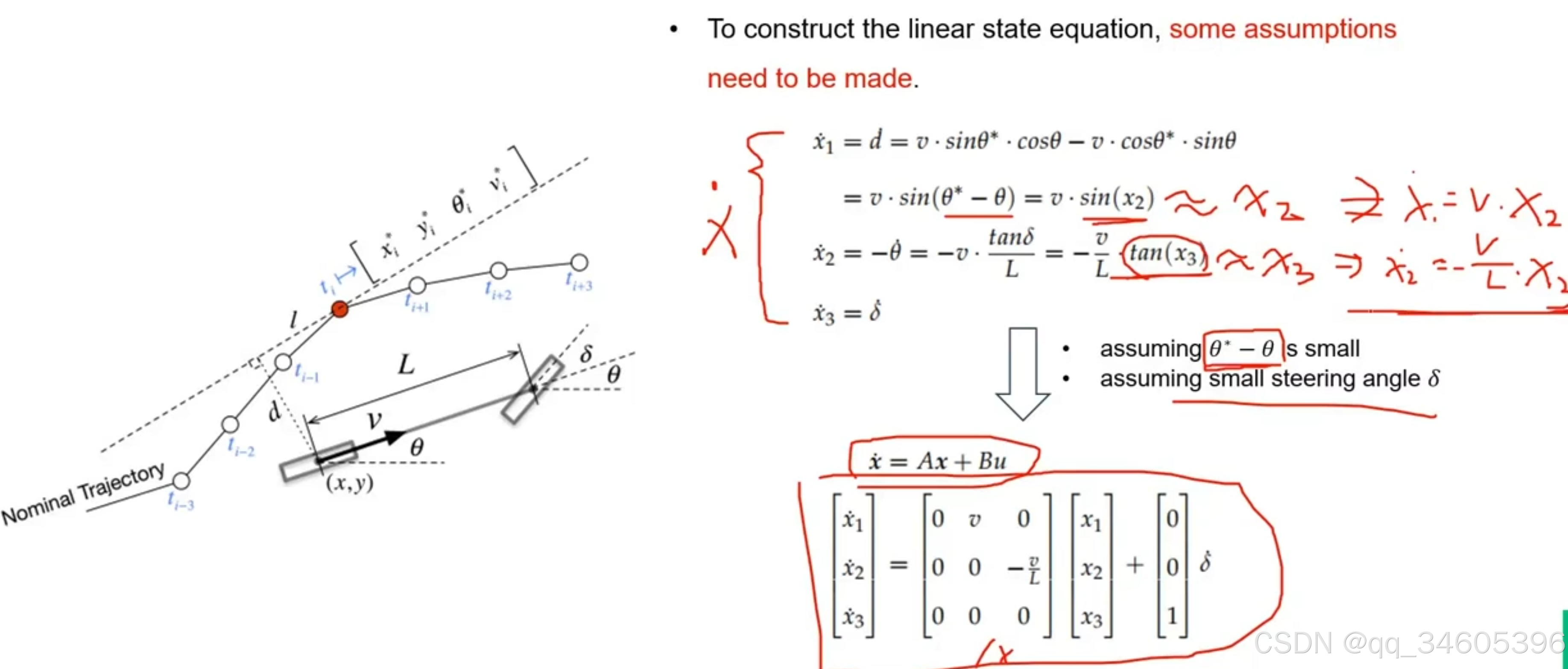
LQR 纵向跟踪任务推导
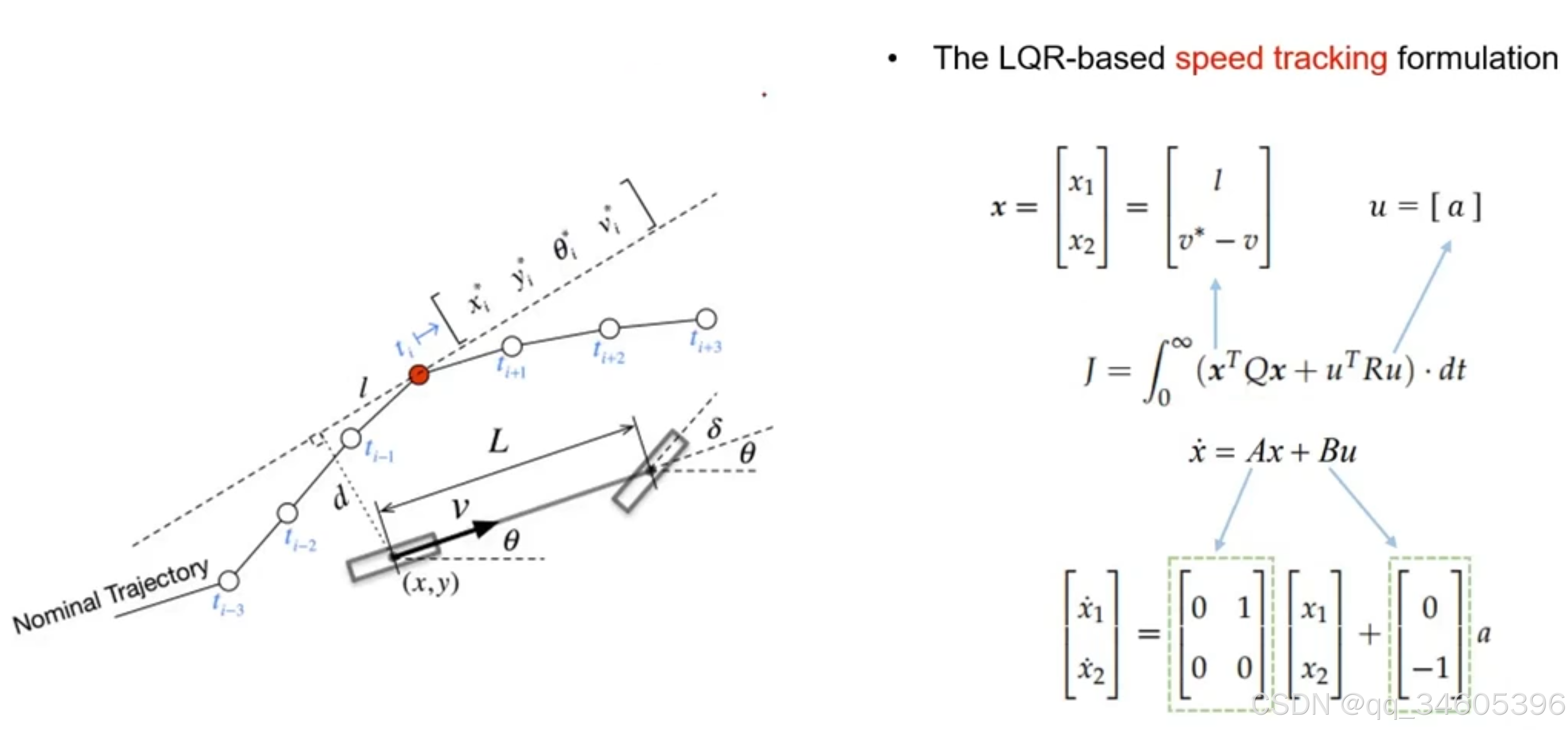
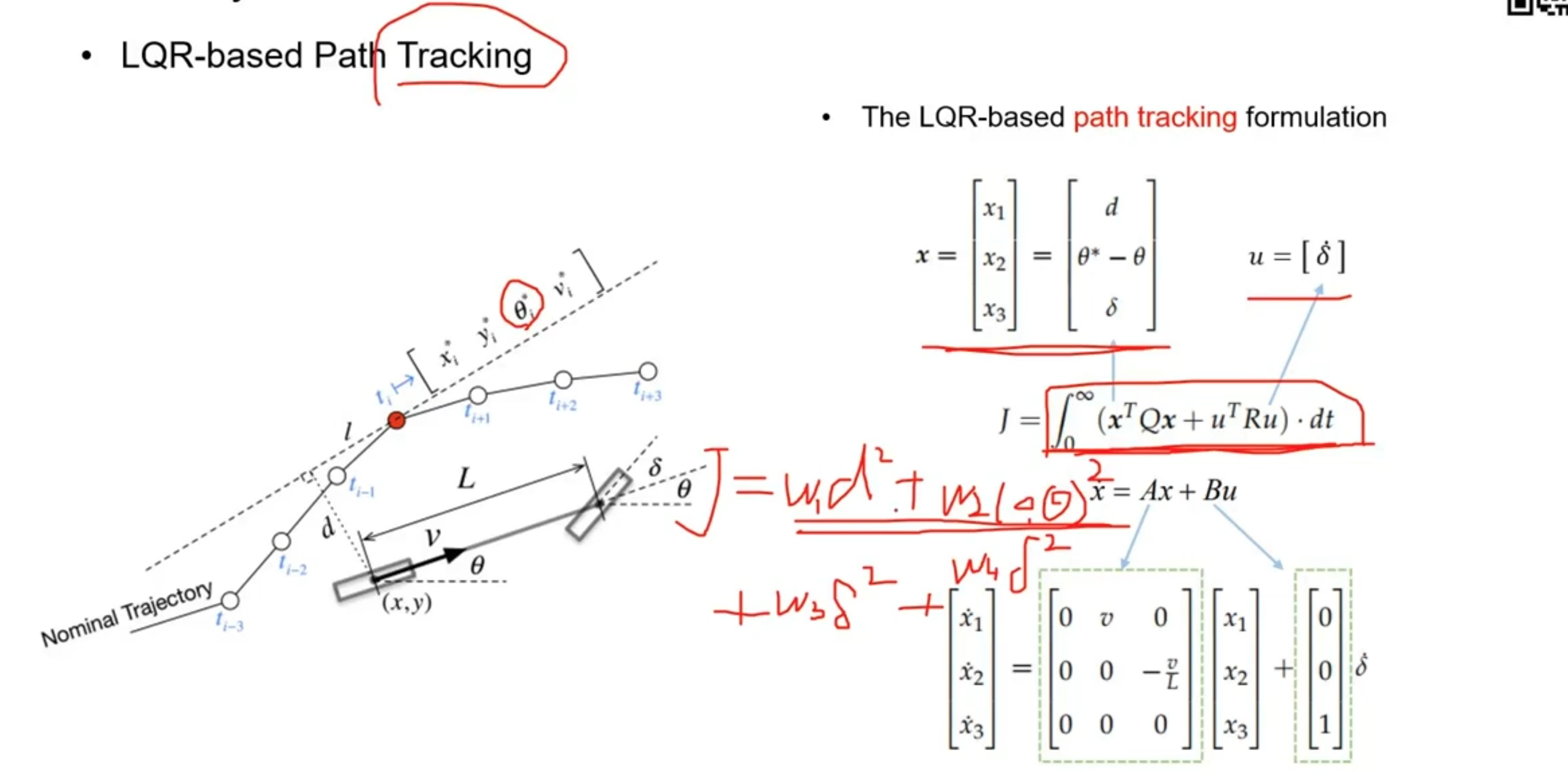
LQR 目代价方程的含义
这边已纵向跟踪为例。 将 x 进行平方,u 进行平方就可以转换为公式
J=w1d2+w2(θ)2+w3∗δ2J = w1d^2+w2(\theta)^2+w3*\delta^2 J=w1d2+w2(θ)2+w3∗δ2 那么意义就是:
d:希望自车和目标点的距离接近,Θ 为 heading 角接近,δ\deltaδ就是希望 yaw_rate 尽可能小
MPC
基本概念
MPC(Model predictive control) 基于模型预测的控制器,该方法也是通过计算控制动作用于减少代价函数
Ut∗(x(t)):=argminUt∑k=0N−1q(xt+k,ut+k) subj. to xt=x(t) measurement xt+k+1=Axt+k+But+k system model xt+k∈X state constrain ut+k∈U input constrair Ut={ut,ut+1,…,ut+N−1} optimization vsystemmodelstateconstraintsinputconstraintsoptimizationvariables
\begin{array}{rll}
U_{t}^{*}(x(t)):=\underset{U_{t}}{\operatorname{argmin}} & \sum_{k=0}^{N-1} q\left(x_{t+k}, u_{t+k}\right) & \\
\text { subj. to } & x_{t}=x(t) & \text { measurement } \\
& x_{t+k+1}=A x_{t+k}+B u_{t+k} & \text { system model } \\
& x_{t+k} \in \mathcal{X} & \text { state constrain } \\
& u_{t+k} \in \mathcal{U} & \text { input constrair } \\
& U_{t}=\left\{u_{t}, u_{t+1}, \ldots, u_{t+N-1}\right\} & \text { optimization } \mathrm{v}
\end{array}
system model
state constraints
input constraints
optimization variables
Ut∗(x(t)):=Utargmin subj. to ∑k=0N−1q(xt+k,ut+k)xt=x(t)xt+k+1=Axt+k+But+kxt+k∈Xut+k∈UUt={ut,ut+1,…,ut+N−1} measurement system model state constrain input constrair optimization vsystemmodelstateconstraintsinputconstraintsoptimizationvariables
目标函数:
输入是当前状态 x 和控制指令 u ,目标是将 N 个过程的 error 进行累加最终将 error 最小化,在上图中目标函数用 q 表示
预测模型(system model):
该模型就是状态转移方程,可以是基于自行车模型,也可以是别的,它代表下一个时刻的状态与前一时刻状态的关系,可以是线性的可以是非线性的
约束:
约束可以是控制约束,状态约束,线性约束等等
LQR 和 MPC 的对比

相关实例
S1:创建状态模型
状态转移方程如下,x,u 的关系如下图所示
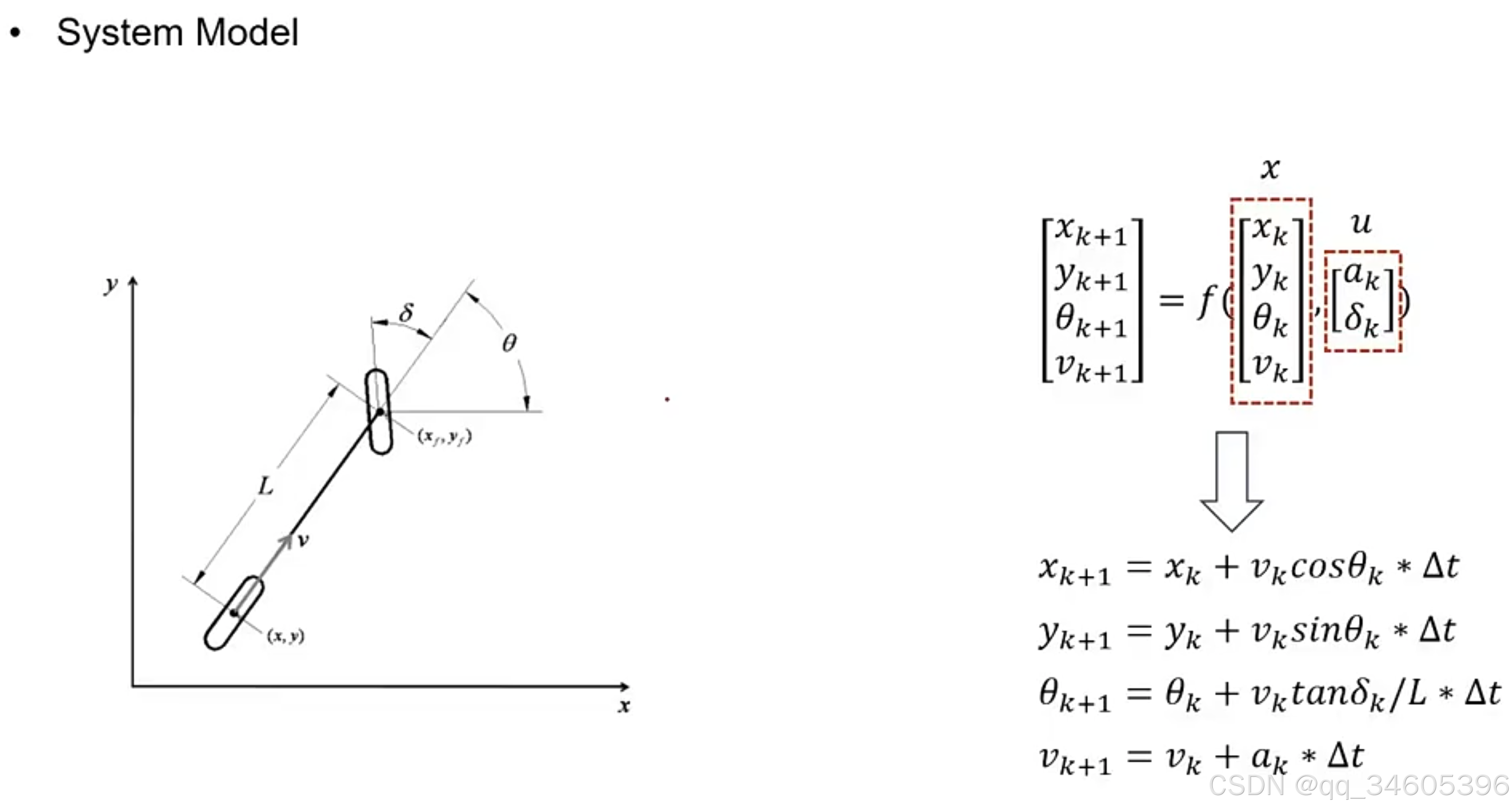
S2:状态方程
下图中红色的线为规划给出的参考轨迹,绿色的线 MPC 优化后生成的轨迹,J 代表代价函数,下面是代价函数的约束
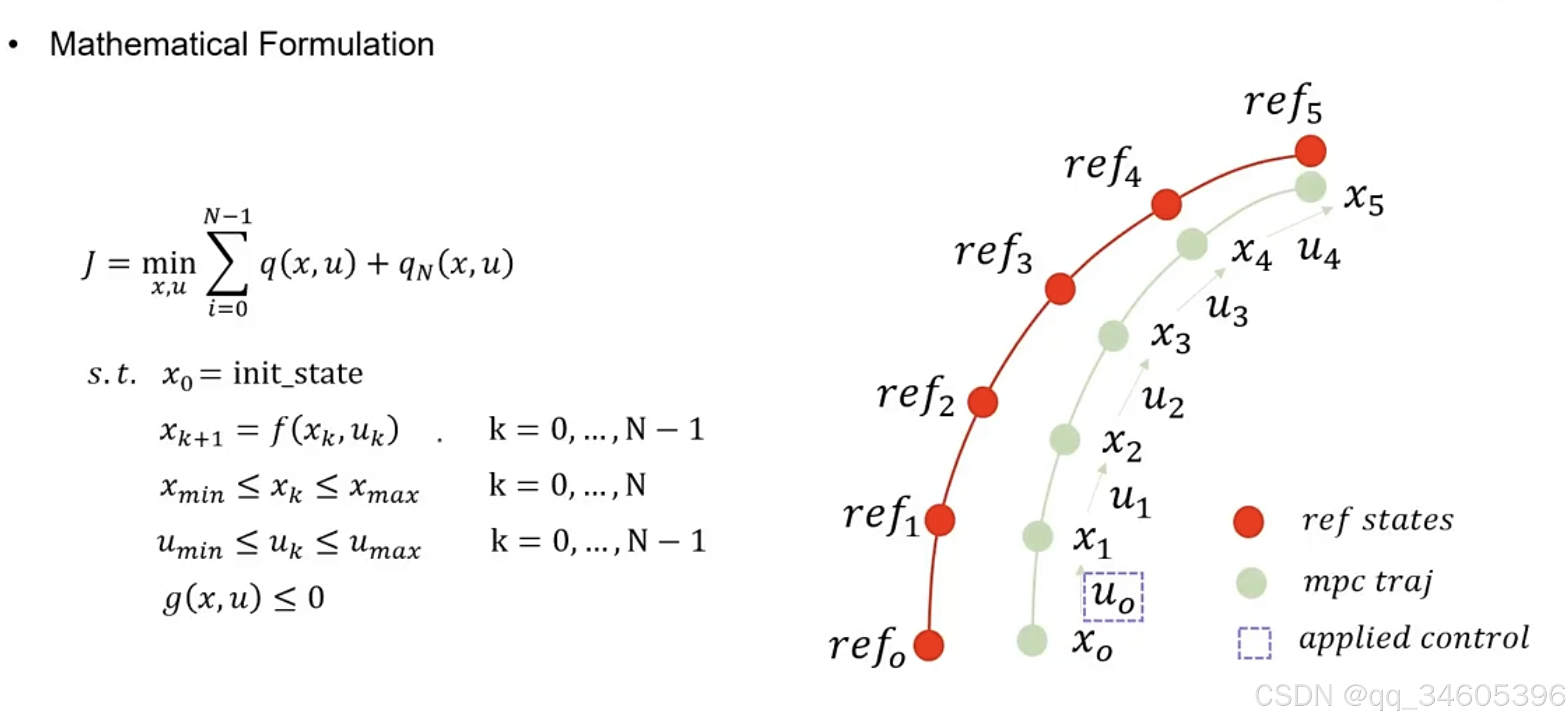
常用的代价函数:
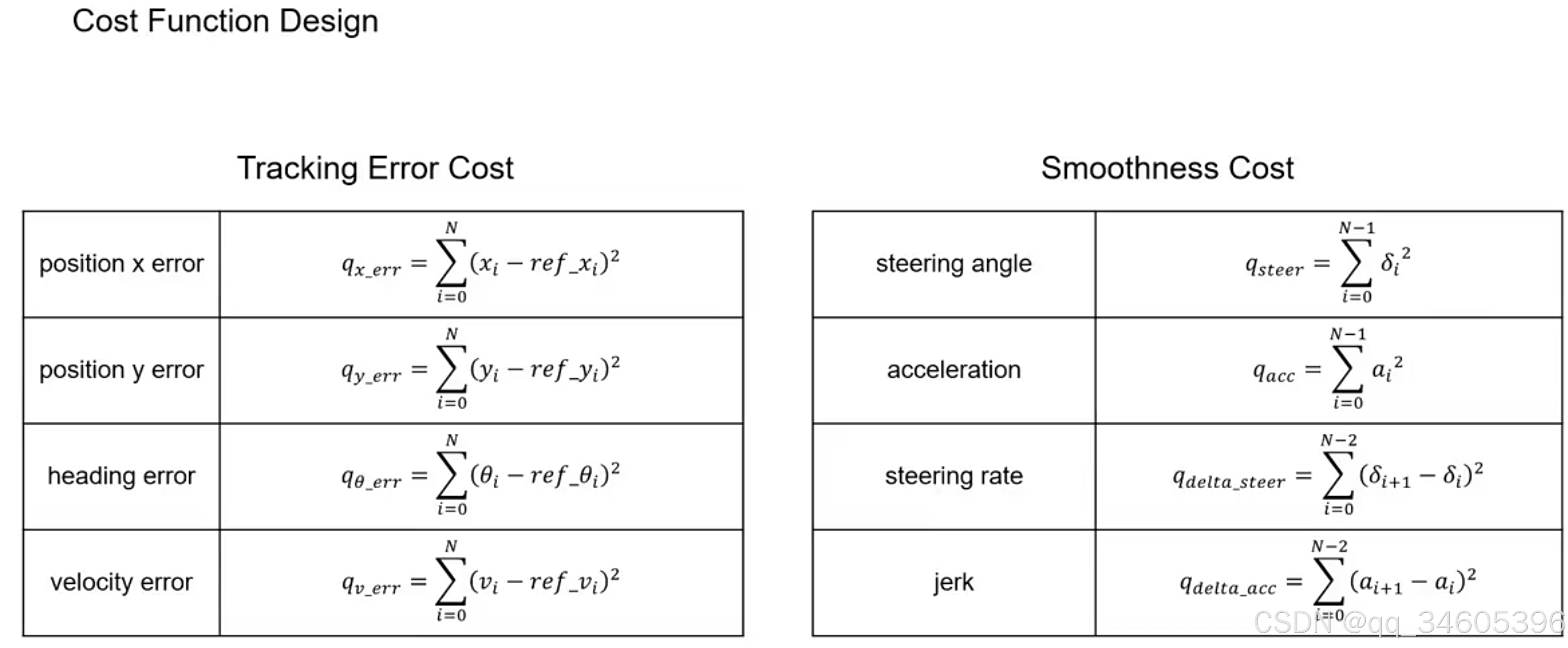
相关约束:

























 1096
1096

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








