*该笔记基于自动驾驶之心课程整理
1.Contingency Planning
假设自车需要左转,在邻车道有个对向 onComing 的车,那么自车有两种方案:
1.加速在近处先拐过去—> 激进决策
2.减速,让对向车过去再拐过去 —> 保守解决
在做这两个决策之前有一段公共距离为红色箭头可以进行选择,这种方法叫做 Tree Planning
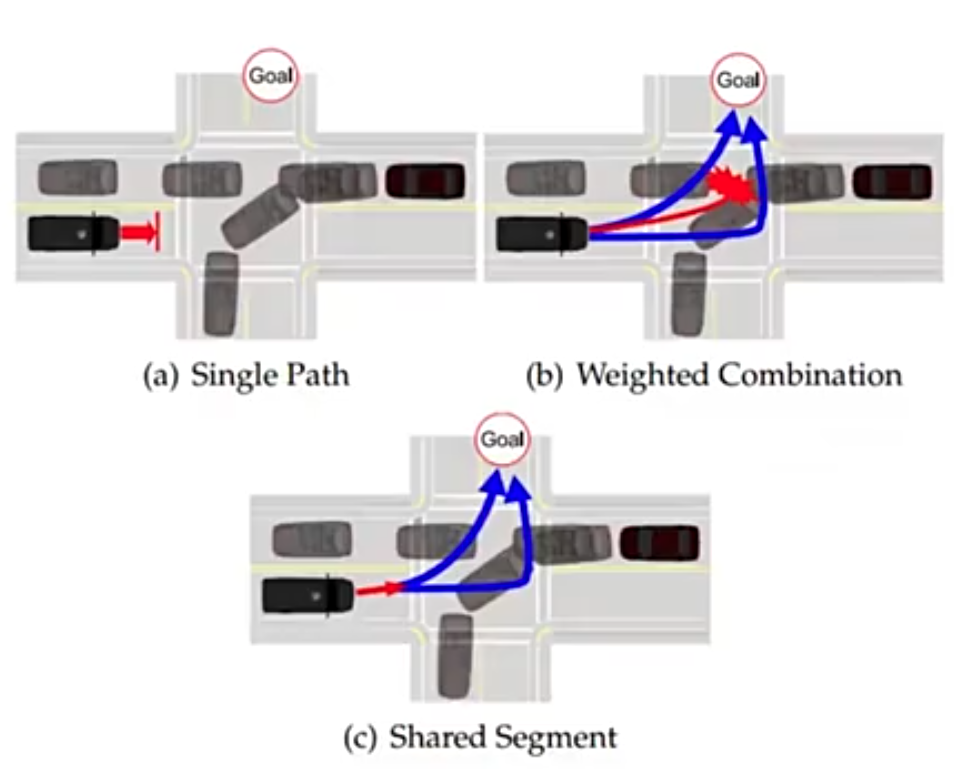
Contingency Planning SL
目标函数:
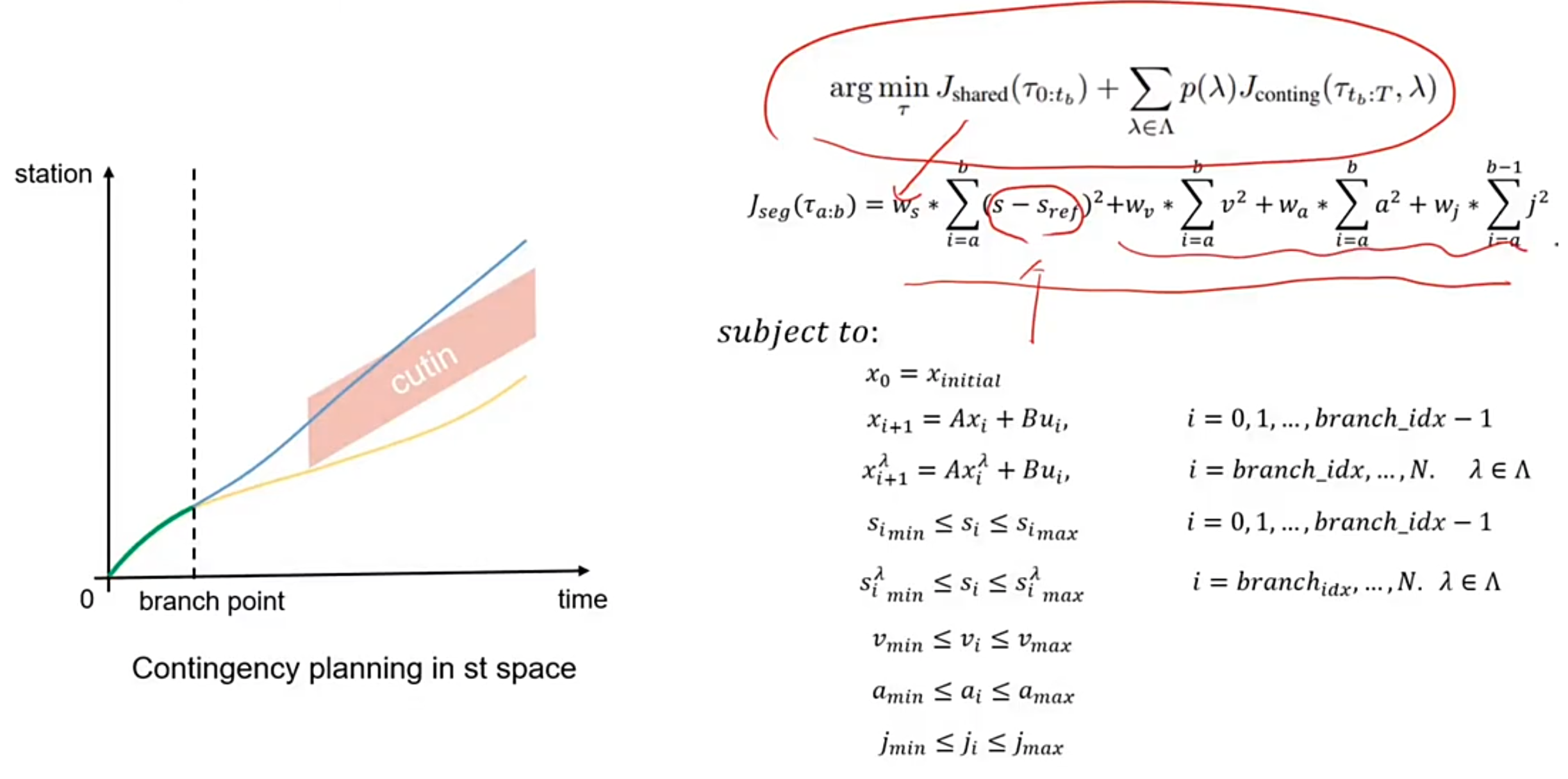
argminτ Jshared(τ0:tb)+∑λ∈Λp(λ)Jconting(τtb:T,λ)s.t. gj(τ)≤bj,j=1,…,n\begin{align*} &\arg\min_{\tau} \; J_{\mathrm{shared}}(\tau_{0:t_b}) + \sum_{\lambda \in \Lambda} p(\lambda) J_{\mathrm{conting}}(\tau_{t_b:T}, \lambda) \\ &\text{s.t. } \quad g_j(\tau) \leq b_j,\quad j = 1, \ldots, n \end{align*}argτminJshared(τ0:tb)+λ∈Λ∑p(λ)Jconting(τtb:T,λ)s.t. gj(τ)≤bj,j=1,…,n
$$J_{\mathrm{seg}}(\tau_{a:b}) = w_{l} \sum_{i=a}^{b} l_{i}^2
- w_{l’} \sum_{i=a}^{b} {l’_{i}}^2
- w_{l’‘} \sum_{i=a}^{b} {l’'_{i}}^2
- w_{l’‘’} \sum_{i=a}^{b-1} {l’‘’_{i}}^2$$
前面代表公共路径中的目标函数,目标函数就是二次型。后面 Jconting(τtb:T)J_{\mathrm{conting}}(\tau_{t_b:T})Jconting(τtb:T) 是每个路径下的目标函数 p(λ)p(\lambda)p(λ) 是每个路径的概率
优化变量
这个和我们的约束差不多
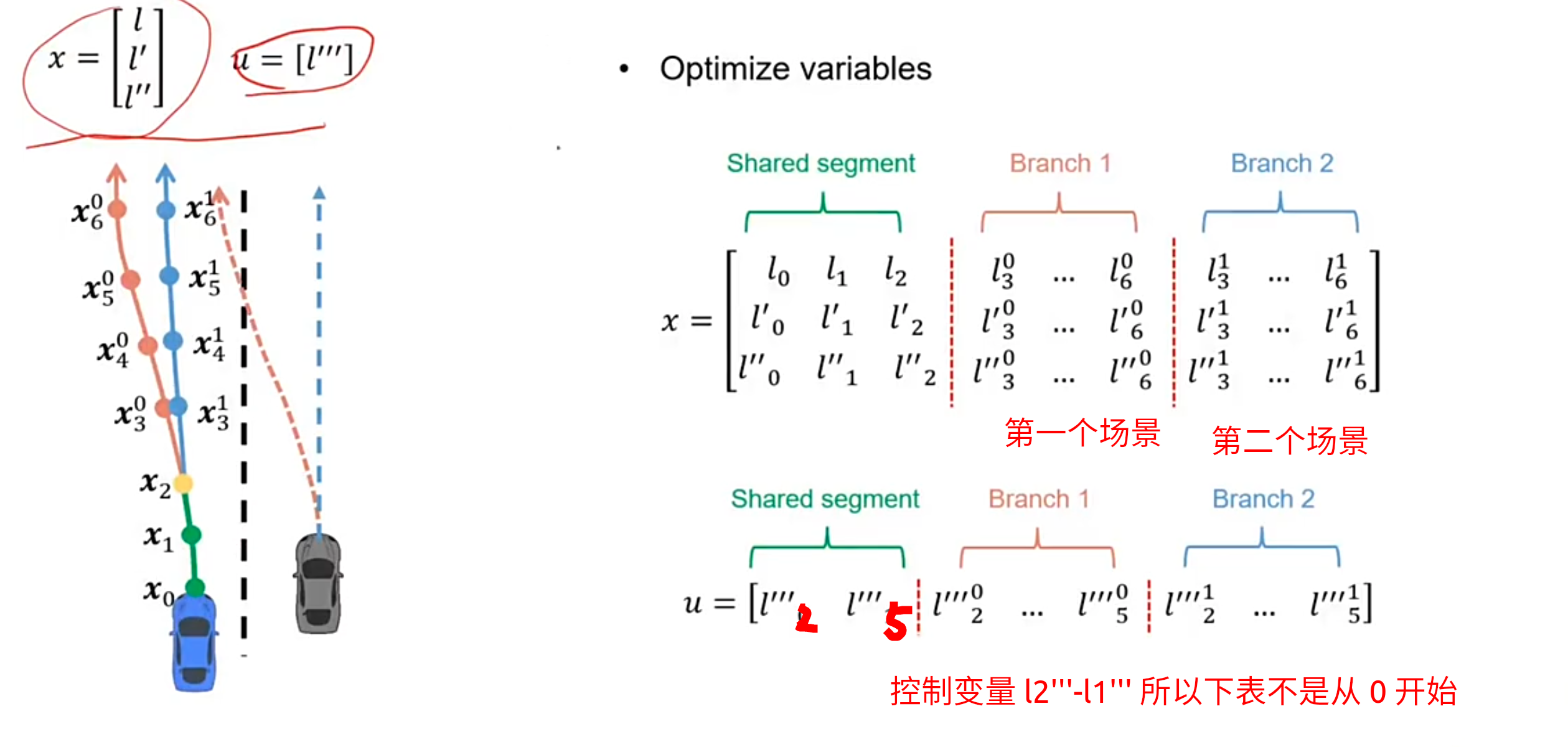
约束
l 相邻点之间的积分约束为:
li+1′′′=li′′+∫0Δsli→i+1′′′ds=li′′+li′′′∗Δsli+1′′=li′+∫0Δsli′′′(s)ds=li′+li′′′∗Δs+12∗li′′′′∗Δs2li+1=li+∫0Δsli′′(s)ds=li+li′′∗Δs+12∗li′′′∗Δs2+16∗li′′′′∗Δs3\begin{aligned}
l_{i+1}''' &= l_{i}'' + \int_{0}^{\Delta s} l_{i \to i+1}''' ds = l_{i}'' + l_{i}''' \ast \Delta s \\
l_{i+1}'' &= l_{i}' + \int_{0}^{\Delta s} l_{i}'''(s) ds = l_{i}' + l_{i}''' \ast \Delta s + \frac{1}{2} \ast l_{i}'''' \ast \Delta s^{2} \\
l_{i+1} &= l_{i} + \int_{0}^{\Delta s} l_{i}''(s) ds \\
&= l_{i} + l_{i}'' \ast \Delta s + \frac{1}{2} \ast l_{i}''' \ast \Delta s^{2} + \frac{1}{6} \ast l_{i}'''' \ast \Delta s^{3}
\end{aligned}li+1′′′li+1′′li+1=li′′+∫0Δsli→i+1′′′ds=li′′+li′′′∗Δs=li′+∫0Δsli′′′(s)ds=li′+li′′′∗Δs+21∗li′′′′∗Δs2=li+∫0Δsli′′(s)ds=li+li′′∗Δs+21∗li′′′∗Δs2+61∗li′′′′∗Δs3
xi+1=Axi+Buix_{i+1} = A x_{i} + B u_{i}xi+1=Axi+Bui
A=[1Δs12Δs201Δs001],B=[16Δs312Δs21]\mathbf{A} = \begin{bmatrix} 1 & \Delta s & \frac{1}{2} \Delta s^{2} \\ 0 & 1 & \Delta s \\ 0 & 0 & 1 \end{bmatrix} ,\quad \mathbf{B} = \begin{bmatrix} \frac{1}{6} \Delta s^{3} \\ \frac{1}{2} \Delta s^{2} \\ 1 \end{bmatrix}A=100Δs1021Δs2Δs1,B=61Δs321Δs21
对于每个 Branch 上的每个点的约束为
xi+1=Axi+Bui,xi+1λ=Axiλ+Bui,i=0,1,…,branch_idx−1i=branch_idx,…,N,λ∈Λ\begin{aligned}
x_{i+1} &= A x_{i} + B u_{i}, \\
x_{i+1}^\lambda &= A x_{i}^\lambda + B u_{i},
\end{aligned}
\quad i=0,1,\dots, \text{branch\_idx}-1
\quad i=\text{branch\_idx}, \dots, N,\quad \lambda \in \Lambdaxi+1xi+1λ=Axi+Bui,=Axiλ+Bui,i=0,1,…,branch_idx−1i=branch_idx,…,N,λ∈Λ
初始状态约束及 boundary 约束:
这里的 boundary 约束会根据不同的 scene 使用不同的 boundary
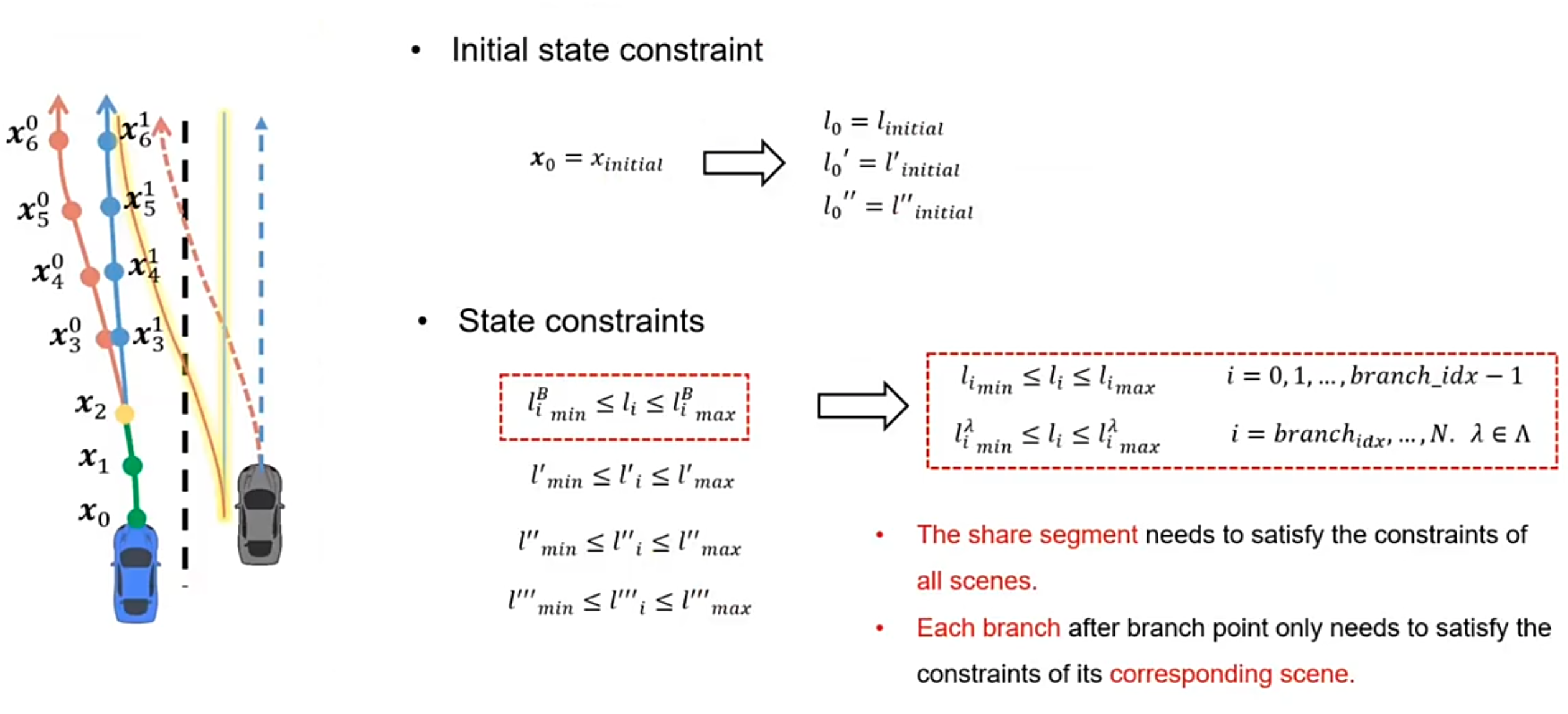
目标函数,约束汇总:
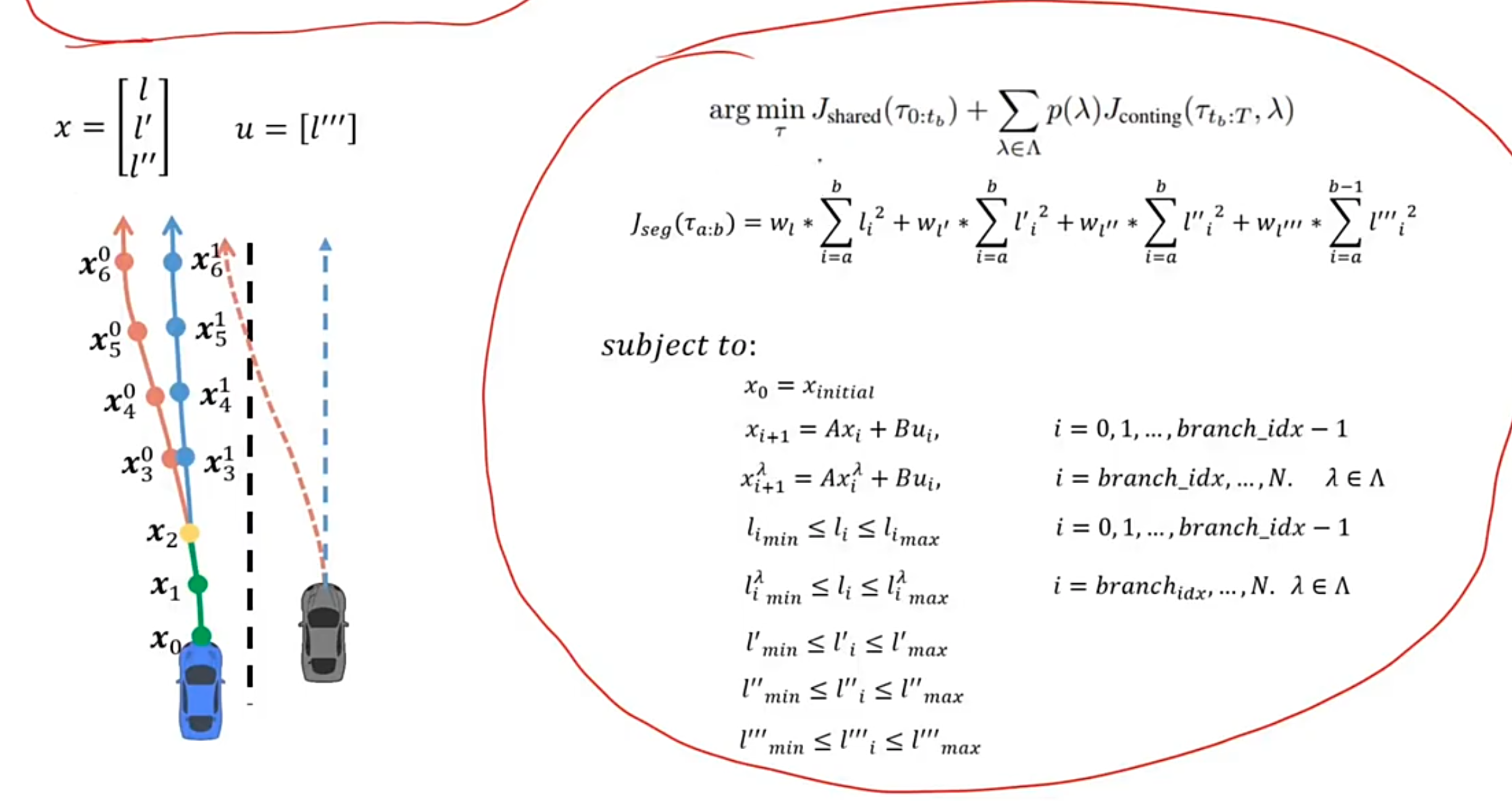
Contingency Speed Planning (ST)
2.iLQR
数学建模
代价函数
x∗,u∗=argminx,u{ϕ(xN)+∑k=0N−1Lk(xk,uk)}s.t.xk+1=fk(xk,uk),k=0,1,…,N−1x0=xstart\begin{aligned} & x^*, u^* = \arg\min_{x,u} \left\{ \phi(x_N) + \sum_{k=0}^{N-1} L^{k}(x_k, u_k) \right\} \\ & \text{s.t.} \quad x_{k+1} = f^{k}(x_k, u_k), \quad k=0,1,\dots,N-1 \\ & x_0 = x_{start} \end{aligned}x∗,u∗=argx,umin{ϕ(xN)+k=0∑N−1Lk(xk,uk)}s.t.xk+1=fk(xk,uk),k=0,1,…,N−1x0=xstart
对于一条轨迹来说,假设有 5 个点 x0−x4x_{0}-x_{4}x0−x4 代表状态值,点与点之间有一个控制量 u0−u3u_{0}-u_{3}u0−u3 也就是转向角度和加速度。iLQR 最终的目标就是优化 ∑k=0N−1Lk(xk,uk)\sum_{k=0}^{N-1}L^{k}(x_k, u_k)∑k=0N−1Lk(xk,uk) xxx 和 uuu
对于终点 xNx_{N}xN 不需要再对它的下一步进行控制,所以没有对应的 uuu ,也就是 uN=0u_N = 0uN=0 所以 ϕ(xN)\phi(x_N)ϕ(xN) 代表终点状态代价
状态转移方程 xk+1=fk(xk,uk)\quad x_{k+1} = f^{k}(x_k, u_k)xk+1=fk(xk,uk) 可以得到下一个目标点的位置
c 代表每一步的目标函数,下面是目标函数的展开:
minu1,…,uTc(x1,u1)+c(f(x1,u1),u2)+⋯+c(f(f(⋯ )),uT)\min_{u_{1}, \dots, u_{T}} c(\mathbf{x}_1, \mathbf{u}_1) + c(f(\mathbf{x}_1, \mathbf{u}_1), \mathbf{u}_2) + \cdots + c(f(f(\cdots)), \mathbf{u}_T)u1,…,uTminc(x1,u1)+c(f(x1,u1),u2)+⋯+c(f(f(⋯)),uT)
x1x_{1}x1 代表起始位置,uuu 代表控制变量。这里的 x2x_2x2 是通过 x2=f(x1,u1)x_2 = f(x_1,u_1)x2=f(x1,u1) 得到的,同理 x3x_3x3 也是由 x1x_1x1 推到来,所以 fff 是相互嵌套的
状态转移方程线性化的表达如下:
f(xt,ut)=Ft[xtut]+ftf(x_t, u_t) = F_t \left[ \begin{array}{c} x_t \\ u_t \end{array} \right] + f_tf(xt,ut)=Ft[xtut]+ft
这是一个线性化的系统动态模型,描述状态如何从t演变到 t+1
FtF_tFt :状态和控制输入的线性变换矩阵
ftf_tft:线性模型的偏置项
c(xt,ut)=12[xtut]⊤Ct[xtut]+[xtut]⊤ctquadraticc(\mathbf{x}_t, \mathbf{u}_t) = \frac{1}{2} \begin{bmatrix} \mathbf{x}_t \\ \mathbf{u}_t \end{bmatrix}^\top
\mathbf{C}_t
\begin{bmatrix} \mathbf{x}_t \\ \mathbf{u}_t \end{bmatrix} + \begin{bmatrix} \mathbf{x}_t \\ \mathbf{u}_t \end{bmatrix}^\top \mathbf{c}_t
\quad \text{quadratic}c(xt,ut)=21[xtut]⊤Ct[xtut]+[xtut]⊤ctquadratic
将目标函数转换为泰勒二次展开式,包含二次项和线性项。在iLQR(迭代线性二次调节器)算法中,将代价函数(或系统动态)转换为二次型(或线性)的核心思想是局部近似。
CT=[CxT,xTCuT,xT,CxT,uTCuT,uT]C_T = \left[ \begin{array}{c} C_{x_T, x_T} \\ C_{u_T, x_T} \end{array}, \begin{array}{c} C_{x_T, u_T} \\ C_{u_T, u_T} \end{array} \right]CT=[CxT,xTCuT,xT,CxT,uTCuT,uT]
CtC_tCt :时间步t的成本函数的二次项系数矩阵(Hessian矩阵)
ctc_tct:时间步t的成本函数的线性项系数向量
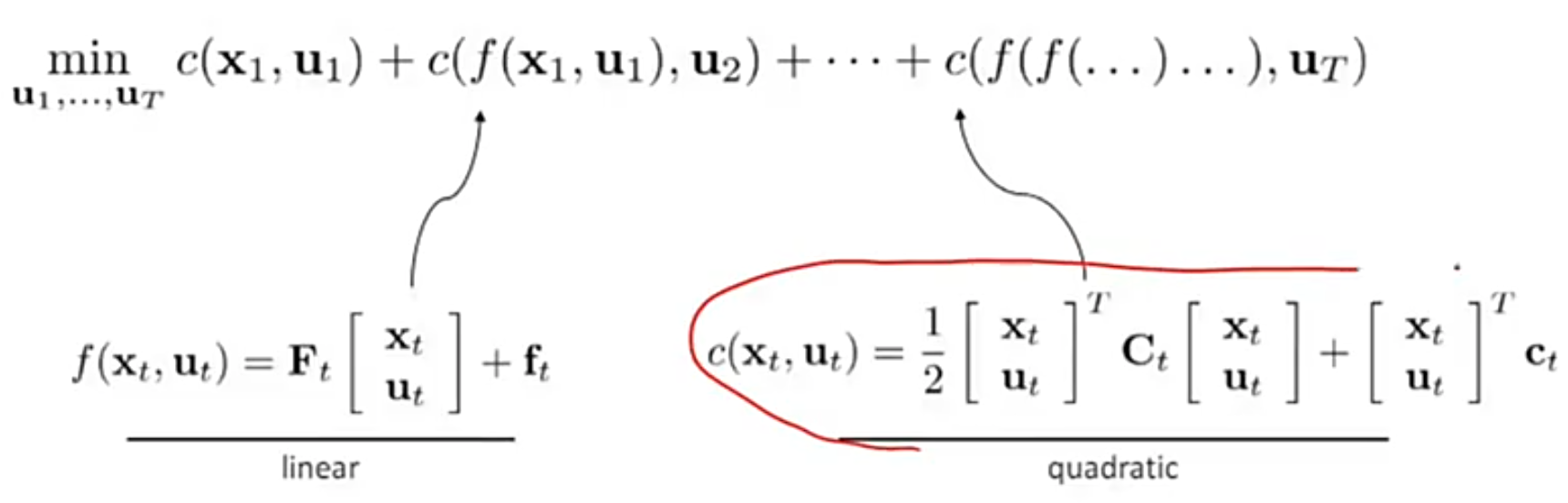
最优控制求解
Q(xT,uT)=const+12[xTuT]⊤CT[xTuT]+[xTuT]⊤cTQ(x_T, u_T) = \text{const} + \frac{1}{2}
\begin{bmatrix}
x_T \\
u_T
\end{bmatrix}^\top
C_T
\begin{bmatrix}
x_T \\
u_T
\end{bmatrix}
+
\begin{bmatrix}
x_T \\
u_T
\end{bmatrix}^\top
c_TQ(xT,uT)=const+21[xTuT]⊤CT[xTuT]+[xTuT]⊤cT
类似强化学习,xxx 看做状态,uuu 看做控制量,将其转换为状态价值函数,也就是在 xTx_{T}xT 时刻采取控制量 uTu_TuT 下的代价加上之后所有时间步长的最优代价之和。const 任何不会影响优化过程的常数偏置。
V(xT)=minuTQ(xT,uT)V(x_T) = \min_{u_T} Q(x_T, u_T)V(xT)=uTminQ(xT,uT)
V(xT)V(x_T)V(xT) 是在 xTx_TxT 下最优策略代价函数,如果这里的 u 取的是最优控制的 u ,那么 V(xT)=minuTQ(xT,uT)V(x_T) = \min_{u_T} Q(x_T, u_T)V(xT)=minuTQ(xT,uT)
求最优控制就是求哪一个 u 可以使得 Q 最小。所以将 u 看做变量 x 看做常数,对 u 求导,当 Q = 0 时求出极值点,公式如下:
∇uTQ(xT,uT)=CuT,xTxT+CuT,uTuT+cuT=0uT=−CuT,uT−1(CuT,xTxT+cuT)\begin{aligned}
& \nabla_{\mathbf{u}_T} Q(\mathbf{x}_T, \mathbf{u}_T) = \mathbf{C}_{u_T, x_T} \mathbf{x}_T + \mathbf{C}_{u_T, u_T} \mathbf{u}_T + \mathbf{c}_{u_T} = 0 \\
& \mathbf{u}_T = - \mathbf{C}^{-1}_{u_T, u_T} \left( \mathbf{C}_{u_T, x_T} \mathbf{x}_T + \mathbf{c}_{u_T} \right)
\end{aligned}∇uTQ(xT,uT)=CuT,xTxT+CuT,uTuT+cuT=0uT=−CuT,uT−1(CuT,xTxT+cuT)
uT=KrxT+kr\mathbf{u}_T = \mathbf{K}_{r} \mathbf{x}_T + \mathbf{k}_{r}uT=KrxT+kr
cT=[cxTcuT]\mathbf{c}_T =
\begin{bmatrix}
\mathbf{c}_{xT} \\
\mathbf{c}_{uT}
\end{bmatrix}cT=[cxTcuT]
KT=−CuT,uT−1CuT,xTkT=−CuT,uT−1cuT\begin{aligned}
\mathbf{K}_T &= - \mathbf{C}^{-1}_{u_T, u_T} \mathbf{C}_{u_T, x_T} \\
\mathbf{k}_T &= - \mathbf{C}^{-1}_{u_T, u_T} \mathbf{c}_{u_T}
\end{aligned}KTkT=−CuT,uT−1CuT,xT=−CuT,uT−1cuT
CTC_TCT 为设计的代价函数系数的矩阵.
KKK 代表反馈项的系数
kkk 代表前馈项的系数
那么将上面 uuu 的结果带入到 QQQ 中就可以得到状态价值函数 V:

将 VVV 的表达式展开得到:
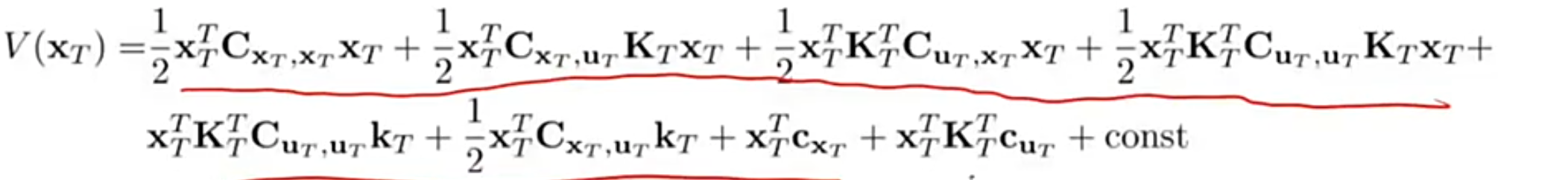
将上面的展开式转换为二次型:
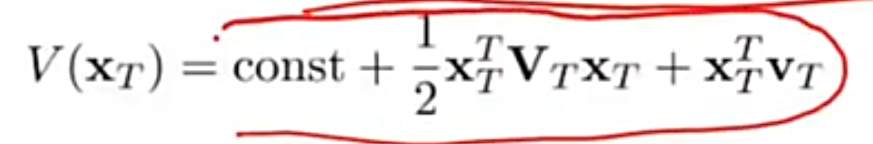
其中 VVV 和 vvv 的表达式为:
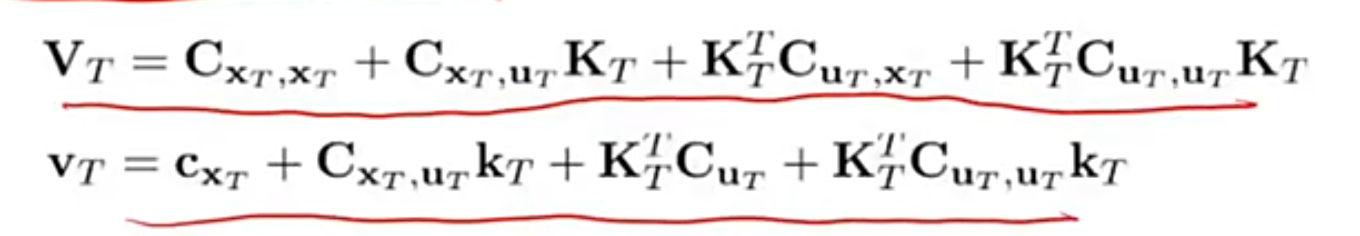
通过上面的计算可以看到我们最终需要计算 V(xT)V(x_T)V(xT) 的值。得到了 VTV_TVT 和 uTu_TuT 就可以算出 VT−1V_{T-1}VT−1
(1)得到 xTx_{T}xT 的值
根据状态转移方程得到下面的公式
f(xT−1,uT−1)=xT=FT−1[xT−1uT−1]+fT−1f(\mathbf{x}_{T-1}, \mathbf{u}_{T-1}) = \mathbf{x}_T = \mathbf{F}_{T-1} \begin{bmatrix} \mathbf{x}_{T-1} \\ \mathbf{u}_{T-1} \end{bmatrix} + \mathbf{f}_{T-1}f(xT−1,uT−1)=xT=FT−1[xT−1uT−1]+fT−1
(2)得到在 T−1T-1T−1 时间下的 Q
该公式包含两个部分,前半部分代表该状态即时价值,也就是强化学习的 RRR ,后半部分代表 V(XT)V(X_{T})V(XT) 的价值
强化学习状态动作价值函数公式:Q(T−1)=R(T−1)+V(T)Q(T-1) = R(T-1)+V(T)Q(T−1)=R(T−1)+V(T)
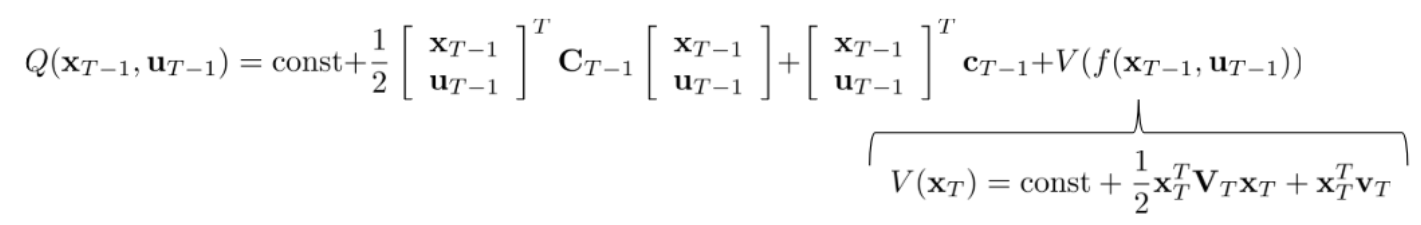
(3)V(xT)V(x_{T})V(xT) 最终公式
Q(T−1)=R(T−1)+V(T)Q(T-1) = R(T-1)+V(T)Q(T−1)=R(T−1)+V(T)
根据上面的计算可以得到 V(xT)V(x_{T})V(xT) 最终二次型公式
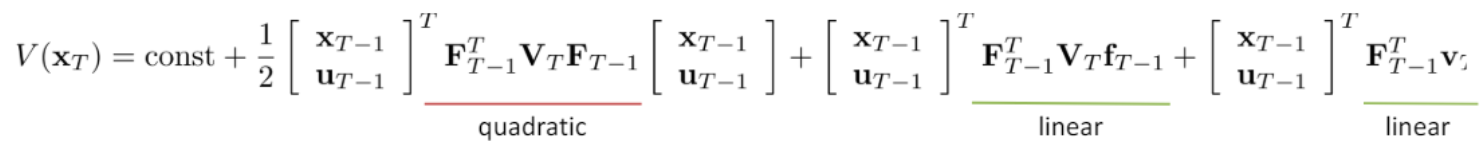

上面就是 iLQR 反馈计算 uuu 的过程
LQR 前馈和反馈步骤
反馈
反馈就是从 T 时刻往后退推到 1 时刻,在这个过程中可以求出 u 的 (k,K)的值
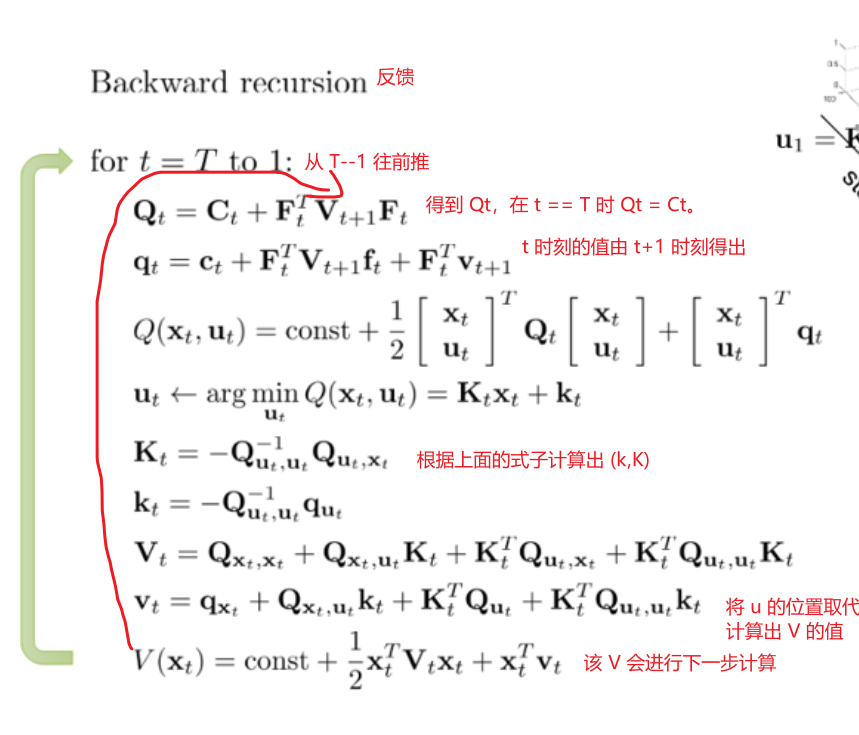
δu∗=argminδuQ(δx,δu)=−Quu−1(Qu+Quxδx)k=−Quu−1QuK=−Quu−1Qux\begin{aligned} \delta \mathbf{u}^* &= \mathop{\arg\min}\limits_{\delta \mathbf{u}} Q(\delta \mathbf{x}, \delta \mathbf{u}) = -\mathbf{Q}_{uu}^{-1}(\mathbf{Q}_u + \mathbf{Q}_{ux}\delta \mathbf{x}) \\ \mathbf{k} &= -\mathbf{Q}_{uu}^{-1}\mathbf{Q}_u \\ \mathbf{K} &= -\mathbf{Q}_{uu}^{-1}\mathbf{Q}_{ux} \end{aligned}δu∗kK=δuargminQ(δx,δu)=−Quu−1(Qu+Quxδx)=−Quu−1Qu=−Quu−1Qux
ΔV(i)=−12Qu⊤Quu−1QuVx(i)=Qx−Qux⊤Quu−1QuVxx(i)=Qxx−Qux⊤Quu−1Qux\begin{aligned} \Delta V(i) &= -\frac{1}{2} \mathbf{Q}_u^\top \mathbf{Q}_{uu}^{-1} \mathbf{Q}_u \\ \mathbf{V}_x(i) &= \mathbf{Q}_x - \mathbf{Q}_{ux}^\top \mathbf{Q}_{uu}^{-1} \mathbf{Q}_u \\ \mathbf{V}_{xx}(i) &= \mathbf{Q}_{xx} - \mathbf{Q}_{ux}^\top \mathbf{Q}_{uu}^{-1} \mathbf{Q}_{ux} \end{aligned}ΔV(i)Vx(i)Vxx(i)=−21Qu⊤Quu−1Qu=Qx−Qux⊤Quu−1Qu=Qxx−Qux⊤Quu−1Qux
前馈
前向传播是从初始状态开始,通过一系列时间步骤生成整个轨迹的过程。有了初始化的 K 的值就可以算 U ,然后在根据状态转移方程计算 x
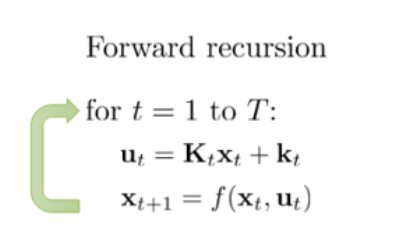
iLQR
iLQR 相当于在 LQR 的基础上进行二次泰勒展开,那么状态转移方程为:
(1)LQR
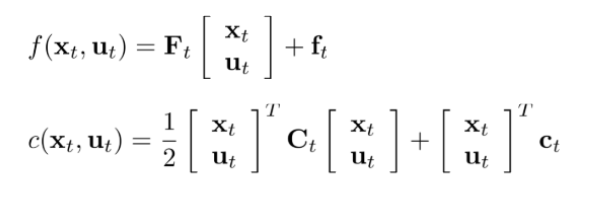
(2)iLQR
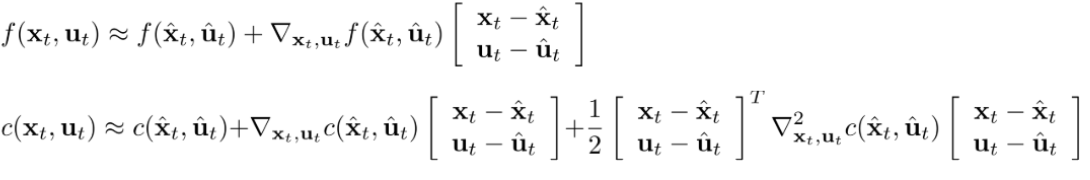
上式中 xhatx_{hat}xhat 代表 xtx_txt 的参考点,那么就可以用参考点的值推算出 xtx_txt 的值。这里 xhatx_{hat}xhat 一般都是用上一个轨迹点。
那么 ILQR 可以理解为计算 δu\delta uδu 的结果
(3)iLQR 的整体流程

x^(1)=x(1)u^(i)=u(i)+k(i)+K(i)(x^(i)−x(i))x^(i+1)=f(x^(i),u^(i))
\begin{aligned}
\hat{\mathbf{x}}(1) &= \mathbf{x}(1) \\
\hat{\mathbf{u}}(i) &= \mathbf{u}(i) + \mathbf{k}(i) + \mathbf{K}(i)\big(\hat{\mathbf{x}}(i) - \mathbf{x}(i)\big) \\
\hat{\mathbf{x}}(i+1) &= \mathbf{f}\big(\hat{\mathbf{x}}(i), \hat{\mathbf{u}}(i)\big)
\end{aligned}
x^(1)u^(i)x^(i+1)=x(1)=u(i)+k(i)+K(i)(x^(i)−x(i))=f(x^(i),u^(i))
常见论文中的推导公式
上面的公式是推导公式,下面是论文中常见的表达
J0(x,U)=∑i=0N−1ℓ(xi,ui)+ℓf(xN),J_0(\mathbf{x}, \mathbf{U}) = \sum_{i=0}^{N-1} \ell(\mathbf{x}_i, \mathbf{u}_i) + \ell_f(\mathbf{x}_N),J0(x,U)=i=0∑N−1ℓ(xi,ui)+ℓf(xN),
整体代价函数为前面每个边的代价 + 终点代价
u∗(x)≡argminuJ0(x,U)\mathbf{u}^*(\mathbf{x}) \equiv \arg\min_{\mathbf{u}} J_0(\mathbf{x}, \mathbf{U})u∗(x)≡arguminJ0(x,U)
最优控制问题就是想求代价最小找到最优控制量 UUU
V(x,i)=minu[ℓ(x,u)+V(f(x,u),i+1)]V(\mathbf{x}, i) = \min_{\mathbf{u}} \left[ \ell(\mathbf{x}, \mathbf{u}) + V(f(\mathbf{x}, \mathbf{u}), i+1) \right]V(x,i)=umin[ℓ(x,u)+V(f(x,u),i+1)]
上面公式为 Cost-to-go function,该值等于当前状态的代价 + 往后一步的代价。
对于 iLQR 的目标函数表达为:
Q(δx,δu)=ℓ(x+δx,u+δu,i)+V(f(x+δx,u+δu),i+1)−V(f(x,u),i+1)
Q(\delta x, \delta u) = \ell(x + \delta x, u + \delta u, i) + V(f(x + \delta x, u + \delta u), i + 1) - V(f(x, u), i + 1)
Q(δx,δu)=ℓ(x+δx,u+δu,i)+V(f(x+δx,u+δu),i+1)−V(f(x,u),i+1)
≈12[1δxδu]T[0QxTQuTQxQxxQxuQuQuxQuu][1δxδu]\approx \frac{1}{2}
\begin{bmatrix}
1 \\
\delta x \\
\delta u
\end{bmatrix}^T
\begin{bmatrix}
0 & Q_x^T & Q_u^T \\
Q_x & Q_{xx} & Q_{xu} \\
Q_u & Q_{ux} & Q_{uu}
\end{bmatrix}
\begin{bmatrix}
1 \\
\delta x \\
\delta u
\end{bmatrix}≈211δxδuT0QxQuQxTQxxQuxQuTQxuQuu1δxδu
上面公式求得就是 δx,δu\delta x, \delta uδx,δu 的代价,这两个是基于 x,u 的增量,含义就是添加增量后的代价 - 没有添加增量时的代价
Qx=lx+fx⊤Vx′Qu=lu+fu⊤Vx′Qxx=lxx+fx⊤Vxx′fx+Vx′⋅fxxQuu=luu+fu⊤Vxx′fu+Vx′⋅fuuQux=lux+fu⊤Vxx′fx+Vx′⋅fux \begin{aligned} Q_x &= l_x + f_x^\top V_x' \\ Q_u &= l_u + f_u^\top V_x' \\ Q_{xx} &= l_{xx} + f_x^\top V_{xx}' f_x + V_x' \cdot f_{xx} \\ Q_{uu} &= l_{uu} + f_u^\top V_{xx}' f_u + V_x' \cdot f_{uu} \\ Q_{ux} &= l_{ux} + f_u^\top V_{xx}' f_x + V_x' \cdot f_{ux} \end{aligned} QxQuQxxQuuQux=lx+fx⊤Vx′=lu+fu⊤Vx′=lxx+fx⊤Vxx′fx+Vx′⋅fxx=luu+fu⊤Vxx′fu+Vx′⋅fuu=lux+fu⊤Vxx′fx+Vx′⋅fux
iLQR 在 Contingency Planning 的使用
(1)反馈
对于 tree model 来说在计算 Q 时只需要将每个 branch 的 Q 乘一个系数再进行累加
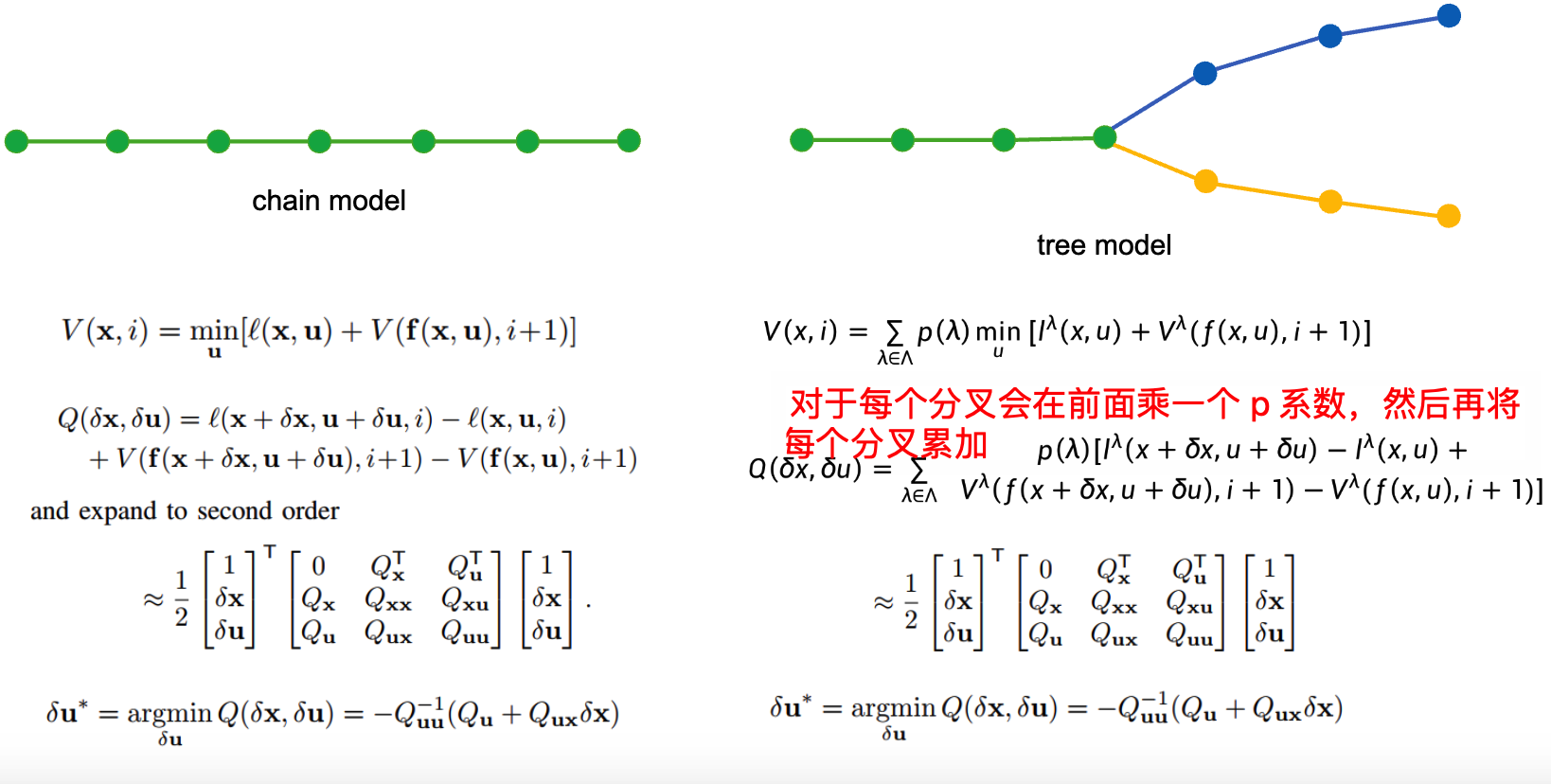
(2)前馈
对于前馈来说每一个点都会计算出一个 (k,K) 那么改点根据自己的 (k,K) 的值生成轨迹
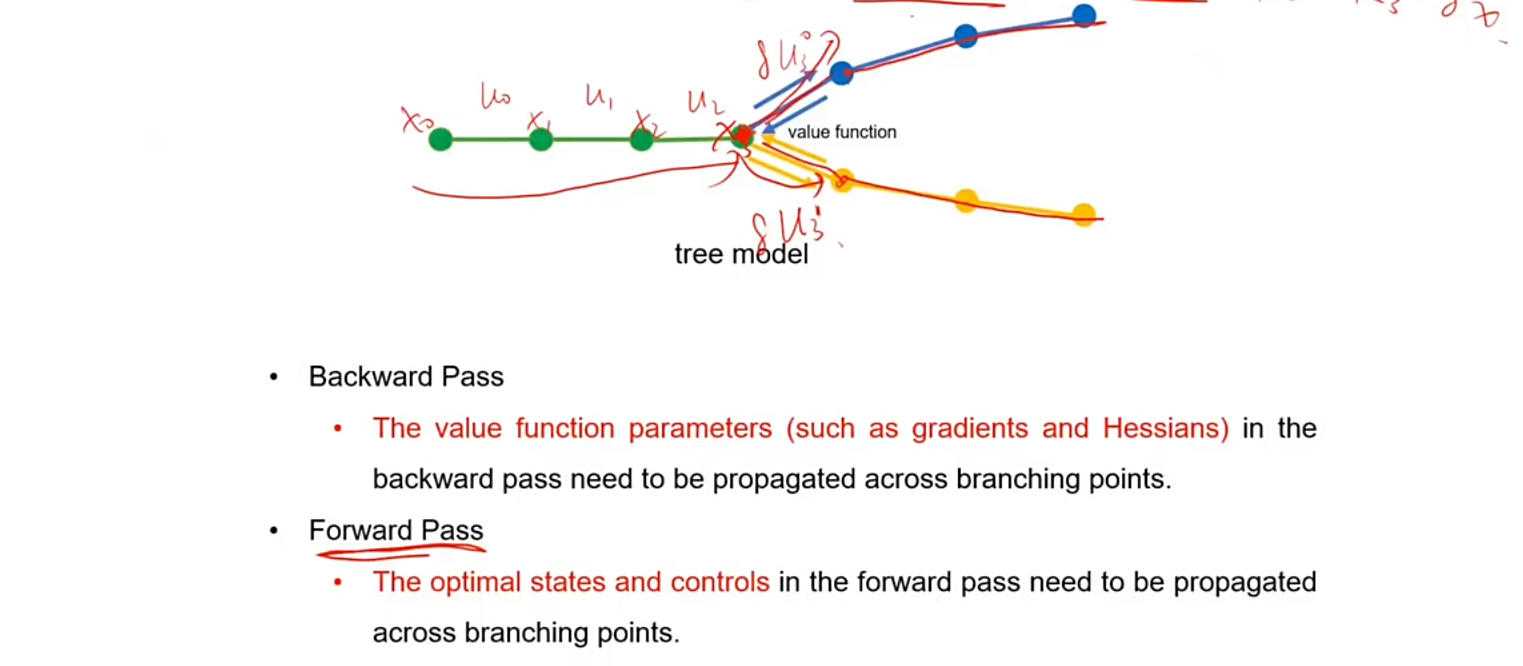
Risk-Aware Contingency Planning
RACP: Risk-Aware Contingency Planning with Multi-Modal Predictions
1.Collision Chance Constraints
这里是根据自车和障碍物之间的距离计算出来的碰撞概率
P(∥xkv−δko∥≤r)≤1−δ\mathbb{P}\big(\|x_{k}^{v} - \delta_{k}^{o}\| \leq r\big) \leq 1 - \deltaP(∥xkv−δko∥≤r)≤1−δ
对于上式来说,xkvx_{k}^{v}xkv 代表自车当前位置,δko\delta_{k}^{o}δko 代表目标车的位置
风险概率的定义:
Rko(xkd)=Cko(xkd)Sko(xkd),∀k,o,d\mathcal{R}_{k}^{o} \left( x_{k}^{d} \right) = \mathcal{C}_{k}^{o} \left( x_{k}^{d} \right) \mathcal{S}_{k}^{o} \left( x_{k}^{d} \right), \quad \forall k, o, dRko(xkd)=Cko(xkd)Sko(xkd),∀k,o,d
上式中 Rko{R}_{k}^{o}Rko 代表风险概率,Cko{C}_{k}^{o}Cko 代表碰撞的风险,Sko{S}_{k}^{o}Sko 代表碰撞后的严重程度,其中 C 的计算和 S 的计算如下所示:
Cko(xkd)=∬(xkd,ykd)∈Dfko(x,y) dx dy,∀k,o,dC_{k}^{o}\left(\boldsymbol{x}_{k}^{d}\right) = \iint\limits_{(\boldsymbol{x}_{k}^{d}, y_{k}^{d}) \in D} f_{k}^{o}(\boldsymbol{x}, \boldsymbol{y}) \, d\boldsymbol{x}\, d\boldsymbol{y}, \quad \forall k, o, dCko(xkd)=(xkd,ykd)∈D∬fko(x,y)dxdy,∀k,o,d
C 的计算使用碰撞概率密度的积分得到的。
Sko(xkd)=mvmv+mo((vkv)2+(vko)2−2vkvvkocosα)12S_k^o \left( x_k^d \right) = \frac{m^v}{m^v + m^o} \left( \left( v_k^v \right)^2 + \left( v_k^o \right)^2 - 2 v_k^v v_k^o \cos \alpha \right)^{\frac{1}{2}}Sko(xkd)=mv+momv((vkv)2+(vko)2−2vkvvkocosα)21

对于一条轨迹远处的点风险更小,近处的点风险更大更应该关注,所以下面的公式在每个点中乘了一个概率表现每个点的重要程度
Rko(xkd)=(γ)k Cko(xkd) Sko(xkd),∀k,o,d\mathcal{R}_{k}^{o} \left( \boldsymbol{x}_{k}^{d} \right) = \left( \gamma \right)^{k} \, \mathcal{C}_{k}^{o} \left( \boldsymbol{x}_{k}^{d} \right) \, \mathcal{S}_{k}^{o} \left( \boldsymbol{x}_{k}^{d} \right), \quad \forall k, o, dRko(xkd)=(γ)kCko(xkd)Sko(xkd),∀k,o,d
3.Game Theory Based Interactive Planning
iLQGame
iLQR 和 iLQGame 的区别
iLQR 在进行多 agent 迭代时是非常耗时的,如下图所示当存在多个 agent 时,当求 agent 1 时需要将 agent 2,agent 3 状态固定,求 agengt 2 时需要将 agent1 agent2 状态固定,迭代的求不同 agent 的轨迹。
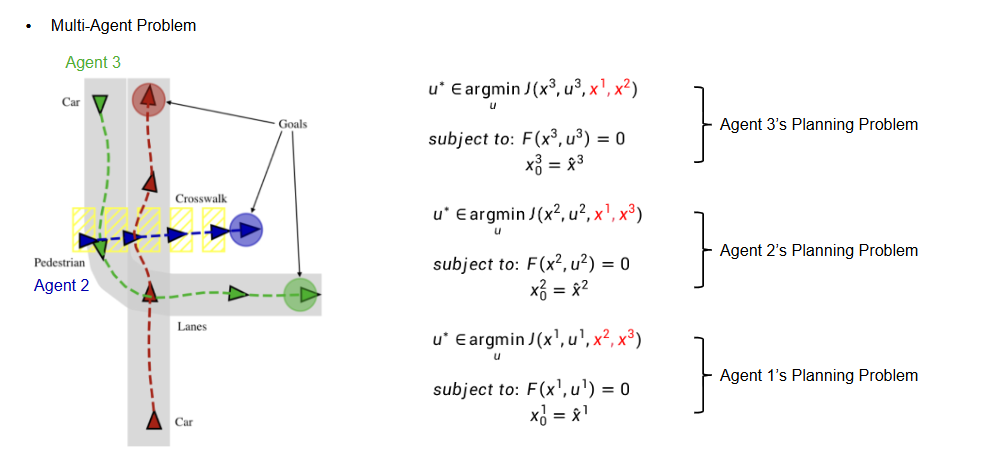
iLQGame 就是将所有 agent 的求解都放到一个公式中
动力学方程:
x˙=f(t,x,u1:N)\dot{\boldsymbol{x}} = \boldsymbol{f}(t, \boldsymbol{x}, \boldsymbol{u}_{1:N})x˙=f(t,x,u1:N)
x=[x1y1v1θ1x2y2v2θ2x3y3v3θ3]x = \left [ \begin{matrix}
\\x1
\\y1
\\v1
\\\theta 1
\\x2
\\y2
\\v2
\\\theta 2
\\x3
\\y3
\\v3
\\\theta 3
\end{matrix} \right ] x=x1y1v1θ1x2y2v2θ2x3y3v3θ3
x 是多个子系统状态的联合状态向量(concatenated states)假设这里有 3 辆车,例如多辆车的联合状态(位置、速度等)。u表示所有玩家(如 N 辆车)的联合控制输入。f 是非线性函数,描述状态如何随时间演化(如车辆动力学)。
代价函数:
Ji(u1:N(⋅))≜∫0Tgi(t,x(t),u1:N(t)) dtJ_i(\mathbf{u}_{1:N}(\cdot)) \triangleq \int_{0}^{T} g_i\big(t, \mathbf{x}(t), \mathbf{u}_{1:N}(t)\big) \, dtJi(u1:N(⋅))≜∫0Tgi(t,x(t),u1:N(t))dt
J=J1+J2+J3J = J_1+J_2+J_3J=J1+J2+J3
每个玩家 i 有自己的成本函数 JiJ_{i}Ji ,成本的公式为 gig_{i}gi ,最后所有玩家的目标函数累加求 u (假设这里有 3 个玩家)。其中 g 可以代表一条轨迹的平滑度,与其他轨迹的碰撞风险等 cost 。
如下图所示车和人的动态方程如下,也就是下一步各子状态的增益,根据目标动态方程可以计算出目标函数也就是 Objectives 下的公式
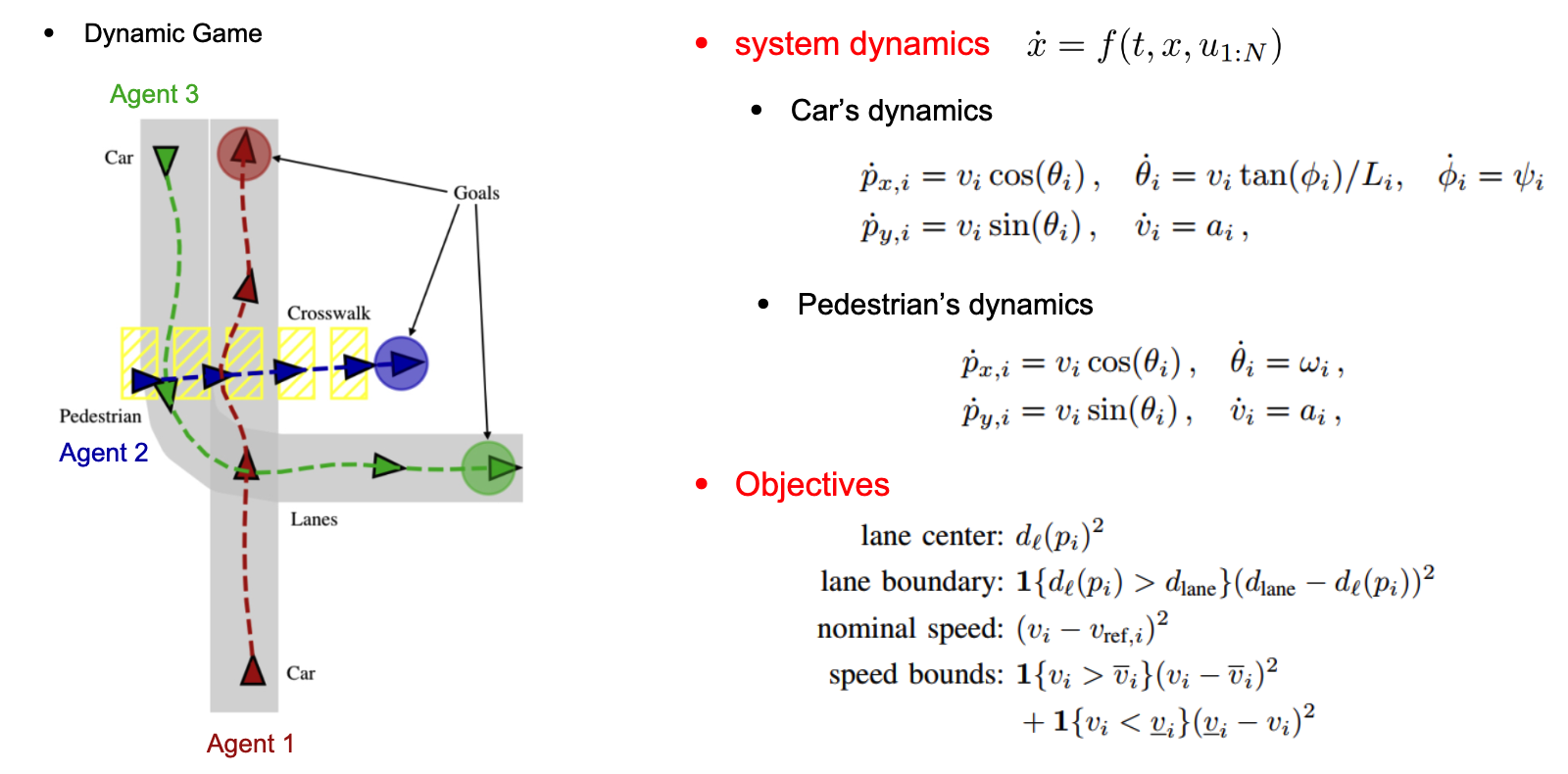
目标–纳什均衡
Ji∗≜Ji(γ1∗,…,γi−1∗,γi∗,γi+1∗,…,γN∗)≤Ji(γ1∗,…,γi−1∗,γi,γi+1∗,…,γN∗),∀i∈[N]\begin{aligned}
J_{i}^{*} &\triangleq J_{i}(\gamma_{1}^{*}, \ldots, \gamma_{i-1}^{*}, \gamma_{i}^{*}, \gamma_{i+1}^{*}, \ldots, \gamma_{N}^{*}) \\
&\leq J_{i}(\gamma_{1}^{*}, \ldots, \gamma_{i-1}^{*}, \gamma_{i}, \gamma_{i+1}^{*}, \ldots, \gamma_{N}^{*}), \quad \forall i \in [N]
\end{aligned}Ji∗≜Ji(γ1∗,…,γi−1∗,γi∗,γi+1∗,…,γN∗)≤Ji(γ1∗,…,γi−1∗,γi,γi+1∗,…,γN∗),∀i∈[N]
目标是找到每个玩家的时变状态反馈策略 γi∗\gamma_{i}^{*}γi∗,使得在纳什均衡下,任何玩家单方面偏离策略 γi\gamma_{i}γi 都无法降低自己的成本。
这个 γi∗\gamma_{i}^{*}γi∗ 和 ui∗u_{i}^{*}ui∗ 类似,在求 u∗u^{*}u∗ 时 u∗=k+KΔxu^{*}=k+K\Delta xu∗=k+KΔx,γi∗=α+PΔx\gamma_{i}^{*}=α+P\Delta xγi∗=α+PΔx
在自动驾驶中,每辆车根据其他车的策略(如变道、加速)选择最优反馈控制(如跟车或避让)。
均衡时,所有玩家的策略互为最优响应(Best Response)
数学推导:
将转移方程线性化表示:
xt+1=Atxt+∑j=1NBtjutj\begin{aligned}
\mathbf{x}_{t+1} = \mathbf{A}_t \mathbf{x}_t + \sum_{j=1}^N \mathbf{B}_t^j \mathbf{u}_t^j
\end{aligned}xt+1=Atxt+j=1∑NBtjutj

在 uuu 的前面为什么还有一个累加的符号,并不是将其他 agent 的 uuu 也累加到自车,是因为 B 是一个分块矩阵,当计算 agent1 时其他 agent 的系数是 0,这里最终累加的只有自己的 uuu
Ji=12∑t=1T[(xt⊤Qti+2qti⊤)xt+∑j=1N(utj⊤Rtij+2rtij⊤)utj]J^i = \frac{1}{2}\sum_{t=1}^T \left[
(\mathbf{x}_t^\top \mathbf{Q}_t^i + 2\mathbf{q}_t^{i\top}) \mathbf{x}_t +
\sum_{j=1}^N (\mathbf{u}_t^{j\top} \mathbf{R}_t^{ij} + 2\mathbf{r}_t^{ij\top}) \mathbf{u}_t^j
\right]Ji=21t=1∑T[(xt⊤Qti+2qti⊤)xt+j=1∑N(utj⊤Rtij+2rtij⊤)utj]

求解器:
求解在 t 时刻的最优价值函数
Qti(xt,ut)=minuti{12((xtTQti+2qtiT)xt+∑j=1N(utjTRtij+2rtijT)utj)+Vt+1i(xt+1)}=minuti{12((xtTQti+2qtiT)xt+∑j=1N(utjTRtij+2rtijT)utj)+Vt+1i(Atxt+∑j=1NBtjutj)},\begin{align*}
Q_t^i(x_t,u_t) &= \min_{u_t^i} \left\{ \frac{1}{2}\Big( (x_t^T Q_t^i + 2q_t^{iT}) x_t + \sum_{j=1}^N \big( u_t^{jT} R_t^{ij} + 2r_t^{ijT} \big) u_t^j \Big) + V_{t+1}^i(x_{t+1}) \right\} \\
&= \min_{u_t^i} \left\{ \frac{1}{2}\Big( (x_t^T Q_t^i + 2q_t^{iT}) x_t + \sum_{j=1}^N \big( u_t^{jT} R_t^{ij} + 2r_t^{ijT} \big) u_t^j \Big) + V_{t+1}^i \Big( A_t x_t + \sum_{j=1}^N B_t^j u_t^j \Big) \right\},
\end{align*}Qti(xt,ut)=utimin{21((xtTQti+2qtiT)xt+j=1∑N(utjTRtij+2rtijT)utj)+Vt+1i(xt+1)}=utimin{21((xtTQti+2qtiT)xt+j=1∑N(utjTRtij+2rtijT)utj)+Vt+1i(Atxt+j=1∑NBtjutj)},
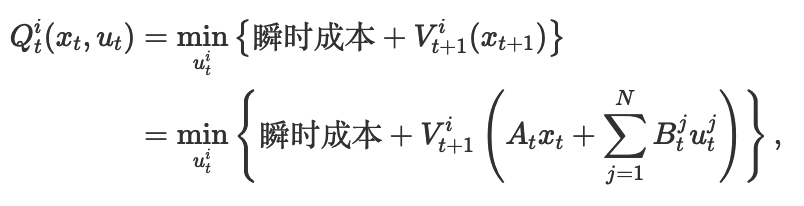
转换为价值函数如下:
Vti(xt)=12(xtTZti+2ζtiT)xt+nti,(5)V_{t}^{i}(x_{t}) = \frac{1}{2} \left( x_{t}^{T} Z_{t}^{i} + 2 \zeta_{t}^{iT} \right) x_{t} + n_{t}^{i},
\tag{5}Vti(xt)=21(xtTZti+2ζtiT)xt+nti,(5)

将上面的 Q 公式中值替换为 V 的表达式如下:
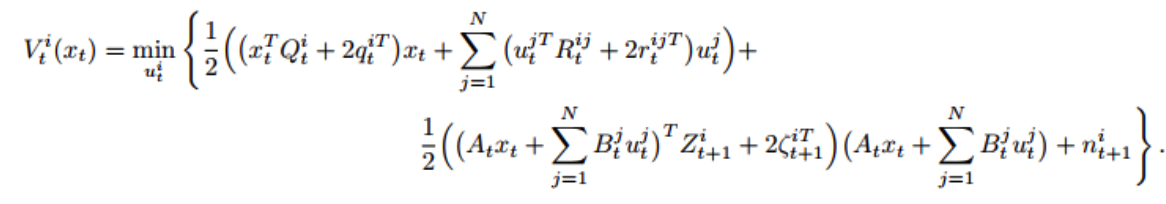
根据上面的公式对第 i 个 agent 进行求导,也就是对 dutid^{t}_uiduti 进行求导
0=Rtiiuti+rtii+Bti⊤Zt+1i(Atxt+∑j=1NBtjutj)+Bti⊤ζt+1i.\begin{align*}
0 = R_t^{ii} u^i_t + r_t^{ii} + B_t^{i\top} Z_{t+1}^i \left( A_t x_t + \sum_{j=1}^N B_t^j u_t^j \right) + B_t^{i\top} \zeta_{t+1}^i.
\end{align*}0=Rtiiuti+rtii+Bti⊤Zt+1i(Atxt+j=1∑NBtjutj)+Bti⊤ζt+1i.

求得最优控制量最终表达形式如下:
uti∗=−Ptixt−αti.\begin{align*}
u_t^{i*} = -P_t^i x_t - \alpha_t^i.
\end{align*}uti∗=−Ptixt−αti.

最终目的就是求 P 和 α 的值。这 u 的表达式放在求导的表达式中:
0=−Rtii(Ptixt+αti)+rtii+Bti⊤Zt+1i(Atxt−∑j=1NBtj(Ptjxt+αtj))+Bti⊤ζt+1i.\begin{align*}
0 = &-R_t^{ii} \left( P_t^i x_t + \alpha_t^i \right) + r_t^{ii} \\
&+ B_t^{i\top} Z_{t+1}^i \left( A_t x_t - \sum_{j=1}^N B_t^j \left( P_t^j x_t + \alpha_t^j \right) \right) \\
&+ B_t^{i\top} \zeta_{t+1}^i.
\end{align*}0=−Rtii(Ptixt+αti)+rtii+Bti⊤Zt+1i(Atxt−j=1∑NBtj(Ptjxt+αtj))+Bti⊤ζt+1i.
将 x 单独提出后:
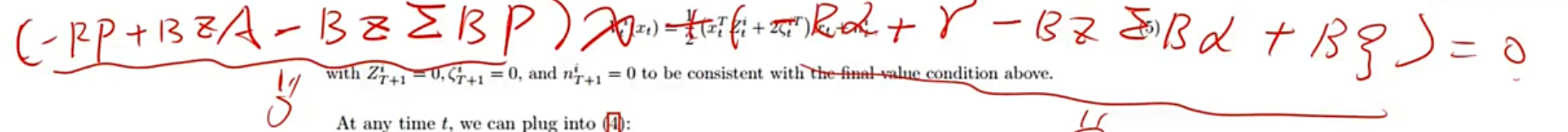
对于上面的公式假设两个子公式的值都是 0。那么分别求出 P 和 α 的表达式:
(Rtii+Bti⊤Zt+1iBti)Pti+Bti⊤Zt+1i∑j≠iBtjPtj=Bti⊤Zt+1iAt,(Rtii+Bti⊤Zt+1iBti)αti+Bti⊤Zt+1i∑j≠iBtjαtj=Bti⊤ζt+1i+rtii.\begin{align*}
\left(R_t^{ii} + B_t^{i\top} Z_{t+1}^i B_t^i\right) P_t^i + B_t^{i\top} Z_{t+1}^i \sum_{j \neq i} B_t^j P_t^j &= B_t^{i\top} Z_{t+1}^i A_t, \\
\left(R_t^{ii} + B_t^{i\top} Z_{t+1}^i B_t^i\right) \alpha_t^i + B_t^{i\top} Z_{t+1}^i \sum_{j \neq i} B_t^j \alpha_t^j &= B_t^{i\top} \zeta_{t+1}^i + r_t^{ii}.
\end{align*}(Rtii+Bti⊤Zt+1iBti)Pti+Bti⊤Zt+1ij=i∑BtjPtj(Rtii+Bti⊤Zt+1iBti)αti+Bti⊤Zt+1ij=i∑Btjαtj=Bti⊤Zt+1iAt,=Bti⊤ζt+1i+rtii.

由于 BBB,ZZZ 都是已知变量,那么在求 PPP 和 ααα 矩阵时可以转换成求 SX=YSX = YSX=Y 的形式,其中 S,YS,YS,Y 都是已知矩阵。最后的 P,αP,αP,α 就是 XXX


通过上面步骤求出了 u,将 u 带入 Q(x,u) 中可以得到 V(x) 的表达式:
Vti(xt)=12((xt⊤Qti+2qti⊤)xt+∑j=1N((Ptjxt+αtj)⊤Rtij−2rtij⊤)(Ptjxt+αtj))+12((Atxt−∑j=1NBtj(Ptjxt+αtj))⊤Zt+1i+2ζt+1i⊤)(Atxt−∑j=1NBtj(Ptjxt+αtj))+nt+1i=12xt⊤[Qti+∑j=1NPtj⊤RtijPtj+(At−∑j=1NBtjPtj)⊤Zt+1i(At−∑j=1NBtjPtj)]xt+12[qti+∑j=1N(Ptj⊤Rtijαtj−Ptj⊤rtij)+(At−∑j=1NBtjPtj)⊤(ζt+1i−Zt+1i∑j=1NBtjαtj)]xt+12[∑j=1N(αtj⊤Rtij−2rtij⊤)αtj−(2ζt+1i−Zt+1i∑j=1NBtjαtj)⊤∑j=1NBtjαtj]+nt+1i.\begin{align*} V_t^i(x_t) &= \frac{1}{2} \left( (x_t^\top Q_t^i + 2q_t^{i\top}) x_t + \sum_{j=1}^N \left( (P_t^j x_t + \alpha_t^j)^\top R_t^{ij} - 2r_t^{ij\top} \right)(P_t^j x_t + \alpha_t^j) \right) \\ &\quad + \frac{1}{2} \left( \left(A_t x_t - \sum_{j=1}^N B_t^j (P_t^j x_t + \alpha_t^j)\right)^\top Z_{t+1}^i + 2\zeta_{t+1}^{i\top} \right) \left(A_t x_t - \sum_{j=1}^N B_t^j (P_t^j x_t + \alpha_t^j)\right) \\ &\quad + n_{t+1}^i \\ &= \frac{1}{2} x_t^\top \left[ Q_t^i + \sum_{j=1}^N P_t^{j\top} R_t^{ij} P_t^j + \left( A_t - \sum_{j=1}^N B_t^j P_t^j \right)^\top Z_{t+1}^i \left( A_t - \sum_{j=1}^N B_t^j P_t^j \right) \right] x_t \\ &\quad + \frac{1}{2} \left[ q_t^i + \sum_{j=1}^N \left( P_t^{j\top} R_t^{ij} \alpha_t^j - P_t^{j\top} r_t^{ij} \right) + \left( A_t - \sum_{j=1}^N B_t^j P_t^j \right)^\top \left( \zeta_{t+1}^i - Z_{t+1}^i \sum_{j=1}^N B_t^j \alpha_t^j \right) \right] x_t \\ &\quad + \frac{1}{2} \left[ \sum_{j=1}^N (\alpha_t^{j\top} R_t^{ij} - 2r_t^{ij\top}) \alpha_t^j - \left( 2\zeta_{t+1}^i - Z_{t+1}^i \sum_{j=1}^N B_t^j \alpha_t^j \right)^\top \sum_{j=1}^N B_t^j \alpha_t^j \right] \\ &\quad + n_{t+1}^i. \end{align*}Vti(xt)=21((xt⊤Qti+2qti⊤)xt+j=1∑N((Ptjxt+αtj)⊤Rtij−2rtij⊤)(Ptjxt+αtj))+21(Atxt−j=1∑NBtj(Ptjxt+αtj))⊤Zt+1i+2ζt+1i⊤(Atxt−j=1∑NBtj(Ptjxt+αtj))+nt+1i=21xt⊤Qti+j=1∑NPtj⊤RtijPtj+(At−j=1∑NBtjPtj)⊤Zt+1i(At−j=1∑NBtjPtj)xt+21qti+j=1∑N(Ptj⊤Rtijαtj−Ptj⊤rtij)+(At−j=1∑NBtjPtj)⊤(ζt+1i−Zt+1ij=1∑NBtjαtj)xt+21j=1∑N(αtj⊤Rtij−2rtij⊤)αtj−(2ζt+1i−Zt+1ij=1∑NBtjαtj)⊤j=1∑NBtjαtj+nt+1i.
那么就像前面的公式将其转换为 Z,ζZ,\zetaZ,ζ 表示为:
Ft=At−∑j=1NBtjPtj\begin{align*}
F_t = A_t - \sum_{j=1}^N B_t^j P_t^j
\end{align*}Ft=At−j=1∑NBtjPtj
βt=−∑j=1NBtjαtj
\beta_t = - \sum_{j=1}^N B_t^j \alpha_t^j
βt=−j=1∑NBtjαtj
Zti=Qti+∑j=1NPtj⊤RtijPtj+Ft⊤Zt+1iFt,ZT+1i=0,ζti=qti+∑j=1N(Ptj⊤Rtijαtj−Ptj⊤rtij)+Ft⊤(ζt+1i+Zt+1iβt),ζT+1i=0,nti=12[∑j=1N(αtj⊤Rtijαtj−2rtij⊤αtj)−(2ζt+1i−Zt+1i∑j=1NBtjαtj)⊤∑j=1NBtjαtj]+nt+1i,nT+1i=0.\begin{align*}
Z_t^i &= Q_t^i + \sum_{j=1}^N P_t^{j\top} R_t^{ij} P_t^j + F_t^\top Z_{t+1}^i F_t, \quad Z_{T+1}^i = 0, \\
\zeta_t^i &= q_t^i + \sum_{j=1}^N \left( P_t^{j\top} R_t^{ij} \alpha_t^j - P_t^{j\top} r_t^{ij} \right) + F_t^\top \left( \zeta_{t+1}^i + Z_{t+1}^i \beta_t \right), \quad \zeta_{T+1}^i = 0, \\
n_t^i &= \frac{1}{2} \left[ \sum_{j=1}^N \left( \alpha_t^{j\top} R_t^{ij} \alpha_t^j - 2 r_t^{ij\top} \alpha_t^j \right) - \left( 2 \zeta_{t+1}^i - Z_{t+1}^i \sum_{j=1}^N B_t^j \alpha_t^j \right)^\top \sum_{j=1}^N B_t^j \alpha_t^j \right] + n_{t+1}^i, \quad n_{T+1}^i = 0.
\end{align*}Ztiζtinti=Qti+j=1∑NPtj⊤RtijPtj+Ft⊤Zt+1iFt,ZT+1i=0,=qti+j=1∑N(Ptj⊤Rtijαtj−Ptj⊤rtij)+Ft⊤(ζt+1i+Zt+1iβt),ζT+1i=0,=21j=1∑N(αtj⊤Rtijαtj−2rtij⊤αtj)−(2ζt+1i−Zt+1ij=1∑NBtjαtj)⊤j=1∑NBtjαtj+nt+1i,nT+1i=0.
在上面的公式中 agent j 对 agent i 的 u 影响几乎可以看做没有,所以可以将这些值看做 0 ,那么公式可以简化如下:
Z=Q+F⊤ZF,ζ=q+F⊤(ζt+1+Zt+1+β)\begin{align*} Z &= Q + F_{}^\top Z F, \\ \zeta &= q + F^\top (\zeta_{t+1} + Z_{ t+1} + \beta) \end{align*}Zζ=Q+F⊤ZF,=q+F⊤(ζt+1+Zt+1+β)
iLQGame 整体流程:

backward 相关代码
backward 是从后往前计算
for (int kk = num_time_steps_ - 2; kk >= 0; kk--) {
得到线性矩阵和二次型矩阵:


const auto& lin = linearization[kk];
const auto& quad = quadraticization[kk];
上面有说最终求解的是公式 SX=YSX = YSX=Y 那么就要构建每个 agent 的 SYSYSY 矩阵
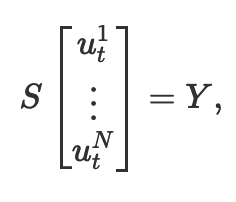
在数学推导章节需要计算每一个 agent 和其他 agent 的 SSS

Dimension cumulative_udim_row = 0;
for (PlayerIndex ii = 0; ii < dynamics_->NumPlayers(); ii++) {
// // Check Nash existence condition (sufficient, not necessary).
// Eigen::LLT<MatrixXf> llt(quad[ii].control.find(ii)->second.hess +
// lin.Bs[ii].transpose() * Zs_[ii] *
// lin.Bs[ii]);
// CHECK(llt.info() != Eigen::NumericalIssue);
// Intermediate variable to store B[ii]' * Z[ii].
// 因为公式中有很多 BiZi 的计算,所以先计算出来
const MatrixXf BiZi = lin.Bs[ii].transpose() * Zs_[kk + 1][ii];
Dimension cumulative_udim_col = 0;
// 填充 S 矩阵
for (PlayerIndex jj = 0; jj < dynamics_->NumPlayers(); jj++) {
Eigen::Ref<MatrixXf> S_block =
S_.block(cumulative_udim_row, cumulative_udim_col,
dynamics_->UDim(ii), dynamics_->UDim(jj));
// 填充 S 矩阵时分为对角和非对角的情况
if (ii == jj) {
// Does player ii's cost depend upon player jj's control?
const auto control_iter = quad[ii].control.find(ii);
CHECK(control_iter != quad[ii].control.end())
<< "Player " << ii << " is missing a control Hessian.";
// BiZiBi+Rii
S_block = BiZi * lin.Bs[ii] + control_iter->second.hess;
} else {
// BiZiBj
S_block = BiZi * lin.Bs[jj];
}
// Increment cumulative_udim_col.
cumulative_udim_col += dynamics_->UDim(jj);
}
// Set appropriate blocks of Y.
// Y 的第一列
Y_.block(cumulative_udim_row, 0, dynamics_->UDim(ii), dynamics_->XDim()) =
BiZi * lin.A;
// Y 的第二列
Y_.col(dynamics_->XDim())
.segment(cumulative_udim_row, dynamics_->UDim(ii)) =
lin.Bs[ii].transpose() * zetas_[kk + 1][ii] +
quad[ii].control.at(ii).grad;
// Increment cumulative_udim_row.
cumulative_udim_row += dynamics_->UDim(ii);
}
// 对 S 进行修改,自适应正则化(确保S矩阵正定)
if (adaptive_regularization_) {
// Regularize `S` to have positive eigenvalues using the Gershgorin circle
// theorem (https://en.wikipedia.org/wiki/Gershgorin_circle_theorem). That
// is, for column i, compute the 1-norm of non-diagonal entries and ensure
// that the ii^th entry of `S` is greater than that norm by adding some
// amount to that diagonal entry.
for (size_t ii = 0; ii < S_.cols(); ii++) {
const float radius = S_.col(ii).lpNorm<1>() - std::abs(S_(ii, ii));
const float eval_lo = S_(ii, ii) - radius;
constexpr float min_eval = 1e-3;
if (eval_lo < min_eval) S_(ii, ii) += radius + min_eval;
}
}
求解 SX=YSX = YSX=Y
// 对 S 进行修改,自适应正则化(确保S矩阵正定)
if (adaptive_regularization_) {
// Regularize `S` to have positive eigenvalues using the Gershgorin circle
// theorem (https://en.wikipedia.org/wiki/Gershgorin_circle_theorem). That
// is, for column i, compute the 1-norm of non-diagonal entries and ensure
// that the ii^th entry of `S` is greater than that norm by adding some
// amount to that diagonal entry.
for (size_t ii = 0; ii < S_.cols(); ii++) {
const float radius = S_.col(ii).lpNorm<1>() - std::abs(S_(ii, ii));
const float eval_lo = S_(ii, ii) - radius;
constexpr float min_eval = 1e-3;
if (eval_lo < min_eval) S_(ii, ii) += radius + min_eval;
}
}
// Solve linear matrix equality S X = Y.
// NOTE: not 100% sure that this avoids dynamic memory allocation.
// 求解 X 的值
X_ = S_.householderQr().solve(Y_);
将 X 的值填充到 strategs 中
// Set strategy at current time step.
// 将求解出来的 P alpha 赋值给策略
for (PlayerIndex ii = 0; ii < dynamics_->NumPlayers(); ii++) {
strategies[ii].Ps[kk] = Ps_[ii];
strategies[ii].alphas[kk] = alphas_[ii];
}
更新 Z 和 ζ\zetaζ:

// Compute F and beta. 更新 Ft 和 β
F_ = lin.A;
beta_ = VectorXf::Zero(dynamics_->XDim());
for (PlayerIndex ii = 0; ii < dynamics_->NumPlayers(); ii++) {
F_ -= lin.Bs[ii] * Ps_[ii]; // F_t = A_t - \sum_{j=1}^N B_t^j P_t^j
beta_ -= lin.Bs[ii] * alphas_[ii]; // \beta_t = - \sum_{j=1}^N B_t^j \alpha_t^j
}
// Update Zs and zetas.
for (PlayerIndex ii = 0; ii < dynamics_->NumPlayers(); ii++) {
zetas_[kk][ii] =
(F_.transpose() * (zetas_[kk + 1][ii] + Zs_[kk + 1][ii] * beta_) +
quad[ii].state.grad)
.eval(); // \zeta &= q + F^\top (\zeta_{t+1} + Z_{ t+1} + \beta)
Zs_[kk][ii] =
(F_.transpose() * Zs_[kk + 1][ii] * F_ + quad[ii].state.hess).eval(); // Z &= Q + F_{}^\top Z F
for (const auto& Rij_entry : quad[ii].control) {
const PlayerIndex jj = Rij_entry.first;
const MatrixXf& Rij = Rij_entry.second.hess;
const VectorXf& rij = Rij_entry.second.grad;
zetas_[kk][ii] += Ps_[jj].transpose() * (Rij * alphas_[jj] - rij); // zeta 的剩余部分
Zs_[kk][ii] += Ps_[jj].transpose() * Rij * Ps_[jj]; // Z 的剩余部分
}
AL-iLQR
具体来说,该方法通过引入拉格朗日乘子,将约束条件整合到目标函数中,并通过逐步增加惩罚项来逼近或违反约束条件。
LA(x,λ)=f(x)+λ⊤c(x)+12c(x)⊤Iμc(x),s.t.c(x)=0.\begin{align*} \mathcal{L}_A(x, \lambda) &= f(x) + \lambda^\top c(x) + \frac{1}{2} c(x)^\top I_\mu c(x), \\ \text{s.t.} \quad & c(x) = 0. \end{align*}LA(x,λ)s.t.=f(x)+λ⊤c(x)+21c(x)⊤Iμc(x),c(x)=0.
求解器调用代码
求解器迭代调用
// 求解器迭代,如果求解器超过最大迭代次数或者超时则不再进入 while
while (num_iterations < params_.max_solver_iters && !has_converged &&
elapsed < max_runtime - timer_.RuntimeUpperBound()) {
// Start loop timer.
timer_.Tic();
将转移方程线性化:
// 如果 x_t=1 = f(x_t,u_t)不是线性的,将其线性化
if (!problem_->Dynamics()->TreatAsLinear())
ComputeLinearization(current_operating_point, &linearization_);
调用求解器:
// 调用刚才 iLQGame 求解器,得到策略
current_strategies = lq_solver_->Solve(
linearization_, cost_quadraticization_,
problem_->InitialState() - current_operating_point.xs.front(),
&delta_xs, &costates);
调整步长更新策略,防止 cost 越来越大,无法收敛:

if (!ModifyLQStrategies(delta_xs, costates, ¤t_strategies,
¤t_operating_point, &has_converged)) {
// Maybe emit warning if exiting early.
VLOG(1) << "Solver exited due to linesearch failure.";
// Handle success flag.
if (success) *success = false;
return log;
}
计算当前 cost :
// Compute total costs and check if we've converged.
// 计算这次迭代下的累计 cost
TotalCosts(current_operating_point, &total_costs);
1h37
相关数学
Hessian 矩阵
在 iLQR 目标函数公式中
c(xt,ut)=12[xtut]⊤Ct[xtut]+[xtut]⊤ctquadraticc(\mathbf{x}_t, \mathbf{u}_t) = \frac{1}{2} \begin{bmatrix} \mathbf{x}_t \\ \mathbf{u}_t \end{bmatrix}^\top
\mathbf{C}_t
\begin{bmatrix} \mathbf{x}_t \\ \mathbf{u}_t \end{bmatrix} + \begin{bmatrix} \mathbf{x}_t \\ \mathbf{u}_t \end{bmatrix}^\top \mathbf{c}_t
\quad \text{quadratic}c(xt,ut)=21[xtut]⊤Ct[xtut]+[xtut]⊤ctquadratic
其中 Ct 就是 Hessian 矩阵,当代价函数中存在如绝对值项,非线性项,iLQR 会按当前点做泰勒展开,泰勒展开里的“二次项系数矩阵”就是 Hession 矩阵
相关参考
- https://blog.youkuaiyun.com/qq_36497771/article/details/140370616






















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








