基于PD-NOMA的MEC资源分配

原创于 2025-10-11 00:22:32 发布 · 334 阅读

8 ·

CC 4.0 BY-SA版权

文章标签：

#PD-NOMA # 移动边缘计算 # 资源分配 # 优先级调度 # 多用户多任务

基于PD‐NOMA的移动边缘计算系统中的资源分配：多用户多任务优先级

1引言

1.1 研究现状

随着当今移动应用和移动技术的进步，移动设备（MDs）在我们的日常生活中发挥着至关重要的作用。由于移动设备的广泛应用及其应用程序的过度使用，例如交互式在线游戏、手势识别、人脸识别、语音控制和增强现实（AR），传统的无线蜂窝网络已无法满足用户所需的服务质量（QoS）。1为应对这一挑战，移动云计算（MCC）作为一种具备强大计算能力的新范式应运而生。由于云服务器的计算能力远高于移动用户的有限能力，将计算任务卸载到云服务器可以降低移动用户计算任务的延迟。2在基于MCC的网络中，由于用户与云之间的距离不同，可能会产生较大的延迟，而这对于某些服务而言是不可接受的。为解决此问题（长延迟），应将云服务迁移至用户附近，即移动网络的边缘。因此，移动边缘计算

https://doi.org/10.1002/ett.3631

本文档由 funstory.ai 的开源 PDF 翻译库 BabelDOC v0.5.10 (http://yadt.io) 翻译，本仓库正在积极的建设当中，欢迎 star 和关注。

2 共 20 页

佩马尔德和莫卡里

移动边缘计算（MEC）被引入，该技术能够在无线蜂窝网络边缘附近的无线电接入网络内提供云计算能力。3

随着先进移动设备（MD）的发展以及物联网的出现，计算任务的种类急剧增加。4这些不同的计算任务可能在优先级上有所不同。为了有效提升移动边缘计算（MEC）应用并获得最大收益，任务调度策略在此环境中起着重要作用。由于每个用户需为其所使用的资源付费，因此我们需要一个合适的任务调度器，根据任务的优先级来决策这些计算任务，以保证所需的服务质量（QoS）。任务调度的目标是在最小化每个用户的总任务执行时间的同时，最大化移动网络运营商（MNO）的利润。任务调度的主要优势在于实现高性能计算和最佳系统吞吐量。5目前计算系统中已存在多种调度算法，如先来先服务调度、轮转调度、最小‐最小、最大‐最小、最适任务调度算法以及优先级调度。6

在无线蜂窝网络中，多址接入技术可分为两种不同的方式，即正交多址接入（OMA）和非正交多址接入（NOMA）。7正交多址接入技术，例如正交频分多址接入（OFDMA）和时分多址接入（TDMA），已在无线蜂窝网络中广泛使用。8非正交多址接入技术，例如功率域非正交多址接入（PD‐NOMA），已成为第五代无线网络的一种新型多址接入技术。9该技术通过在发射机端采用叠加编码（SC）以及在接收机端采用连续干扰消除（SIC），可显著提高频谱效率。10

1.2 贡献

主要贡献可归纳如下。

研究了在功率域非正交多址接入辅助的多用户多任务场景中，联合分配上行/下行通信资源和计算资源以及任务调度所带来的优势。为此，提出了一种新的多用户、多任务、非抢占式优先级M/G/1排队模型，用于移动边缘计算系统中的计算任务。然后，建立了一个优化问题，在满足不同优先级计算任务的服务质量约束，以及各用户和基站的最大服务速率和功耗约束条件下，最大化总利润。

•在所提出的数学框架方面，设计了一种高效的传输感知与计算资源分配联合算法。在该方法中，上行链路/下行链路发射功率、子载波以及计算资源的分配由中央调度器统一进行。由于该优化问题属于混合整数非线性规划（MINLP），且具有非凸性和难解性，因此利用著名的交替搜索方法（ASM）将原问题分解为两个子问题：（1）联合功率与服务速率分配；（2）子载波分配。对于第一个子问题，我们采用连续凸逼近（SCA）方法结合双凹函数差近似方法（D.C. approximation method），将非凸问题近似转化为凸问题。为了求解作为整数规划问题的子载波分配子问题，我们应用了两种方法：（1）扩展盖尔‐沙普利算法，并提出一种新的匹配算法来解决子载波分配子问题；（2）对优化变量进行松弛，并结合DC逼近方法采用SCA方法求解。

在所提出的仿真结果中，将基于优先级的方案与无优先级方案的性能进行了比较。此外，评估了在上行链路和下行链路中使用功率域非正交多址接入技术相较于基于OMA的方案的性能增益。同时，我们还比较了所提出方案在子载波分配子问题中的优势。值得注意的是，穷举搜索方法与所提出的PD‐NOMA‐SCA中的优先级排队方案之间的性能差距约为7%。

1.3 论文组织结构

本文的其余部分组织如下。第2节讨论了相关工作。第3节介绍了提出的系统模型并给出了优化问题。第4节分析了资源分配问题和提出的算法。第5节研究了提出算法的计算复杂度。第6节给出了仿真结果与讨论。最后，第7节对本文进行了总结。

佩马尔德和莫卡里 20 中的 3

2 相关工作

近年来，移动边缘计算已从多个角度进行了研究。总体而言，移动边缘计算领域的研究分为两大类：（1）单任务和（2）多任务。下文将对其进行简要分析。

2.1 多接入边缘计算系统中的单任务

已有大量研究针对在MEC系统中计算相同计算任务的问题（例如，参见其他文献11‐19及其中的参考文献）。You等人11研究了基于TDMA和OFDMA的多用户MEC系统的资源分配问题，并将优化问题建模为最小化加权移动能量消耗总和。此外，Wang等人12研究了一种基于TDMA的多用户MEC系统，该系统具备在移动设备（MD）中收集能量的能力。作者提出了一种最优资源分配方案，通过联合优化接入点（AP）处的能量发射波束成形、中央处理单元（CPU）频率、用户端的卸载比特数以及用户间的时间分配，以最小化接入点（AP）的总能耗。Plachy等人13提出了一种算法，能够同时选择通信路径并进行虚拟机（VM）部署。此外，利用对用户移动的预测来应对系统的动态性。该方法用于动态虚拟机部署，并根据预期的用户移动找到最合适的通信路径。与此同时，Sardellitti等人14研究了一个多输入多输出多小区移动边缘计算系统，旨在最小化用户的总能耗。另外，Wang等人15考虑了在MEC服务器上具备内容缓存能力的MEC系统。他们将计算卸载决策、资源分配和内容缓存策略作为优化变量，并将最大化网络总收益作为优化问题的目标函数。此外，Kiani和Ansari16以及Wang等人17分别设计了采用二进制卸载情况和部分卸载情况的基于非正交多址的移动边缘计算系统，并通过计算与通信资源分配来最小化MEC用户的能耗。此外，Jeong等人18提出了针对无人机在频分双工模式下通过正交多址或非正交多址技术进行上行链路和下行链路通信及计算的联合比特分配方法。具体而言，他们通过采用连续凸逼近策略最小化总的移动能耗并求解该问题。Yu等人19提出了一种联合调度算法，用于分配无线资源和计算资源。具体而言，他们考虑了一个基于OFDMA的多用户系统中的云小站，研究了任务卸载时的子载波分配以及云小站中任务执行的CPU时间分配。

尽管其他作者11‐18提出了高效的计算和通信资源分配算法，但他们仅考虑了每个用户相同的计算任务。在实际中，每个用户存在多个具有不同优先级的计算任务。基于上述观察，似乎现有研究忽略了任务调度算法和排队延迟的影响。由于这些参数在移动边缘计算系统中对最大化移动网络运营商利润和最小化每个用户的总延迟具有重要作用，因此我们应在问题建模中考虑这些参数。

2.2 多接入边缘计算系统中的多任务

实际上，尽管存在各种具有不同优先级的待处理任务，但针对多任务移动边缘计算系统的研究仍然较少。最近，提出了一些关于单用户多任务移动边缘计算系统的工作。20,21丁等人20提出了一种优化框架，用于将单个移动设备上的多个计算任务卸载到多个具有计算能力的邻近接入点，旨在通过联合优化任务分配决策和移动设备的CPU频率，最小化所有任务的执行延迟以及移动设备的能量消耗。在丁等人的研究中，20假设接入点拥有完整的信道状态信息，因此移动设备已知上行链路和下行链路数据速率，而发射功率和子载波分配被忽略。

此外，毛等人21基于ASM，对具有多个独立任务的MEC系统的任务卸载调度和发射功率分配进行联合优化，旨在最小化执行时延和设备能耗的加权和。另外，在毛等人21的研究中，考虑了无线资源受限系统，每个时刻只能卸载一个任务，且MEC服务器按顺序执行不同的任务。他们还假设每个移动设备的计算资源非常有限，因此所有计算任务都应卸载到MEC服务器进行移动边缘执行。

20 中的 4

佩马尔德和莫卡里

除了多接入边缘计算系统外，针对移动云计算系统22和云环境5,23中的多任务调度场景，相关研究较少。陈等人22考虑了一种通用的多用户多任务移动云计算系统，旨在联合优化所有用户的任务卸载决策以及计算和通信资源的分配，以最小化所有用户的能耗、计算和时延总成本。此外，达克沙伊尼和古鲁普拉萨德5以及李23在云环境中研究了具有不同优先级的多任务算法。需要注意的是，上述针对云环境中基于优先级调度的研究仅通过启发式方法分配计算资源。值得注意的是，如何高效利用云计算资源是云计算服务提供商的主要目标之一。尽管如此，当我们将无线资源与计算资源进行联合分配时，相比独立分配的情况能够实现更高的性能。

3 系统模型

3.1 网络模型

考虑一个具有U个用户（表示为集合 ={1, 2,…,U}）的多用户多接入边缘计算系统，该系统配备一个集成MEC服务器的单天线基站。每个用户可同时请求多个任务。MEC服务器可在基站处执行计算任务和任务调度。图1显示了所考虑的网络模型。在此系统模型中，我们关注上行链路和下行链路。

示意图0

3.2 非抢占式优先级M/G/1排队模型

这里假设用户具有非常有限的计算资源，因此所有计算任务都应卸载到MEC服务器上执行。21此外，我们假设有不同类型的任务，任务类别的数量用KTot表示。另外，用户u的计算任务集合表示为u={1, 2, 3,…,Ju}，Ju ≤KTot表示用户u的计算任务数量。假设这些计算任务是具有不同优先级的独立任务，因此根据其不同的优先级被划分为KTot个不同的类别。

BS
User
MEC服务器
MEC服务器执行和排队
下行链路中的干扰
发射机
移动设备 u
MEC服务器
边缘计算
天线
u L bits

任务1			任务2
						任务J


Task
调度器

—	—	—	—	—	—	—	—	—






	非抢占式优先级M/G/1排队非抢占式优先级	非抢占式优先级M/G/1排队非抢占式优先级	非抢占式优先级M/G/1排队非抢占式优先级	非抢占式优先级M/G/1排队非抢占式优先级	非抢占式优先级M/G/1排队非抢占式优先级	非抢占式优先级M/G/1排队非抢占式优先级	非抢占式优先级M/G/1排队非抢占式优先级	非抢占式优先级M/G/1排队非抢占式优先级
	非抢占式优先级M/G/1排队非抢占式优先级	非抢占式优先级M/G/1排队非抢占式优先级	非抢占式优先级M/G/1排队非抢占式优先级	非抢占式优先级M/G/1排队非抢占式优先级	非抢占式优先级M/G/1排队非抢占式优先级	非抢占式优先级M/G/1排队非抢占式优先级	非抢占式优先级M/G/1排队非抢占式优先级	非抢占式优先级M/G/1排队非抢占式优先级

示意图1

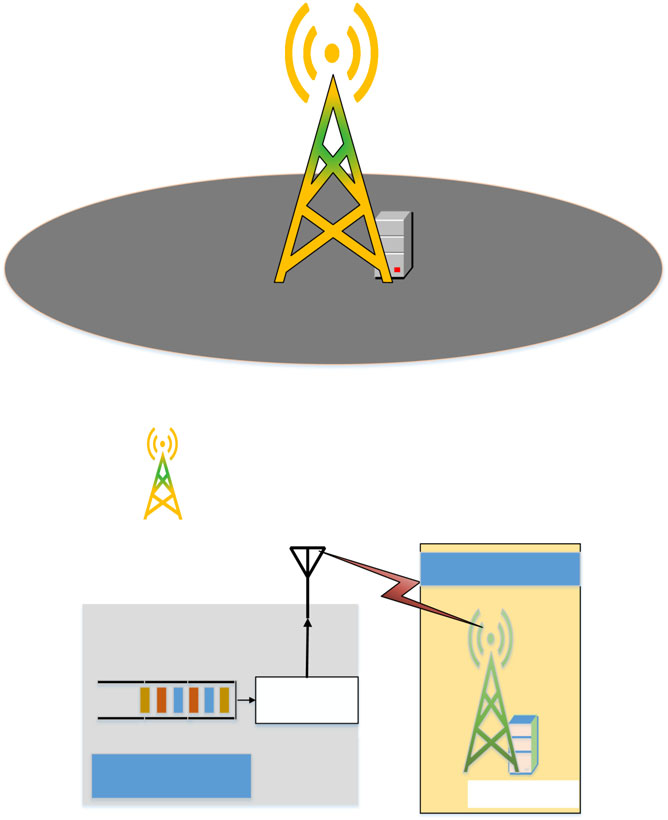
计算任务被卸载到MEC服务器。然后，任务调度器根据计算任务预定义的优先级进行操作。24首先执行具有更高优先级的任务，接着依次处理优先级最低的任务。k值越小，其类别优先级越高，即1类在队列中具有最高优先级。对于用户u请求的每个计算任务k，Lu,k（单位为比特）和 θtolerant u,k（单位为秒）分别为输入大小和执行截止时间。任务到达MEC服务器的过程由参数为λu,k的泊松分布建模。为了对MEC服务器上的队列进行建模，我们采用M/G/1建模方法，并考虑非抢占式系统。23所有卸载到MEC服务器的用户计算任务的总平均到达率用∑u∈∑k∈u λu,k表示。任务调度器为MEC服务器分配一定资源，以通用服务时间分布处理任务k，其均值由tu,k表示。23我们在MEC服务器上设置一个大容量缓冲区，用于存储尚未执行的已卸载计算任务。在每一类中，任务按照其到达顺序进行处理，即先进先出（FIFO）。图2展示了所考虑的任务调度策略。来自用户u的计算任务k的平均服务速率记为μu,k，它遵循每类的通用分布，具体获取方式如下25：

μu,k= 1
tu,k .
(1)

为了实现系统平衡，我们考虑用μmax表示的MEC服务器的最大服务速率。值得注意的是，只有当∑u ∈ ∑k ∈ u λu,k μ max < 1时，MEC任务调度系统才能工作。根据利特尔定律，用户u在类别k中的每个任务的等待时间为 ≥ 1 23

DWait u,k =
∑
u∈
∑
k∈u
λu,k
(μu,k −φ) ·(μu,k − ∑
u∈
k
∑
i=1 λu,i)
, (2)

其中 φ=∑u∈ ∑ k−1 i=1 λu ,i如果 k> 1，否则φ= 0。

备注 1（计算任务模型） 。
完整描述计算任务所有方面的模型十分复杂。在现有的移动边缘计算（MEC）文献中，常用的两种计算任务模型是二进制计算卸载和部分计算卸载。在第一种方法中，高度集成或相对简单的任务无法被分割，必须在移动设备（MD）上本地执行，或整体卸载至MEC服务器。实际上，二进制卸载更容易实现，适用于不可分割的简单任务。另一方面，部分卸载允许将每个任务划分为多个子任务，例如增强现实应用中的计算子任务。具体而言，每个任务可被划分为两部分，其中一部分可在本地执行，另一部分可卸载至MEC服务器进行边缘执行。17

如果每个计算任务的不同子任务之间存在依赖关系，则不能忽略现有的依赖关系。因此，子任务的执行顺序不能随意选择，因为某些子任务的输出是其他子任务的输入。需要注意的是，这种依赖关系使得卸载模型变得非常复杂和困难，这类模型称为任务调用图。26

6 页（共 20 页）

佩马尔德和莫卡里

3.3 传输模型

考虑多用户多任务MEC系统的联合上行和下行。设WDn和WUp分别为下行链路和上行链路无线接入信道的带宽。基站将可用带宽（WUp，WDn）划分为上行链路和下行链路的子载波集合，分别表示为Up={1, 2,…,NUp}和Dn={1, 2,…,NDn}，其中NUp和NDn分别表示上行链路和下行链路中的子载波数量。上行链路和下行链路中每个子载波的带宽相同，分别记为WUp s和WDn s 。值得注意的是，PD‐NOMA技术应用于上行链路和下行链路中。在本研究中，假设每个子载波在下行链路最多可分配给ψDn个用户，在上行链路最多可分配给ψUp个用户。不失一般性，令hnDnu和hnUpu分别为基站与用户u在子载波nDn和nUp上的信道功率增益。令ρnDnu为下行链路二进制子载波分配指示符，其定义如下：

ρnDn u={1, if subcarrier nDn is assigned to user u, 0, otherwise.

此外， ρnUpu表示上行链路二进制子载波分配指示符，其定义与下行链路类似。用户 u通过子载波 nUp向基站卸载计算任务的发射功率，以及基站通过子载波 nDn向用户 u发送已执行任务的发射功率分别用pnUpu和pnDnu表示。用户 u在子载波 nUp上的上行链路数据速率可表示为

rnUp u= WUp s log2(1+ ρ
nUp u hnUp INOMA,nUp u +(σnUp)2) , (3)

其中 INOMA,nUpu= ∑
i∈
,i≠u
ρ
nUp
i p nUp i h nUpu表示在子载波nUphnUpu 来自用户  ∖{u}，其中对于每个用户 i ∈  ∖{u}，满足关系 hnUpi> hnUpu。实际上，在执行串行干扰消除（SIC）后，若 hnUpi< hnUpu，则基站对每个用户 i ∈ ∖{u}的干扰信号进行解码并移除。此外，(σnUp)2 是在基站处通过子载波 nUp 接收到的来自其他小区的加性高斯白噪声（AWGN）和干扰信号功率。因此，用户 u 到基站的上行链路数据速率为 rUp u=∑nUp ∈Upr nUpu。类似地，基站通过子载波 nDn 向用户 u 发送的下行链路数据速率可表示为

rnDn u= WDn s log2(1+ ρ
nDn u hnDn INOMA,nDn u +(σ nDn
u) 2), (4) 其中 INOMA，nDnu = ∑
i ∈ 
，i ≠ u
ρ
nDn
i p nDn i h nDnu是用户 u在子载波 nDn上的接收到的小区内干扰，而 (σ nDnu )2hnDnu <
hnDni
是接收到的加性高斯白噪声功率以及来自其他小区在子载波 nDn上用户 u处的干扰信号功率。相应地，用户 u的数据速率可通过 ruDn= ∑nDn ∈Dn
rnDnu获得。将用户 u的u，L‐比特计算任务卸载的上行链路传输时延可表示为

DUp u,k = Lu,k rUp u ι Up u,k , (5)

其中 ι Up u，k表示用户u的上行链路数据速率中用于将计算任务 k ∈ u卸载到基站的比例。类似地，在该卸载方案中，向用户u发送已计算任务的下行链路传输时延可表述如下：

DDn u,k = αu,k Lu,k ruD nι Dn u,k , (6)

其中， ι Dn u,k表示用户u用于传输计算任务k ∈ u给用户u的下行链路数据速率的比例。此外，项αu,kLu,k是卸载任务Lu,k的输出大小，需要分发给

*在此模型中，我们假设存在一个加性高斯白噪声干扰源（IS）节点，在下行链路和上行链路中每个子载波上对基站和所有用户产生干扰。因此，上下行链路中其他小区的干扰均可由该IS建模。28

佩马尔德和莫卡里 20 中的 7

用户 u，其中 αu,k 是一个正实数值。αu,k 的值取决于计算任务的规格，例如，在压缩任务中，0< αu,k ≤ 1，即单比特计算任务被压缩为 αu,k 比特。20

3.4 总延迟和服务质量约束

假设任务计算采用非重叠方案，每个任务的总延迟是MEC服务器环境中的计算时间、排队延迟以及传输和接收持续时间的总和，其公式如下：

DTot u,k= DUp u,k+ D Wait u,k+ tu,k+ D Du,nk. (7)

假设 θtolerant u,k为执行截止时间。通常， θtolerant u,k是每个任务的最大容忍延迟。因此，为了满足任务计算的服务质量要求，应考虑以下约束：

DTot u,k ≤ θtolerant ,∀u ∈. (8)

3.5成本函数和问题建模

所考虑的移动网络运营商拥有无线与计算资源，拥有MEC服务器，并向用户提供MEC服务。该移动网络运营商的主要问题是如何联合分配计算和无线资源以最大化网络利润。我们假设γu,k和ηu,k分别为任务等待时间和MEC服务器中任务处理时间的成本单位。此外， βu为将计算任务传输到用户u的功耗成本单位。另一方面，传输和接收计算任务的收益单位分别由 ξUP u和 δu表示。因此，我们可以得到所考虑的移动网络运营商的总利润函数为

πProfit Tot=∑ u∈[(ξUP u rUp u+ δDn u ruDn)−(βu NDn
∑
nDn=1
pnDn u+ ∑
k∈u (γu,kD Wait u,k + ηu,ktu,k))]. (9)

在本文中，我们的目标是在满足每个计算任务的服务质量、传输功率限制、子载波分配约束和服务速率约束的前提下，最大化移动网络运营商的利润函数。为了简化符号表示，我们记p=[p nDnu ,p nUpu],ρ=[ρ nDnu ρ nUp
u]和 μ=[μu,k]。因此，该优化问题可表述如下： max
p,ρ,μ
πProfit Tot (10a) s.t.(8),
μu,k ≤ μ max ,∀u ∈, k ∈u, (10b)
∑
n U p ∈ U p
ρ n Up u p
n Up u ≤ Pmax ,∀u ∈, (10c)
∑
n Dn ∈ Dn
∑
u∈
ρ n Dn u p
n Dn u ≤ Pmax BS , (10d)
∑
u∈ 
ρ n U p u ≤ψ Up,∀nUp ∈Up , (10e)
∑
u ∈ 
ρ n Dn u ≤ψ Dn ,∀nDn ∈Dn, (10f)
ρ n U p
u , ρ n Dn u ∈{0, 1}, (10g)
p
n Dn
u ,p
n U p u ≥ 0, (10h)
20 中的 8

佩马尔德和莫卡里

其中，(10b) 表示基站为其分配给用户的任务所提供的服务速率，必须小于基站的最大服务速率容量。(10c) 和 (10d) 分别表示每个用户和基站的最大功率约束。在 (10c) 和 (10d) 中，Pmax u 和 Pmax BS 分别表示基站和用户 u 的最大发射功率。此外，(10e) 和 (10f) 为下行链路和上行链路中的独占子载波分配约束，其中每个子载波在小区内最多可分别分配给 ψDn 和 ψUp 个用户。

4 解决方案

优化问题(10)是一个包含连续变量和整数变量的混合整数非线性规划问题。目标函数(10a)是非凸的，此外，约束条件(8)也是非凸的。因此，优化问题(10)是非凸的，对于此类问题寻找全局最优解非常具有挑战性。在不失一般性的前提下，我们提出一种基于ASM、SCA和匹配方法的低复杂度且近似最优的算法来求解(10)。通过利用ASM，优化问题(10)被分解为两个子问题：(1) 寻找联合服务速率分配 μ和服务速率分配；以及(2) 寻找子载波分配 ρ。我们持续执行ASM，直到在期望的精度上不再有改进，或者迭代次数超过阈值。ASM的伪代码如算法1所示，其中S1为迭代次数阈值， ε1表示算法的精度。

4.1 寻找联合服务速率分配 μ和功率分配 p

在第一步中，我们找到联合服务速率分配 μ和功率分配p。因此，优化问题(10)表述如下：

max
p,μ
π Profit Tot (11)
s.t.(8),(10b)-(10d),(10h), 其中约束条件(8)为非凸形式，因为项DTot u,k包含分数和非线性函数。为此，我们首先应用上镜法 29并引入新的辅助变量 1 xu, k, yu,k 和 1 vu, k，分别作为DUp u,k、DWait u,k 和 DDn u,k 的上界值。 20由此，将(8)转换为以下约束条件：

1
xu,k + yu,k + 1
μu,k
+ 1
vu,k ≤ θ tolerant u,k .
(12)

优化问题(11)的目标函数也包含项DWait u,k，因此，目标函数被转化为等效形式：

π ′Profit Tot=∑
u ∈ [(ξ UP u rUp u+ δ Dn N Dn
∑
n Dn =1
p
n Dn u+ ∑
k ∈  u (γu, kyu , k+ ηu , ktu, k))]. (13)

佩马尔德和莫卡里 20 中的 9

因此，优化问题(11)被转化为以下问题： max
p,μ,x,y,v,
π′Profit Tot (14a)
s.t. Lu,kxu,k ≤ ruU pιUu,pk, (14b) αu,kLu,kvu,k ≤ ruD nιDu,nk, (14c)
ln(yu,k)+ ln(μu,k −φ)+ ln(μu,k −∑ u∈
k ∑i=1 λu,i) ≤ ln(∑ u∈∑ k∈ λu,k) (14d)
(10b)-(10d),(12).

由于上行链路和下行链路数据速率关于p是非凹的，因此(14b)和(14c)为非凸约束。因此，优化问题(14)仍然是非凸的。为此，我们利用SCA算法基于DC逼近方法将rUp u和ruDn近似为凹形式。8所提出的结合DC逼近方法的SCA算法总结于算法2中。

因此，我们首先将上行链路和下行链路的接入数据速率分别表示为以下微分形式：

rnUp u= f nUp
u − g
nUp
u (15)
and
rnDn u= f nDn
u − g
nDn
u, (16) 其中，凹函数 f nUpu、f nDnu、g nUp
u 和 g nDnu 分别由下式给出：

f
nUp u= WUp s log2(ρ nUp
u p
nUp u+ INOMA,nUp +(σ nUp) 2), (17)
f n Dn s log2(ρ n Dn u p
n Dn Dn +(σ n Dn u) 2), (18)
g
n p s log2(I NOMA,nUp
u +(σ n U p) 2), (19)
and
g
n Dn s log2(I NOMA,nDn
u +(σ n Dn u) 2). (20)

然后，在SCA的每次迭代s2中，我们分别对 g n U p u(p
n U p s 2 )和g
n Dn u(p
n Dn s 2 )进行近似
g
n U p u(p
n U p
s 2)≈ g n U p u(p n U p
s 2 − 1) + ∇g n U p
T n U p
s 2 − 1)(p n U p
s 2 −p
n U p
s 2 − 1) (21)
and
g
n Dn u(p
n Dn
s 2)≈ g
n Dn u(p n Dn
s 2 − 1) + ∇g n Dn T u(p n Dn
s 2 − 1)(p n Dn
s 2 −p
n Dn
s 2 − 1) , (22)
20 中的 10
佩马尔德和莫卡里

其中pnUp s2−1和pnDn s2−1由前一次迭代s2 −1 ≥ 0获得，ΔgnUpT u(pnUp s2−1)和ΔgnDnT u(pnDn s2−1)分别如公式(23)和(24)所示。

∇gnUpT u (pnUp) ⎧⎪⎨⎪⎩ WUp s ρni UphnUp u
(ln2)(I NOMA,nUp u +(σnUp)2)
, ∀i≠ u, hnUp u< hni,kUp, 0, otherwise.
(23)
∇gnDnT u (pnDn)= ⎧⎪⎨⎪⎩ WDn s ρni DnhnDn u (ln2)(INOMA ,nDn u +(σnDn u)2)
, ∀i≠ u, hnDn u< hni,Dn, 0, otherwise, (24)

根据上述内容，我们有

r̂nUp u(pnUp s2)≈ f nUp u(pnUp s2)− g nUp s2−1) −∇Tg nUp s2−1)(pnUp s2 −pnUp s2−1) , (25)
and
r̂nDn u(pnDn s2)≈ f nDn u(pnDn s2)− gnDn u(pnDn s2−1) −∇TgnDn u(pnDn s2−1)(pnDn s2 −pnDn s2−1) , (26)

其中，(25) 和 (26) 的右侧分别是 p Up s2 和 pnDns2, 的凹函数。在优化问题(14)中，接入数据速率̂rUpu= ∑nUp∈Up ̂
rnUpu(pnUps2) 和 ̂ruDn= ∑nDn∈Dn ̂rnDnu(pnDns2) 分别被替换为 rUpu 和 ruD n。由此，优化问题(14) 被近似为一个凸问题，可通过使用 CVX 优化软件求解。30
n

4.2 寻找子载波分配 ρ

为了解决作为整数问题的子载波分配问题，我们采用了两种方法：（1）我们开发了盖尔‐沙普利算法的扩展版本，并提出了一种新的匹配算法来解决子载波分配子问题；（2）我们对优化变量进行松弛，并结合DC逼近方法使用 SCA方法。以下我们将介绍上述方法。

4.2.1 通过匹配理论寻找子载波分配 ρ

我们采用匹配理论，因其具有高性能和低复杂度。31在此，我们利用匹配理论来解决子载波分配问题。因此，优化问题建模如下： max
ρ
πProfit Tot (27) s.t.(8),(10c)-(10g).

优化问题(27)是非凸的。由于(27)包含二进制变量 ρ，因此可将其建模为匹配问题。 32在通过求解优化问题(11)获得功率分配后，我们可以将(27)表述为多对多双边匹配问题，该问题可通过利用匹配理论来解决。为了更好地理解该匹配问题，下面我们简要解释它。此处，我们仅考虑下行链路中的子载波分配。我们将和Dn视为两个不相交的集合，它们希望相互匹配，以最大化各自的利益。如果子载波nDn被分配给用户u，则它们构成匹配对。我们假设每个参与者对另一集合中的参与者都有偏好，并将用户和子载波的偏好列表集表示为

χ={χ u(nDn),∀u ∈,χn Dn (u),∀nDn ∈Dn}, (28) 其中 χ u(nDn) 和 χn Dn (u) 分别是用户 u 和子载波 nDn 的偏好列表。我们假设每个子载波最多分配给小区用户中的
ψ Dn 个用户，其对不同用户的偏好表示为
Υ ≻
n Dn
Υ′ ,Υ ⊆,Υ ′ ⊆ ⇔ rnDn u(Υ)> rnDn u(Υ ′ ), (29) 其中≻是nDn上的一个完整且可传递的偏好关系，(29)表示nDn更偏好于 Υ中的用户而非 Υ′ nDn中的用户，因为前一组提供的收益高于后一组。注意，每个用户可以使用一个或多个子载波。这些子载波上的偏好关系可以表示为
nDn ≻u n′ Dn ⇔ hn Dn
u > h n ′ Dn
u , (30)
佩马尔德和莫卡里 20 中的 11

其中，(30) 表示用户 u 比较偏好子载波 nDn 而非子载波 n′ Dn ，因为子载波 nDn 提供的信道功率增益高于子载波
n′ Dn。因此，为了解决所提出的基于 PD‐NOMA的系统的用户与子载波匹配问题，我们开发了盖尔‐沙普利算法 33
的一个扩展版本，并提出了一种新的匹配算法。在所提出的算法中，当每个用户与其匹配的子载波配对时，它会向该子载波发起提议。每个子载波有权根据优化问题(27)和(30)的约束条件来接受或拒绝这些提议。我们利用所提出的匹配算法来求解优化问题(27)。该算法包括两个步骤，即初始化和匹配过程。在初始化步骤中，每个用户根据 (30)选择其偏好列表。因此，创建 {SCmatch} 列表以记录被分配到优先子载波的用户。在匹配过程中，每个用户向其最偏好的子载波 χ u(nDn) 发起提议，然后我们检查子载波nDn 对应的优化问题(27)的约束条件。如果该提议满足优化问题(27)的约束条件，则将其添加到 {SCmatch} 列表中。当没有用户愿意再提出新的提议时，匹配过程终止。
所提出的匹配算法在算法3中进行了描述。

4.2.2 通过松弛方法寻找子载波分配 ρ via relaxationmethod

约束(10h)为二进制形式。我们需要将二进制变量 ρ松弛为实值变量，即 0 ≤ ρ nUpu ≤ 1和0 ≤ ρ nUp
u≤ 1。34该松弛
变量可解释为U用户利用子载波 ρ nUpu或ρ nDnu的时隙共享因子。因此，为了求解 ρ，类似于前一小节，通过使用上镜法，我们求解以下等效优化问题：
max
ρ,x,y,v
π ′Profit Tot (31a)
s.t. 0 ≤ ρ n Up u ≤ 1, (31b)
0 ≤ ρ n Dn u ≤ 1, (31c)
(10c)-(10f),(12),(14b)-(14d).

类似于(15)和(16)，我们首先将下行链路和上行链路数据速率表示为DC形式，并分别对g
n U p u(ρ
n U p
s 2 )和g
n Dn u(ρ
n Dn
s 2 )进行近似。
g
n U p u(ρ n U p
s 2)≈ g n U p u(ρ n U p
s 2 − 1) + ∇g n U p
T u(ρ n U p
s 2 − 1)(ρ n U p
s 2
−ρ
n U p
s 2 − 1) (32)
and
g
n Dn u(ρ
n Dn
s 2)≈ g
n Dn u(ρ n Dn
s 2 − 1) + ∇g n Dn T u(ρ n Dn
s 2 − 1)(ρ n Dn
s 2
− ρ
n Dn
s 2 − 1) , (33)
12 of 20 PAYMARD AND MOKARI

其中 ρnUp s2−1和 ρnDn s2−1由前一次迭代s2 − 1 ≥ 0获得，使得∇gnUpT u(ρnUp s2−1)和∇gnDnT u(ρnDn s2−1)分别表示为 (34)和(35)。

∇gnUpT u (ρnUp)= ⎧⎪⎨⎪⎩ WUp s pni UphnUp u
(ln2)(I NOMA,nUp u +(σnUp)2)
, ∀i≠ u, hnUp u< hniUp ,
0, otherwise.
(34)
∇gnDnT u (ρnDn)= ⎧⎪⎨⎪⎩ WDn s pnDn i hnDn u (ln2)(INOMA ,nDn u +(σnDn u )2)
, ∀i≠ u, hnDn u< hniDn ,
0, otherwise, (35)

因此，我们有
r̂nUp u(ρ nUp u(ρ nUp s2)− g nUp u(ρ nUp s2−1) −∇g
nUpT u(ρ nUp s2−1)(ρ nUp
s2 −ρ
nUp s2−1) , (36)
and
r̂nDn u(ρ
nDn
u(ρ
nDn u(ρ nDn s2−1) −∇gnDnT u(ρ nDn s2−1)(ρ nDn
s2 −ρ
nDn s2−1) , (37)
其中(36)和(37)的右侧分别是 ρ nUp s2和ρ nDns2,的凹函数。随后，在优化问题(31)中， ̂rUp u=∑nUp∈Up ̂rnUpu(ρ nUp s 2)和 ̂ruDn = ∑nDn∈Dn ̂rnDnu(ρ nDns2)分别被替换为rUp u和ruD n。通过此替换，优化问题(31)是凸的，可以通过 CVX求解器求解。

命题1. 在提出的算法1中，目标函数在每次迭代s1后要么得到改进，要么保持不变。它有下界零，因此算法1收敛到一个局部最优解。

证明. 请参见附录。

5 计算复杂度

本节将讨论ASM和所提出的匹配算法所需的计算复杂度。算法1的计算复杂度随着约束条件数量和优化变量数量呈指数增长。由于ASM中的计算复杂度与迭代次数呈线性关系，而迭代次数又取决于算法的精度。此处的目标是获得算法1在一次迭代中的计算复杂度。算法1包含两层迭代。在第一层迭代中，我们使用SCA算法获得优化变量p和μ。
在每次迭代中，通过CVX求解器求解(10)的近似凸问题。值得注意的是，CVX软件基于内点法（IPM）。因此，根据Mokari等人的研究，35求解(14)的计算复杂度为(log((Υ)∕t0ρ) log(ξ))，其中 Υ=(10+ K)U+ 1是(14)中的总约束数，t0是用于逼近IPM精度的初始点， 0< ρ ≪ 1是IPM的停止准则， ξ用于更新IPM的精度。在第二层迭代中，我们求解 ρ。我们提出了两种方法来解决子载波分配问题。首先，我们获得SCA的计算复杂度，然后计算所提出的匹配算法的计算复杂度。我们对优化变量ρ进行松弛，并采用DC逼近方法的SCA方法，最后通过CVX求解。因此，在SCA的每次迭代中求解(31)的计算复杂度为(log((Ω)∕t0ρ) log(ξ))，其中 π= 10U+ NUp+ NDn+ 1是(31)中的总约束数。需要注意的是，迭代式SCA算法的总计算复杂度取决于SCA迭代的次数。接下来我们给出所提出的匹配算法的计算复杂度。在上行链路中，所提出的匹配算法用于配对子载波和用户的计算复杂度为(U × NUp ×M)， 32其中M是(27)中上行链路约束的总数。此外，在下行链路中，所提出的匹配算法用于配对子载波和用户的计算复杂度定义方式与上行链路类似。因此，所提出的匹配算法的总计算复杂度为((U ×NUp ×M)+(U ×NDn ×S))，其中S是 (27)中下行链路约束的总数。穷举搜索的计算复杂度如下所示。在所考虑的系统中，若假设优化变量p和 μ分别有
Kpos和Epos个不同的可能取值，则需要进行((2Kpos) (U ×N Dn +U×NU p ) ×(Epos) U×K )次不同的搜索才能找到最优解。注意
佩马尔德和莫卡里 20 中的 13

表1 不同求解方法的复杂度阶数
方法复杂度阶数
穷举搜索 (2Kpos)(U×NDn+U×NUp) ×(Epos)U×K
功率分配：SCA‐DC log((Υ)∕t0ρ) log(ξ)
子载波分配：SCA‐DC log((Ω)∕t0ρ) log(ξ)
子载波分配：匹配 (U ×NUp ×M)+(U ×NDn ×S)
优化变量 ρ取2个值（ρnUpu ρnDnu∈{0, 1}）。ASM和所提出的匹配算法的计算复杂度在表1中进行了总结。

6 仿真结果

在本节中，我们给出了数值结果以验证我们的分析并评估所提出的算法1的性能。在仿真中，我们假设八个用户在 290至300米范围内服从均匀分布。我们对接入信道采用瑞利信道衰落模型。因此，信道功率增益呈均值为0.5的指数分布。信道功率增益的路径损耗模型的路径损耗指数假设为2，这与城区蜂窝无线电相兼容。此外，我们设置 WDn= 1 MHz，WUp= 1 MHz，NDn= 16，NUp= 16。加性高斯白噪声功率(σnDnu )2和(σnUp)2设为 10−11W。
假设基站的最大服务速率设置为μmax= 500 1秒。输入任务大小设为 104比特，任务执行截止时间对应于计算任务的优先级。任务以一定的速率λu,k按照泊松分布到达MEC服务器。我们假设K = 3，且1类、第二类和第三类的执
行截止时间分别设为100毫秒、300毫秒和600毫秒。我们假设 βu= 200, ξUP u= 10−6和 δu= 10−6。同时考虑γu,k和
ηu,k分别对1类、第二类和第三类设为100、20和1。每个用户u和基站的最大允许发射功耗分别设为Pmax u= 50 m W和Pmax BS = 15W。我们假设在下行链路和上行链路中，每个子载波最多可分配给小区内的两个用户，即 ψDL= ψUp= 2。数值结果中的仿真参数在表2中给出。

这里，我们比较以下方案。

• OMA-匹配中的优先级队列：用户的计算任务根据其优先级被卸载到基站并进行调度。该方案对应于通过设置 ψ
Up= ψDn= 1来求解优化问题(10)。在此方案中，我们考虑在上行链路和下行链路均采用OFDMA技术。此外，我们利用匹配算法来解决子载波分配问题。

表2 系统参数
参数值
用户数量 U= 8 基站覆盖半径 300米加性高斯白噪声功率 (σ n Up) 2=(σ n Dn u ) 2= 10− 11 W
信道功率增益分布的均值 0.5 路径损耗指数 2 下行链路带宽 WDn= 1MHz
上行链路带宽 W U p = 1MHz
上行子载波数量 NUp = 16
下行子载波数量 NDn= 16 基站最大发射功率 Pmax BS
= 15W
每个用户最大发射功率 Pmax u = 50毫瓦 MEC服务器的最大服务速率 μ max= 500
输出任务大小与输入任务大小之比 α u= 0.2
缩写：AWGN，加性高斯白噪声；BS，基站；MEC，移动边缘计算。
20中的14 佩马尔德和莫卡里

• OMA-匹配中的无优先级排队：用户的计算任务被卸载到基站并以无优先级方式调度（基于先进先出）。换句话说，所有计算任务具有相同的优先级。因此，根据利特尔定律，每个任务的等待时间如下所示25：
DWait u,k= ∑u∈∑k∈uλu,k
μu,k(μu,k −∑u∈ ∑ ki=1 λu,k)
. (38)
该方案对应于通过设置 ψUp= ψDn= 1并用(38)替换(2)来求解优化问题(10)。在此方案中，我们对上行链路和下行链路均采用OFDMA技术。此外，我们利用匹配算法来解决子载波分配。

• OMA-SCA中的优先级队列：用户的计算任务被卸载到基站，并根据其优先级进行调度。该方案对应于通过设置 ψ
Up= ψDn= 1 来求解优化问题(10)。在此方案中，我们对上行链路和下行链路均采用OFDMA技术。此外，我们利用SCA方法结合DC逼近方法来解决子载波分配。

• OMA-SCA中的无优先级排队：用户的计算任务被卸载到基站，且无优先级地进行调度。换句话说，计算任务具有相同的优先级。该方案对应于通过设置 ψUp= ψDn= 1 并用(38)替换(2)来求解优化问题(10)。在此方案中，我们对上行链路和下行链路均采用OFDMA技术。此外，我们应用SCA方法结合DC逼近方法来解决子载波分配。

•PD-NOMA匹配中的优先级排队：用户的计算任务被卸载到基站，并根据其优先级进行调度。该方案对应于通过应用匹配算法求解子载波分配来解决优化问题(10)。在此方案中，我们考虑在上行链路和下行链路中均采用PD‐NOMA技术。

• PD-NOMA-匹配中的无优先级队列：用户的计算任务被卸载到基站，且不按优先级进行调度。该方案对应于通过用(38)替换(2)并应用匹配算法求解子载波分配来解决优化问题(10)。在此方案中，我们考虑在上行链路和下行链路中均采用PD‐NOMA技术。

• PD-NOMA-SCA中的优先级排队：用户的计算任务被卸载到基站，并根据其优先级进行调度。该方案对应于通过应用SCA方法结合DC逼近方法求解子载波分配问题来解决优化问题(10)。在此方案中，我们考虑在上行链路和下行链路中均采用PD‐NOMA技术。

• PD-NOMA-SCA中的无优先级队列：用户的计算任务被卸载到基站，并且在没有优先级的情况下进行调度。该方案对应于通过用(38)替换(2)并应用基于DC逼近方法的SCA方法求解子载波分配，来求解优化问题(10)。在此方案中，我们考虑在上行链路和下行链路中均采用PD‐NOMA技术。

在图3中，我们展示了所考虑的方案下，提出的算法1的收敛性随迭代次数的变化情况。如图所示，通过应用匹配算法，所提算法1在3次迭代后收敛到某一固定值；而使用基于DC逼近方法的SCA方法时，在5次迭代后收敛。该结果表明，所提方法可在MEC网络中实际部署实施。

示意图2

图4描绘了不同方案下移动网络运营商（MNO）的总利润随最大发射功率的变化情况。在图4A和图4B中，我们分别研究了基站和用户发射功率限制对MNO总利润的影响。显然，随着基站和用户的最大发射功率增加，下行链路和上行链路的接入数据速率分别提高。因此，所考虑方案中MNO的利润也随之增加（通过提高接入数据速率）。
此外，如图4所示，PD-NOMA-SCA中的优先级排队和PD-NOMA匹配中的优先级排队方案相比OMA-SCA中的无优
先级排队和OMA-匹配中的无优先级排队方案为MNO带来了更高的利润。例如，如图4A所示，当Pmax BS= 18W时， PD-NOMA-SCA中的优先级排队方案中MNO的总利润相较于OMA-SCA中的优先级队列方案提高了约49%；而在图
4B中，当Pmax u= 60mW时，PD-NOMA-SCA中的优先级排队方案中MNO的总利润相较于OMA-SCA中的无优先级排队方案提高了约49%。其中性能最优的是PD-NOMA-SCA中的优先级排队，而相比之下性能最差的是OMA-匹配中
的无优先级排队方案。

图5研究了MEC服务器的最大服务速率对MNO总利润的影响。如图所示，在所有方案中，增加MEC服务器的最大服务速率会提高MNO的总利润。特别是，在Priority
佩马尔德和莫卡里 20 中的 15

500 600 700 800 900 1000 1100 1200 1300 1400 1500
MEC服务器的最大服务速率（sec-1）
-10
0
10
20
30
40
50
60
70
To tal pr ofi t o f M NO
PD‐NOMA‐SCA中的优先级排队 PD‐NOMA‐SCA中的无优先级队列 PD‐NOMA匹配中的优先级排队 PD‐NOMA‐匹配中的无优先级队列 OMA‐SCA中的优先级队列 OMA‐SCA中的无优先级排队 OMA‐匹配中的优先级队列 OMA‐匹配中的无优先级排队

2 2.5 3 3.5 4 4.5 5 5.5 6
最大带宽（MHz）
0
50
100
150
200
250
300
To ta l p ro fit o f M N O
PD‐NOMA‐SCA中的优先级排队 PD‐NOMA‐SCA中的无优先级队列 PD‐NOMA匹配中的优先级排队 PD‐NOMA‐匹配中的无优先级队列 OMA‐SCA中的优先级队列 OMA‐SCA中的无优先级排队 OMA‐匹配中的优先级队列 OMA‐匹配中的无优先级排队

PD-NOMA-SCA中的排队，这一点更为明显。此外，在所考虑的方案中，PD‐NOMA技术相比OMA具有更大的优势。另外，如图5所示，当 μmax= 1000时，PD-NOMA-SCA中的优先级队列方案与OMA-SCA中的优先级队列方案之间的性能差距接近43%。可以看出，随着MEC服务器最大服务速率的增加，基于优先级和非优先级的排队方案逐渐接近，实际上，这些方案中的处理和排队延迟大致相等。

在图6中，我们研究了不同方案下MNO的总利润随最大可用带宽的变化情况。注意，在该图中，总带宽被视为上行链路和下行链路带宽之和，且两者被均等分配。如图所示，当WUp和WDn取值较小时，不同方案之间的利润差
距非常小。随着上行链路和下行链路带宽的增加，MNO的总利润也随之增加。可以看出，PD-NOMA-SCA中的优
先级排队和PD-NOMA匹配中的优先级排队相比其他方案显著提升了性能增益（MNO的总利润）。此外，我们看到基于PD‐NOMA的方案相较于基于OMA的方案改善了MNO的性能增益（MNO的总利润）。从上述方案中可以看出，OMA-匹配中的优先级队列和OMA-匹配中的无优先级排队的表现最差。另外，如图6所示，不同方案之间的性能差距也被进行了比较。

图7绘制了移动网络运营商（MNO）的总利润随MEC服务器总到达率的变化情况。正如预期，随着任务总到达率的增加，等待时间也随之增加，因此MNO的总利润也相应减少。另一方面，由于计算和无线资源的容量是固定的，而总任务到达率增加，导致等待
佩马尔德和莫卡里 20 中的 17

18 36 54 72 90 0
50
100
150
To tal pr ofi t o f M NO
| |||||||||||||
| —|—|—|—|—|—|—|—|—|—|—|—|—|
| |||||||||||||
| |||||||||||||
| |||||||||||||
| |PD‐NOMA PD‐NOMA|PD‐NOMA PD‐NOMA|PD‐NOMA PD‐NOMA|PD‐NOMA PD‐NOMA|PD‐NOMA PD‐NOMA|‐SCA中的优先级排|‐SCA中的优先级排||||||
| |PD‐NOMA PD‐NOMA|PD‐NOMA PD‐NOMA|PD‐NOMA PD‐NOMA|PD‐NOMA PD‐NOMA|PD‐NOMA PD‐NOMA|‐SCA中的优先级排|‐SCA中的优先级排||||||
| |PD‐NOMA PD‐NOMA|PD‐NOMA PD‐NOMA|PD‐NOMA PD‐NOMA|PD‐NOMA PD‐NOMA|PD‐NOMA PD‐NOMA|‐SCA中的优先级排|‐SCA中的优先级排||||||
| |PD‐NOMA PD‐NOMA|PD‐NOMA PD‐NOMA|PD‐NOMA PD‐NOMA|PD‐NOMA PD‐NOMA|PD‐NOMA PD‐NOMA|‐SCA中的无优先级|‐SCA中的无优先级|‐SCA中的无优先级|队列|队列|||
| |PD‐NOMA PD‐NOMA|PD‐NOMA PD‐NOMA|PD‐NOMA PD‐NOMA|PD‐NOMA PD‐NOMA|PD‐NOMA PD‐NOMA|‐SCA中的无优先级|‐SCA中的无优先级|‐SCA中的无优先级|队列|队列|||
| ||||||PD‐NOMA匹配中的优先级排队 ‐匹配中的无优先级 OMA‐SCA中的优先级队列 OMA‐SCA中的无优先级排队 OMA‐匹配中的优先级队列
中的无优先级排队|PD‐NOMA匹配中的优先级排队 ‐匹配中的无优先级 OMA‐SCA中的优先级队列 OMA‐SCA中的无优先级排队 OMA‐匹配中的优先级队列
中的无优先级排队|PD‐NOMA匹配中的优先级排队 ‐匹配中的无优先级 OMA‐SCA中的优先级队列 OMA‐SCA中的无优先级排队 OMA‐匹配中的优先级队列
中的无优先级排队|队列|队列|||
| |||||PD‐NOMA|PD‐NOMA匹配中的优先级排队 ‐匹配中的无优先级 OMA‐SCA中的优先级队列 OMA‐SCA中的无优先级排队 OMA‐匹配中的优先级队列
中的无优先级排队|PD‐NOMA匹配中的优先级排队 ‐匹配中的无优先级 OMA‐SCA中的优先级队列 OMA‐SCA中的无优先级排队 OMA‐匹配中的优先级队列
中的无优先级排队|PD‐NOMA匹配中的优先级排队 ‐匹配中的无优先级 OMA‐SCA中的优先级队列 OMA‐SCA中的无优先级排队 OMA‐匹配中的优先级队列
中的无优先级排队|队列|队列|||
| |||||PD‐NOMA|PD‐NOMA匹配中的优先级排队 ‐匹配中的无优先级 OMA‐SCA中的优先级队列 OMA‐SCA中的无优先级排队 OMA‐匹配中的优先级队列
中的无优先级排队|PD‐NOMA匹配中的优先级排队 ‐匹配中的无优先级 OMA‐SCA中的优先级队列 OMA‐SCA中的无优先级排队 OMA‐匹配中的优先级队列
中的无优先级排队|PD‐NOMA匹配中的优先级排队 ‐匹配中的无优先级 OMA‐SCA中的优先级队列 OMA‐SCA中的无优先级排队 OMA‐匹配中的优先级队列
中的无优先级排队|队列|队列|||
| |||OMA‐匹配|OMA‐匹配|OMA‐匹配|PD‐NOMA匹配中的优先级排队 ‐匹配中的无优先级 OMA‐SCA中的优先级队列 OMA‐SCA中的无优先级排队 OMA‐匹配中的优先级队列
中的无优先级排队|PD‐NOMA匹配中的优先级排队 ‐匹配中的无优先级 OMA‐SCA中的优先级队列 OMA‐SCA中的无优先级排队 OMA‐匹配中的优先级队列
中的无优先级排队|PD‐NOMA匹配中的优先级排队 ‐匹配中的无优先级 OMA‐SCA中的优先级队列 OMA‐SCA中的无优先级排队 OMA‐匹配中的优先级队列
中的无优先级排队|队列|队列|||
| |||OMA‐匹配|OMA‐匹配|OMA‐匹配||||||||

1 2 3 4 5
基站最大发射功率（瓦特）
5
10
15
20
25
30
35
To ta l p ro fit o f M N O
基于优先级的功率域非正交多址穷尽搜索 PD‐NOMA‐SCA中的优先级排队 PD‐NOMA匹配中的优先级排队

对于低优先级类，时延增加。因此，为了满足优化问题(10)的约束，计算资源被分配给优先级较低的任务。因此，在计算任务到达率较高时，优先级方案与非优先级方案彼此趋于接近。

我们研究了在图8中的PD-NOMA-SCA中的优先级排队和PD-NOMA匹配中的优先级排队方案中，最优解（通过穷举搜索获得）与提出的算法1之间的性能差距。该图显示了移动网络运营商的总利润随最大发射功率的变化情况，对应于NUp= 4、NDn= 4和U= 2。如图所示，穷举搜索与PD-NOMA-SCA中的优先级排队方案之间的性能差距约为7%。此外，穷举搜索与PD-NOMA匹配中的优先级排队之间的性能差距约为15%，这意味着所提出的算法1相较于穷举搜索方法具有相当低的计算复杂度，是一个良好的解决方案。