基于贝叶斯的弯道车道估计

最新推荐文章于 2025-11-25 14:32:13 发布

原创最新推荐文章于 2025-11-25 14:32:13 发布 · 296 阅读

7 ·

CC 4.0 BY-SA版权

文章标签：

#自动驾驶 # 贝叶斯框架 # 多双曲线 # 道路标线 # 弯道检测

基于贝叶斯的自动驾驶弯道车道估计

摘要

过去十年中，许多关于智能感知的研究都致力于开发使车辆能够在复杂环境中高效行驶的算法。大多数现有方法要么处理时间无法满足实时性要求，要么在真实复杂环境中效率低下，同样无法满足此类关键功能的完全可用性约束。为了改进现有方案，本文提出一种基于贝叶斯框架估计多双曲线参数的弯道车道检测算法，以在具有挑战性的条件下实现弯道车道检测。其基本思想是将捕获的图像划分为多个部分，在每一部分上使用双曲线建模轨迹，并利用所提出的分层贝叶斯模型估计其参数。与现有技术中的研究成果相比，实验结果证明我们的方法在道路标线检测方面更高效且更精确。

关键词 自动驾驶 · 嵌入式摄像头 · 道路标线 · 多双曲线 · 贝叶斯框架

1 引言

自动驾驶是人工智能逐步演进的主要关注领域之一。事实上，通过识别和区分道路上的不同物体，并实时做出适当而准确的决策，以确保自动驾驶汽车机制的正常运行至关重要。

在这方面，为了提高道路安全，已开展多项关于自动驾驶的研究。智能车辆系统获取方法完全基于人工智能，通过尝试复制人类智能，更确切地说是机器学习/深度学习方法。智能汽车研发的主要目标是降低事故率，并通过检测不同的危险情况来提高交通使用的效率。

关于数据，现有技术研究通常依赖于自动驾驶汽车上的嵌入式设备，例如摄像头[单目（Nguyen等，2015年）、立体（Song等，2018年）或多摄像头（Ieng等，2005年）]或其他传感器，如里程计（Santana等，2013年）、惯性测量单元（Anwary等，2018年）、差分GPS（Chengping等，2014年或Kim和Park2017b）。嵌入式处理器可用于运行算法，以成功地从起点行驶到预定义目的地。执行该任务的主要困难通常在于可能存在其他车辆和障碍物（Zhou和Dong，2017年），以及交通标志的识别（Botekar和Mahalakshmi，2017年）。一些研究工作专注于通过基于三步算法的方法进行交通标志的检测与分类：颜色分割、形状识别和神经网络（Broggi等，2007年；Kim，2019年）。近年来，深度学习方法结合空间变换器和随机优化方法得到了研究（Arcos‐García等，2018年）。Saxena等（2015年）进行了一项有趣的调查研究。

在所有的自动驾驶功能中，自动驾驶汽车的横向定位仍然是需要认真解决的最重要任务之一。横向定位可以通过使用“同步定位与建图”方法来实现，这种方法允许一个全局定位过程。这类方法存在一些与问题表述相关的内在局限：无论SLAM方法使用的传感器是什么（Bresson等，2017年）（全球定位系统、激光雷达、摄像头）。Shenoy等（2019年）提出了一种用于自主系统室内定位的基于人工神经网络的位置估计单元（ANN‐LEU（基于人工神经网络的位置估计单元）），以估计物体在视距（LOS）和非视距（NLOS）条件下的二维（2‐D）位置。当环境存在重复性图案或在农村或森林环境中数据缺乏时，横向定位无法正常工作。

为解决这些局限，需要研究一种结合全局与局部定位的更完整方案。大多数局部定位方法是利用嵌入式摄像头提出的，但大多数现有方法在实际部署场景中并不适用。下一节将介绍并详细阐述现有技术。横向定位是一项更通用功能的一部分，该功能使汽车能够自动驾驶。Che等（2019年）最近提出了一项有趣的工作，聚焦于使用改进的粒子群优化进行路径规划。

在此背景下，我们的研究旨在在复杂挑战性环境中，寻找道路标线检测和车道估计的处理时间与效率之间的平衡。我们提出的主要贡献有两个方面：一是模型在复杂挑战性环境中估计道路标线曲率的有效性和精度；二是将给定图像划分为三个区域的过程（一个区域用于直车道，两个区域用于弯道）。该过程有助于模型参数的良好初始化。

在本研究中，我们关注的是使车辆实现精确横向定位的方法。具体而言，我们感兴趣的是道路标线的检测与估计。由于车道检测任务的重要性，多年来研究人员已针对车道检测开展了大量研究。总体而言，基于视觉的车道检测可分为两大类：直线车道和曲线车道。

本文组织如下：在引言介绍本研究的背景之后，第2节重点讨论现有技术。第3节概述了所提出的方法，包括使用嵌入式摄像头图像进行道路标线检测的所有步骤。第4节详细说明了评估和实验结果。最后，第5节给出了结论和未来工作。

2 相关工作

基于视觉的道路车道检测已经进行了大量的研究。在过去十年中，提出了许多用于直道和弯道车道检测的方法。

2.1 直车道

在内存受限的情况下，用于直车道检测与估计的最有效技术是霍夫变换（HT）（Hassanein等人，2015年；Lopez‐Krahe和Pousset 1988； Mukhopadhyay和Chaudhuri2015年）。该技术已成为人工视觉领域中的标准工具。此步骤通常在通过投影模型获取的原始图像上执行，或在应用逆透视变换后进行（Wu和Chen 2016年）。HT算法的性能在很大程度上取决于数据量。

在Kultanen等人（1990年）和Xu等人（1990年）的研究中，作者提出了一种特殊的霍夫变换，即随机霍夫变换（RHT）。霍夫变换与随机霍夫变换的区别在于，标准霍夫变换将每个单独的像素映射到累加空间，而随机霍夫变换处理的是成对像素，从而管理一个子集。作为一种另一种扩展，概率霍夫变换（PHT）（Guo等人，2008年）以较低的计算成本解决了相同的问题。在Liu等人（2012年）的研究中，提出了渐进概率霍夫变换（PPHT），旨在最小化参与投票的点的比例，同时保持假阴性和假阳性率接近标准霍夫变换的结果。关于二值图像的一些进一步研究，如广义霍夫变换或广义模糊霍夫变换等，可参见Antolovic（2008年）、Chiu等人（2012年）、Izadinia等人（2009年）以及Thomas（1992年）。

在大多数方法中，霍夫变换（HT）已与其他方法结合使用，例如线分类。Cela等人（2013年）提出了一种基于无监督自适应分类器的道路车道检测算法。该算法通过三个步骤来获取车道。第一步，利用输入图像中的亮度信息判断环境条件，并突出彩色车道。第二步应用无监督分类器和霍夫变换（HT），以识别道路的左右边界线。随后应用卡尔曼滤波器来估计车辆位置并进行车道跟踪。Liu等人（2018年）结合了逆透视映射（IPM）和K均值聚类来确定正确的车道，并使用霍夫变换（HT）检测图像中的直线。

Parajuli等人（2013年）提出了一种在阴影和低光照条件下进行车道检测的方法。第一步是利用局部梯度描述符识别相邻左右车道上的点。然后，通过一个简单的线性预测模型，在每个水平条带上检测车道标线点。

其他方法基于颜色特征和霍夫变换以提高效率。在Bottazzi等人（2014年）的研究中，作者提出了一种基于HSV（色调、明度、饱和度）直方图的车道标线检测新方法。使用先前的三角模型确定动态感兴趣区域（ROI）。第一步是计算整幅图像的直方图。通过确定两幅连续图像之间的差异来发现光照变化。从感兴趣区域中分割出车道标记。然后，采用一种跟踪方法（Bouguet 2001）来验证和检测车道。在Li等人的研究（2018年）中，作者提出了一种基于多种特征提取连接的新方法。其主要目标是利用HSV色彩空间提取道路的白色特征。然后，在预处理步骤中加入初步的边缘特征检测。在检测步骤中，同时应用霍夫和坎尼算子。最后，应用卡尔曼滤波器完成线条跟踪。

当施加实时约束时，Lin等人（2010年）提出了一种基于扩展边缘连接算法的新方法。首先初始化一个感兴趣区域，然后使用索贝尔算子找到属于边缘的像素。提出了一种方向性边缘间隙闭合算法，以生成更完整的边缘连接，这些边缘可能属于车道。下一步是检测车道标记的颜色。然后使用霍夫变换对直线模型进行拟合。

2.2 弯曲车道

在弯道车道检测方面，其他研究采用了更复杂的模型，如B样条、抛物线和双曲线（Jung和Kelber 2005； Khalifa等，2010年；Timar和Alagoz2010年）。贝塞尔曲线（Cimurs等，2017年）和B样条（Li等，2017b）被认为是用于弯曲线检测的相关方法，并已被配置以克服曲线插值的缺点（Dagnino等，2015年），这些缺点主要有两点：（1）曲线由多项式定义，而通常参数化表示更具优势；（2）计算成本高，因为多项式阶数随控制点数量成比例增加。

对于采用B样条方法的相同模型，Faizal和Mansor（2009）以及Wang等人（1999）提出了基于B‐蛇技术的算法。该算法能够恢复多种车道，尤其是弯道。B‐蛇是B样条的一种实现，因此可以通过一组控制点形成任意形状。该系统旨在检测道路标线的两侧，通过检测车道内的中心线，然后估计其他平行线来实现。B‐蛇的初始位置由CHEVP算法（坎尼/霍夫消失点估计）确定。接着，为了确定B‐蛇模型的控制点，必须进行最小化步骤。该方法的主要缺点是无法应用于实时场景，而Aly（2008）提出了一种鲁棒且实时的算法用于在城市街道中检测车道。通过逆透视映射生成道路图像的俯视图模型，以减少透视效应。该算法基于使用高斯核进行滤波。类似的思想在Guo等人（2015）中得到了进一步发展，其中提出了一种改进的 RANSAC算法来估计车道模型参数。

对于车道检测，与其使用手工特征提取方法，Lee等人（2019）提出了一种基于改进的卷积神经网络的方法，该方法利用环视图像实现地面车辆的自动驾驶，并在多种不利条件下对高曲率车道进行了评估。实验表明，由于该方法的计算时间较长，车辆速度被限制在7 kph以内才能获得车道线道路检测结果。作者降低了图像采集的帧率以及方向盘控制指令的频率。在Wang等人（2008）的研究中，作者使用双曲线模型进行标线检测。该模型引入了一个非线性项，以处理道路直线和弯曲路段之间的过渡段。模型参数通过消失点进行估计，该消失点对应于双曲线的渐近线。在Chen和Wang（2006）以及Wang和An（2010）的研究中，作者提出了一种基于线性‐双曲线混合模型的算法。其基本思想是将道路标线划分为两个部分：摄像头附近的近处区域和远处区域。这两个区域的曲线检测均基于线性‐双曲线模型。对于近处区域，由于假设车道为直线，因此采用霍夫变换方法；而对于远处区域，则使用双曲模型来处理线条弯曲的情况。该模型需要估计的最重要参数是曲率程度，如下方双曲模型的方程所示：

$$
(1)\quad y = \frac{a}{x - h} + b(x - h) + v
$$

在（2）中，x、y是道路标线点的像素坐标，a是双曲线的曲率参数，b是直线车道标线的斜率，而（h, v）是消失点的坐标向量。Tan等人（2014年）提出了一种方法，该方法采用双曲线模型，并通过引入“河流流法”（Lim等人 2012）进行改进，以在复杂条件下检测弯曲车道，包括虚线标线和车辆遮挡。为了确定曲率系数，Tan等人（2015年）提出了一种名为“改进的河流流法”的新方法，用于搜索远场中对应于车道标线的特征点。

在Jang等人（2014年）中，提出了另一种基于几何模型的方法。该方法的基本思想是应用两个主要步骤：第一步涉及道路特征的提取，第二步依赖于几何模型进行车道检测。通过应用投票系统来检测候选线，并提取最符合车道的一条。在Chen和He（2012）中，作者提出了一种使用最大似然原理检测急弯车道的方法。

第三类方法基于用于车道提取的学习技术。例如，在Fan等人（2013年）中，作者提出了一种基于改进的提升算法的车道检测算法，该算法使用分类函数来判断每个点是否为车道线的边缘点。Kim等人（2017年）使用一种基于极限学习机（ELM）的卷积神经网络（CNN）新学习算法进行图像增强和车道检测。在Kim和Lee（2014年）中，作者使用卷积神经网络去除图像中的噪声，然后使用RANSAC算法拟合车道。Kim和Park（2017a）提出了一种顺序端到端迁移学习方法——两次迁移学习，用于估计左右车道，无需任何后处理。Li等人（2017a）提出了一种基于深度学习的检测模型。设计了一种基于循环神经网络（RNN）和卷积神经网络的多任务网络结构，用于检测车道边界，包括无标记区域，且无需任何显式先验知识或二次建模。

根据上述文献综述，我们可以得出结论：大多数现有的直线和弯道车道检测方法仅在高质量图像上表现良好。此外，急转弯车道的检测仍然是一个具有挑战性的问题。使用双曲表示的参数模型在车道检测质量和参数估计方面效率最高。在本研究中，我们聚焦于这些模型，以提出一种新颖的弯道车道特征化与估计方法。

下一节将详细介绍所提出的方法。

3 提出的方法

我们在此详细说明用于弯曲车道估计的所提出方法。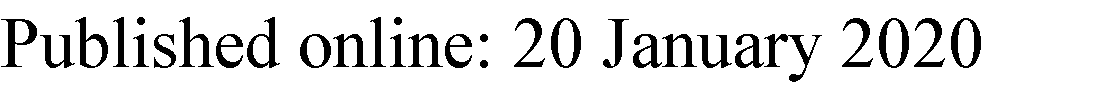示意图0

输入图像经过一个预处理步骤，以执行轮廓提取，如Fakhfakh等人（2018）所述。然后，目标是通过将提取的车道拟合到所采用的解析模型来表征它们。具体而言，假设弯曲线在局部遵循式（1）中的双曲模型。因此，图像被分解为N个水平区域，如图2所示，每个区域关联一条不同的双曲线。区域数量（N）通过经验选择。每幅图像从地平线到图像底部被划分为三个（3）不同区域（近、中、远区域），并对每个区域应用该模型以估计曲率参数。这样做的动机在于，根据透视几何，曲率在图像中并非恒定。一个贝叶斯模型被提出用于估计N条双曲线的超参数，从而在整个图像上准确表征弯曲车道。实际上，由于贝叶斯模型具有灵活性和高度自动化的特点，它们在信号与图像文献中正被越来越多地使用（Andrieu 1998；Roumeliotis和Bekey 2000；Shiffrin等人 2008）。在此背景下，通常采用 MCMC采样来进行推断（Cowles和Carlin 1996； Merali和Barfoot 2013）。

3.1 采用的模型

根据我们上述的现有技术，我们注意到Lim等人（2012）以及Tan等人（2014、2015）提出的基于双曲线道路模型的方法相比其他方法（抛物线模型、B‐蛇模型、几何模型等）具有更高的道路建模精度。该模型能够在复杂环境条件下满足自动驾驶车辆用户的需求。采用这一解析模型，对弯曲车道的表征可简化为估计公式（1）中涉及的超参数。

在本文中，我们将曲线车道的表征重新表述为一个反问题。具体而言，考虑了一个去噪问题，其中式 (1)中双曲线车道模型的坐标y被假设为第二个坐标x的观测值。考虑到图像的水平分解为N个区域，并对属于车道的每个像素，采用以下观测模型

$$
(2)\quad y=\left[\sum_{i=0}^{N-1}\left(\frac{a_i}{x-h_i}+b_i(x-h_i)+v_i\right)1_{[c_i,c_{i+1}]}(x)\right]+n
$$

其中n是一个假设为高斯的噪声项，$1_{[c_i,c_{i+1}]}$是指示函数，在区间$[c_i,c_{i+1}]$上等于1，否则为0。

为了便于表示，我们采用以下符号表示：
- $\mathbf{a}={a_0,…,a_{N-1}}$ 是分组参数$a_i$的向量；
- $\mathbf{b}={b_0,…,b_{N-1}}$ 是分组参数$b_i$的向量；
- $\mathbf{h}={h_0,…,h_{N-1}}$ 是分组参数$h_i$的向量；
- $\mathbf{v}={v_0,…,v_{N-1}}$ 是分组参数$v_i$的向量；
- $\mathbf{c}={c_0,…,c_N}$ 是分组参数$c_i$的向量。

因此，该方法的目标是基于观测到的坐标向量$\mathbf{y}={y_1,…,y_L}$和$\mathbf{x}={x_1,…,x_L}$来估计超参数向量$\mathbf{a},\mathbf{b},\mathbf{h}$和$\mathbf{v}$，其中$L$是用于表征车道的像素数量。

3.2 分层贝叶斯模型

我们提出使用贝叶斯模型来估计超参数向量$\boldsymbol{\theta}={\mathbf{a},\mathbf{b},\mathbf{h},\mathbf{v},\sigma}$。为此，假设超参数向量$\mathbf{a}$、$\mathbf{b}$、$\mathbf{h}$和$\mathbf{v}$分别是随机变量A、B、C、H和V的实现。接下来，我们将详细介绍所采用的似然和先验模型。

3.2.1 似然

基于所采用的观测模型，其中假设扰动n为具有方差$\sigma^2_n$的高斯分布，似然可以表示为

$$
(3)\quad f(\mathbf{y}|\mathbf{a},\mathbf{b},\mathbf{h},\mathbf{v},\sigma,\mathbf{c}) \propto \prod_{l=1}^{L} \exp\left[-\frac{1}{2\sigma_n^2}\left|y_l-\sum_{i=0}^{N-1}\left(\frac{a_i}{x_l-h_i}+b_i(x_l-h_i)+v_i\right)1_{[c_i,c_{i+1}]}(x_l)\right|^2\right]
$$

3.2.2 超参数先验

假设$N$条双曲线之间的独立性，我们为每条$a_i$关联一个逆伽玛（IG）先验：

$$
(4)\quad f(a_i|\alpha_a,\beta_a)=IG(a_i|\alpha_a,\beta_a) \propto (a_i)^{-1-\alpha_a}\exp\left(-\frac{\beta_a}{a_i}\right)
$$

考虑到N条双曲线，联合先验可写为

$$
(5)\quad f(\mathbf{a}|\alpha_a,\beta_a) \propto \prod_{i=0}^{N-1} f(a_i|\alpha_a,\beta_a)
$$

形状和尺度参数（$\alpha_a$和$\beta_a$）可以手动设置，也可以通过在其上添加超先验进行估计。值得注意的是，逆伽玛先验是建模实正变量的常见选择。

由于$\mathbf{b}$、$\mathbf{h}$和$\mathbf{v}$均为实正数，因此采用了与$\mathbf{a}$相同的方法来定义所需的先验：

$$
f(\mathbf{b}|\alpha_b,\beta_b)= \prod_{i=0}^{N-1} IG(b_i|\alpha_b,\beta_b),\quad f(\mathbf{h}|\alpha_h,\beta_h)= \prod_{i=0}^{N-1} IG(h_i|\alpha_h,\beta_h),\quad f(\mathbf{v}|\alpha_v,\beta_v)= \prod_{i=0}^{N-1} IG(v_i|\alpha_v,\beta_v)
$$

关于超参数$\mathbf{c}$，对每个$c_i$采用区间$[0, M]$上的均匀分布，其中$M= \max{x_1,…, x_L}$：

$$
(6)\quad f(\mathbf{c})= \prod_{i=0}^{N} f(c_i)= \prod_{i=0}^{N} U 0,M
$$

为简化起见，假设噪声方差$\sigma^2_n$固定为一个较小的值，以模拟较低的扰动水平。然而，该超参数也可以通过设定合适的先验（例如Jeffrey先验）来估计，并将其纳入分层模型中。

3.3 贝叶斯推理

贝叶斯推理在此用于推导估计量$\hat{\mathbf{a}}$、$\hat{\mathbf{b}}$、$\hat{\mathbf{h}}$和$\hat{\mathbf{v}}$。

3.3.1 提出的吉布斯采样器

采用最大后验（MAP）方法，需要将上一节中详细描述的似然和先验结合起来，以推导出后验分布并计算目标估计量。记$\boldsymbol{\theta}={\mathbf{a},\mathbf{b},\mathbf{h},\mathbf{v},\mathbf{c}}$为目标参数向量，$\boldsymbol{\phi}={\alpha_a, \beta_a, \alpha_b, \beta_b, \alpha_h, \beta_h, \alpha_v, \beta_v}$为联合后验分布，其表达式为

$$
(7)\quad f(\boldsymbol{\theta}|\mathbf{x},\mathbf{y},\boldsymbol{\phi}) \propto f(\mathbf{y}|\mathbf{a},\mathbf{b},\mathbf{h},\mathbf{v},\sigma,\mathbf{c})f(\mathbf{a}|\alpha_a, \beta_a)f(\mathbf{b}|\alpha_b, \beta_b)f(\mathbf{h}|\alpha_h, \beta_h)f(\mathbf{v}|\alpha_v, \beta_v)f(\mathbf{c})
$$

此处的目标是基于公式(7)中的联合后验分布来估计参数和超参数向量$\boldsymbol{\theta}$和$\boldsymbol{\phi}$。然而，显然该后验分布难以处理，因此推导出$\boldsymbol{\theta}$和$\boldsymbol{\phi}$的解析估计量是一项复杂的任务。为此，我们采用一种MCMC采样方案，具体来说是使用吉布斯采样器，从条件分布$f(\mathbf{a}|\mathbf{x},\mathbf{y},\boldsymbol{\theta}),f(\mathbf{b}|\mathbf{x},\mathbf{y},\boldsymbol{\theta})$，$f(\mathbf{h}|\mathbf{x},\mathbf{y},\boldsymbol{\theta})$以及$f(\mathbf{v}|\mathbf{x},\mathbf{y},\boldsymbol{\theta})$进行数值采样。

其原理是通过对其他变量积分，推导出每个未知参数（在$\boldsymbol{\theta}$和$\boldsymbol{\phi}$中）的条件分布。然后利用这些条件分布通过解析计算或借助数值模拟技术来获得估计量。如前所述，此处我们采用基于MCMC采样方案的数值采样方法。所提出的吉布斯采样器总结于算法1中。

算法 1：提出的混合吉布斯采样器。

用某些$a^0$, $b^0$, $h^0$, $v^0$, $c^0$初始化。

当未收敛时执行
采样$\mathbf{a}^{(r)} \sim f(\mathbf{a}|\mathbf{x},\mathbf{y},\boldsymbol{\theta})$
采样$\mathbf{b}^{(r)} \sim f(\mathbf{b}|\mathbf{x},\mathbf{y},\boldsymbol{\theta})$
采样$\mathbf{h}^{(r)} \sim f(\mathbf{h}|\mathbf{x},\mathbf{y},\boldsymbol{\theta})$
采样$\mathbf{v}^{(r)} \sim f(\mathbf{v}|\mathbf{x},\mathbf{y},\boldsymbol{\theta})$
采样$\mathbf{c}^{(r)} \sim f(\mathbf{c}|\mathbf{x},\mathbf{y})$
end

预热期至关重要，以确保吉布斯采样能够达到收敛。随后利用采样链 $[(\mathbf{a}^{(r)}) {1\le r \le R}, (\mathbf{b}^{(r)}) {1\le r \le R}, (\mathbf{h}^{(r)}) {1\le r \le R}, (\mathbf{v}^{(r)}) {1\le r \le R}, (\mathbf{c}^{(r)})_{1\le r \le R}]$ 和通过例如最小均方误差（MMSE）估计量来推导估计量。对应于预热期的样本将被丢弃。

下文提供了不同的条件分布。

3.3.2 条件分布

为了推导与模型各个参数相关的条件分布，需要对(7)中的联合后验分布关于所有其他参数进行积分。关于超参数$a_i$，基于(7)的计算得到如下形式

$$
(8)\quad f(a_i|\mathbf{a} {-i},\mathbf{b},\mathbf{h},\mathbf{v},\mathbf{c},\mathbf{x},\mathbf{y}) \propto \prod {l=1}^{L} \exp\left[-\frac{1}{2\sigma_n^2}\left|y_l-\sum_{i=0}^{N-1}\left(\frac{a_i}{x_l-h_i}+b_i(x_l-h_i)+v_i\right)1_{[c_i,c_{i+1}]}(x_l)\right|^2\right] \times (a_i)^{-1-\alpha_a} \exp\left(-\frac{\beta_a}{a_i}\right)
$$

通过分析该条件分布的表达式，发现无法将其与标准分布（高斯、伽马、贝塔等）相匹配。由于即使所得到的分布属于指数族，也无法进行直接采样，因此采用Metropolis‐Hastings (MH) 算法对该后验分布进行采样。

由于所用先验的相似性，通过对(7)分别关于$b_i$、$h_i$、$v_i$和$c_i$积分，可得到$f(b_i|\cdot)$、$f(h_i|\cdot)$、$f(v_i|\cdot)$和$f(c_i|\cdot)$的相同类型的条件分布。实际上，这些分布形式相似是预期的，其指数结构部分由采用的高斯似然所决定。为了简洁起见，此处不详细列出这些条件分布的完整表达式。针对这些条件分布的采样通过MH步骤实现。

4 实验结果

在本节中，所提出的方法通过合成数据和真实数据对弯道车道特征进行验证，以评估其性能。

4.1 模拟数据

在第一次实验中，所提出的算法在合成数据上进行了测试，以验证其有效性。每幅图像被划分为三个区域（N= 3），其中每个区域估计一条双曲线（第一个区域除外，该区域估计一条直线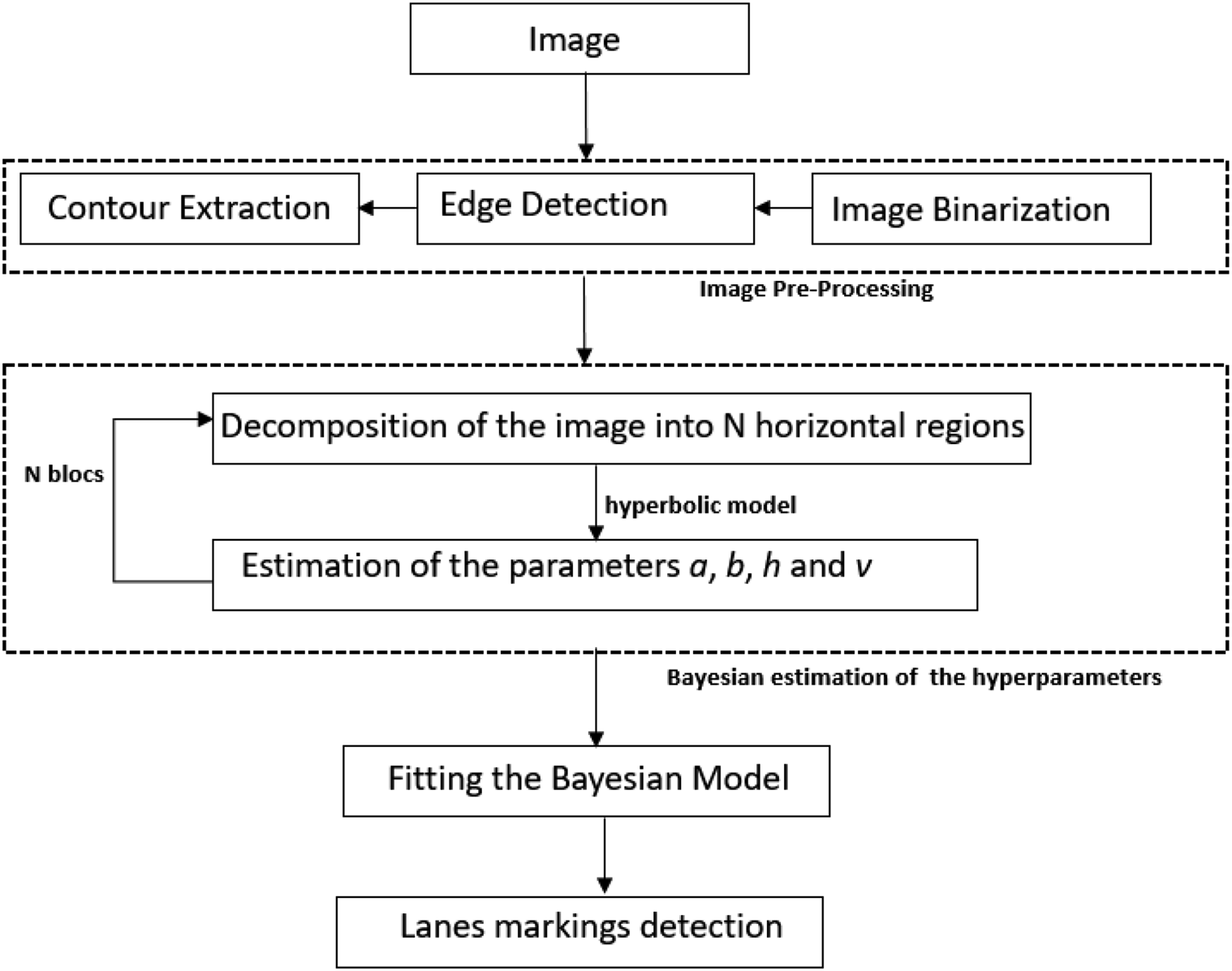）。示意图1

基于可获得实际道路标线的真实值，仿真按照公式 (2)中的观测模型进行。为了验证算法收敛后模型的精度（处理时间和各超参数的估计值），有必要测试方差的不同取值$\sigma^2_n$。

为此，我们选择测试三个不同的方差值$\sigma^2_n = 30$、$\sigma^2_n = 15$和$\sigma^2_n = 5$。这使我们能够测量数据的高斯扰动对算法性能的影响，并在不同程度的实验条件下进行验证。每条双曲线的参数随后通过所提出的混合吉布斯采样器进行估计。共需要30,000次迭代以获得目标估计量，其中前15,000次迭代作为预热期以达到收敛。

收敛后，表1、2和3报告了所有参数的估计值，并将其与真实值进行比较。同时提供了每个参数估计的误差率。每张表格均包含各区域的理论值和估计值，以便对比所得结果。所考虑的真实值（来自图3的图像）对应的超参数向量为

$$
\boldsymbol{\theta}={\mathbf{a}=[200,1500,7500],\mathbf{b}=[0.3, 0.5,0.7],\mathbf{h}=[430,400,390],\mathbf{v}=[680,680,680]}
$$

我们发现，在算法收敛后，每次降低方差值$\sigma^2_n$，平均误差和最小误差也随之减小。如表格所示，不同误差值在$\sigma^2_n = 30$时的平均误差约为3.64%，最小误差为2.31%，而在$\sigma^2_n = 5$时分别降至1.43%和0.87%以下。报告的数值明确表明了所提出方法在精确估计相关参数，从而准确地刻画不同的双曲线。

道路车道估计中最具有挑战性的情况是靠近地平线处的急弯。双曲模型的所有参数都相当重要，但参数’a’仍然是最值得关注的，需要仔细且精确地估计。随着接近地平线，参数’a’的变化应当非常敏感：对参数’a’的错误估计可能导致曲率的严重错误估计。

多次运行Gibbs采样算法后，差异结果展示了对估计参数的评估。向量（theta）的超参数实际值大约在97%的置信区间内。所获得的不同值非常可靠，并且接近真实值的初始结果。通常，在远距离区域估计车道标线的曲率参数尤其困难，特别是在强曲率情况下。如表1、2和3所示，我们发现参数“a”的置信度非常令人鼓舞，其误差率在1%到3%范围内，针对不同的$\sigma^2_n$，这表明了我们的估计量具有较高的准确性。对于其他参数“b”、“h”和“v”，同样表现出良好性能，它们非常接近理论值，误差率低于3%。

表1 双曲线参数 $\sigma^2_n= 30$ ：估计值和参考值
参数	真实值	估计值	错误率（%）
a1	200	186	1.14
b1	0.3	0.15	2.07
h1	430	412	0.38
v1	680	523	1.41
a2	1500	1452	2.42
b2	0.5	0.36	2.25
h2	400	398	0.67
v2	680	651	0.58
a3	7500	7364	3.48
b3	0.7	0.37	5.11
h3	390	348	0.91
v3	680	646	0.92

平均误差为3.64%，最小误差为2.31%

表2 双曲线参数用于 $\sigma^2_n = 15$ ：估计值和参考值
参数	真实值	估计值	错误率（%）
a1	200	173	0.39
b1	0.3	0.19	1.05
h1	430	424	0.11
v1	680	551	1.01
a2	1500	1447	1.67
b2	0.5	0.39	1.35
h2	400	302	1.21
v2	680	664	0.10
a3	7500	7474	2.42
b3	0.7	0.52	3.08
h3	390	373	2.98
v3	680	662	0.31

平均误差为2.67%，最小误差为1.06%
| 表3 双曲线参数用于 $\sigma^2_n= 5$ ：估计值和参考值 | | | |
| :— | :— | :— | :— |
| 参数 | 真实值 | 估计值 | 错误率（%） |
| a1 | 200 | 189 | 0.11 |
| b1 | 0.3 | 0.24 | 0.66 |
| h1 | 430 | 426 | 0.09 |
| v1 | 680 | 573 | 0.08 |
| a2 | 1500 | 1488 | 0.83 |
| b2 | 0.5 | 0.38 | 1.07 |
| h2 | 400 | 376 | 0.65 |
| v2 | 680 | 602 | 1.17 |
| a3 | 7500 | 7489 | 1.14 |
| b3 | 0.7 | 0.63 | 0.89 |
| h3 | 390 | 313 | 1.31 |
| v3 | 680 | 592 | 0.40 |

平均误差为1.43%，最小误差为0.87%

4.2 真实数据

本文所述的车道标线检测算法已在Intel i7，2.40 GHz CPU上实现。该算法在具有可用真实值的 ROMA数据集上进行了评估（Veit等，2008年）。该数据库包含在各种不同条件下采集的异构真实道路图像（全阴影或部分阴影、不同的光照条件等）。参数 N，即从地平线到图像底部的水平区域数量，根据经验设置为3。在底部区域，线条通常为直线，而从第二区域到顶部区域曲率逐渐增加。实际上，N= 3的选择依据是图像顶部与底部之间曲率水平的渐变特性。

除了ROMA数据集具有挑战性的实际图像外，道路标线对应的真实值的可获得性为我们提供了评估车道检测和曲率估计的最佳机会。车道检测部分已在先前的研究中进行了深入评估，并使用了与该实验相同的数据库（Fakhfakh et al. 2018年）。

对于不同场景和实验条件，图4展示了我们的方法在不同实验条件下的车道特征化性能，例如高光照、阴影、急弯等情况。图4中的红线表示我们的算法对车道和曲率估计的输出结果，与真实的道路标线重叠。

示意图2

我们方法的创新性和新颖性在于能够自动估计道路上每个区域双曲模型的所有参数，而不同于现有技术中的其他工作通常通过划分为两部分来估计曲率程度。本图中报告的结果清楚地展示了所提出方法在自动估计每个区域的不同双曲模型参数方面的创新性和良好性能，从而准确地表征车道。值得注意的是，这些结果是使用与模拟数据相同的迭代次数和预热期获得的，在所使用的架构上对应的计算时间为10秒。

为了定量评估我们的方法的性能，计算了真正率（TPR）和假正率（FPR）以便与其他最先进的方法进行比较，特别是Guo等人（2015）和Tan等人（2015）的工作（详见第2节）。报告的数值清楚地表明，所提出的方法在定量方面优于其他方法。如表4所示，TPR指标明显优于其他对比方法，且FPR更低。由于摄像头的透视几何模型，通过提高图像分辨率或在不同的图像空间表示中应用该方法（例如俯视图模型），可以进一步精确改进最远区域的曲率估计。

表4 所提方法与Guo等人（2015 年）以及Tan等人（2015年）的研究中的真正率和假正率值
帧	郭等人提出的方法（2015年）		Tan等人提出的方法（2015年）		我们的方法
	TPR（%）	FPR（%）	TPR（%）	FPR（%）	TPR（%）	FPR（%）
1	85.68	11.36	87.29	10.12	93.24	7.39
2	93.91	4.02	94.41	3.88	95.20	4.52
3	87.08	14.21	86.73	14.51	89.07	12.46
4	83.18	29.98	85.04	21.03	88.67	15.37
5	94.64	7.59	93.62	7.79	93.39	5.64
6	89.54	10.74	90.33	9.34	91.45	7.89
平均值	89.01	12.98	89.57	11.11	91.83	8.87