整数倍内插

最新推荐文章于 2024-05-28 21:28:00 发布

原创

最新推荐文章于 2024-05-28 21:28:00 发布 · 2.7k 阅读

26 ·

CC 4.0 BY-SA版权

该博客通过Matlab代码展示了整数倍内插（零值内插）结合低通滤波在信号处理中的应用。以一个100Hz正弦波为例，初始采样频率为400Hz，进行8倍内插后，再通过低通滤波器处理，揭示了内插和滤波如何改变信号的时域波形和频谱特性，有助于理解信号重构和采样率转换的过程。

整数倍内插是先在已知抽样序列的相邻点之间等间隔地插入（I-1）零值点然后进行低通滤波，即可求得I倍内插的结果。整数倍零值内插当然不能简单的等同于提高了数据采样频率，但经过零值内插的数字信号，其频谱一定是增加了I倍。

假设模拟信号在0~1KHz的频段内有信号，利用2KHz的频率进行A/D采样，则采样后的信号没有频谱混叠，频谱周期为2KHz，信号频谱如下图（a）所示。根据零值内插规则，对采样数据进行2倍零值内插后，其信号频谱如下图（b）所示。
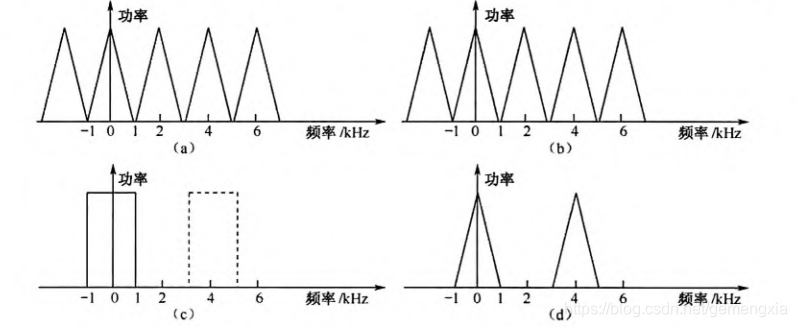
在这里插入图片描述
需要注意：插值前的信号采样率为2KHz，频谱周期为2KHz，零值内插后信号速率为4KHz，频谱周期为4KHz。如果在零值内插后增加一级低通滤波器，其截止频率为1KHz，则滤波后的频谱周期依然为4KHz，只是滤掉了频率在1~3KHz之间频谱成分，则滤波后的信号频谱变成了图中（d）所示。也就是说，经过零值内插、低通滤波处理后，即可得到正确的经高速采样后的数字信号。

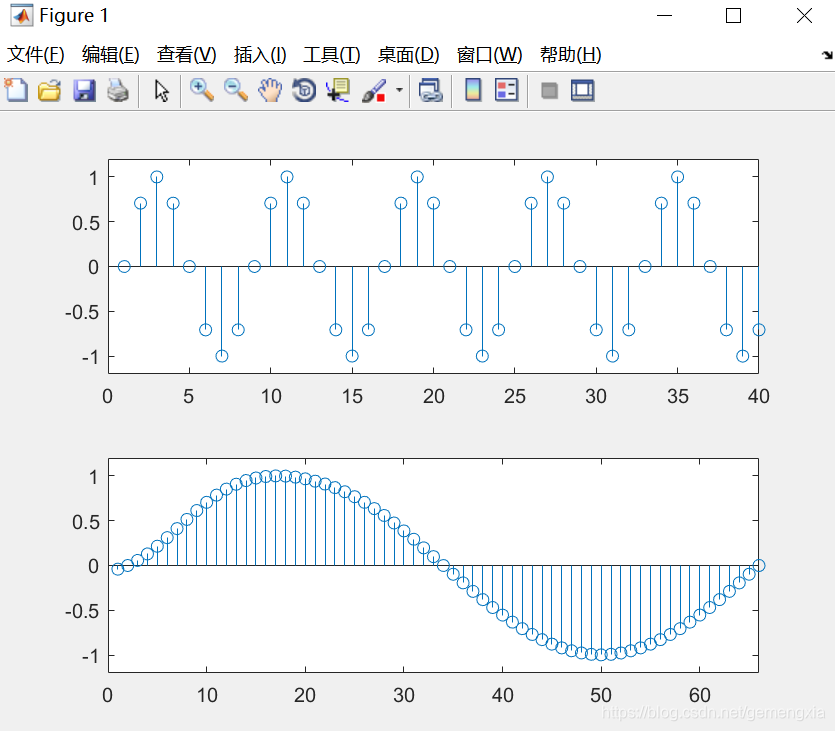
8倍内插前后仿真时域波形
在这里插入图片描述
源码：

%E6_2_InterSpec.m文件源代码
%用Matlab仿真整数倍内插过程的信号变换关系。假设原始信号为频率为100Hz的正弦波，初始采样频率为400Hz。仿真对信号进行4倍内插后的信号波形
%图。比较内插前后信号的时域波形变化。

%定义参数
f=100;       %信号频率为100Hz
Fs=800;      %采样频率为400Hz
I=8;         %内插倍数

%产生信号
t=0:1/Fs:0.5;
c=2*pi*f*t;
si=sin(c);%产生正弦波

%进行4倍零值内插处理
Isi=zeros(1,length(si)*I);
Isi(1:I:length(Isi))=si;

%经低通滤波器处理
b=<