学习摘自数字芯片实验室
1、 如下图所示的一个LFSR结构,初值如图所示,在4个时钟周期之后,寄存器中的值从左到右的16进制表示为?
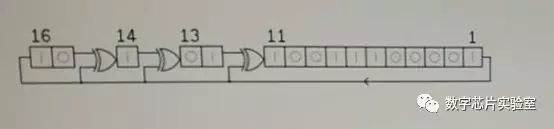
变化前:X[16]、X[15]、X[14] 、X[13] 、X[12]、X[11] 、X[10]、X[9] 、X[8]、X[7]、X[6]、X[5]、X[4]、X[3]、X[2]、X[1]
变化后:X[1] 、X[16]、X[15]^ X[1]、X[14] ^ X[1]、X[13]、X[12] ^ X[1]、X[11]、X[10]、X[9]、X[8]、X[7]、X[6]、X[5]、X[4]、X[3]、X[2]
初值:10_1_01_10011100001
根据上述关系,进行4个周期的转换,然后用16进制表示
2、下图中的一个三级反相器链,第一级反相器的输入电容Ci = 4fF,最后一级反相器的负载电容CL = 32fF,为使整个反相器链的延迟最小,如果第一级反相器的大小为1,第二级反相器的大小应为?第三级反相器的大小应为?
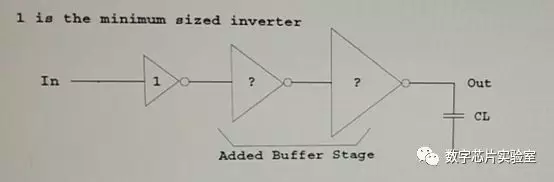
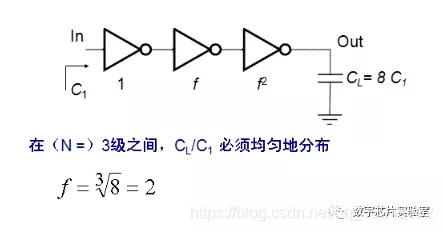
f = 2, 所以第二级反相器的大小应为2,第三级反相器的大小应为4
3、下图的电路中,flip-flop2的setup time margin = ? ns、
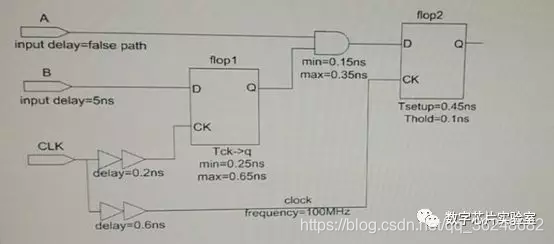
Tmargin = 10ns + 0.6ns -0.2 ns– 0.65 ns –0.35 ns – 0.45 ns = 8.95ns
建立时间余量,100M即10ns
4、下图中的电路,器件延迟如图中标注,将框内的电路作为一个寄存器,其有效setup time = ? ns,hold time = ? ns
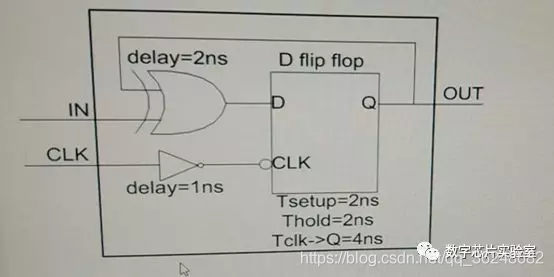
有效setup time分析:
对于D触发器而言,Tsetup = 2ns,也就是说数据信号需要提前时钟信号2ns到达触发器D端。
- 1
考虑时钟路径延迟,Tsetup_valid = Tsetup - 1ns = 1ns ;
在考虑数路径延迟:Tsetup_valid = Tsetup - 1ns +2ns = 3ns ;
有效hold time分析:
对于D触发器而言,Thold = 2ns,也就是说数据信号需要在时钟信号到达后保持2ns
- 1
考虑时钟路径延迟,Thold_valid = Thold + 1ns = 3ns ;
在考虑数路径延迟:Thold_valid = Thold + 1ns -2ns = 1ns ;
前几天参加乐鑫的笔试,遇到一道题目,很有价值,分享给大家。
题目要求:将一个串行执行的C语言算法转化为单拍完成的并行可综合verilog。
C语言源码如下:
unsignedcharcal_table_high_first(unsignedcharvalue)
{
unsigned char i ;
unsigned char checksum = value ;
for (i=8;i>0;--i)
{
if (check_sum& 0x80)
{
check_sum = (check_sum<<1) ^ 0x31;
}
else
{
check_sum = (check_sum << 1);
}
}
return check_sum;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
算法C语言实现:
#include<stdio.h>
int main(){
unsignedchar cal_table_high_first(unsignedcharvalue);
unsignedchar data;
for (unsignedchar i = 0; i < 16;++i)
{
data= cal_table_high_first(i);
printf("value =0x%0x:check_sum=0x%0x \n", i, data);
}
getchar();
}
unsignedchar cal_table_high_first(unsignedcharvalue)
{
unsignedchar i;
unsigned char check_sum = value;
for (i = 8; i > 0;–i)
{
if (check_sum &0x80)
{
check_sum= (check_sum << 1) ^ 0x31;
}
else
{
check_sum= (check_sum << 1);
}
}
return check_sum;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
输出结果:
value =0x0:check_sum=0x0
value =0x1:check_sum=0x31
value =0x2:check_sum=0x62
value =0x3:check_sum=0x53
value =0x4:check_sum=0xc4
value =0x5:check_sum=0xf5
value =0x6:check_sum=0xa6
value =0x7:check_sum=0x97
value =0x8:check_sum=0xb9
value =0x9:check_sum=0x88
value =0xa:check_sum=0xdb
value =0xb:check_sum=0xea
value =0xc:check_sum=0x7d
value =0xd:check_sum=0x4c
value =0xe:check_sum=0x1f
value =0xf:check_sum=0x2e
C语言作为参考模型,用于后续Verilog的功能仿真。
该算法逻辑如下:
输入一个8bit的数,首先判断最高位是否为1,如果为1则左移一位,并且和8‘b00110001异或;如果最高位不为1则左移一位。此过程执行8次。
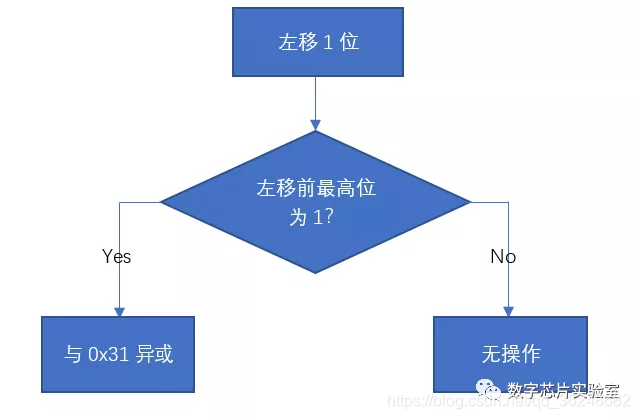
此时我们来看一下异或操作的真值表
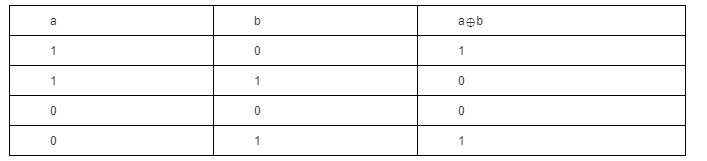
我们可以看出:任何数与0异或都等于它本身,即0^x=x。所以我们可以把算法流程变换为:
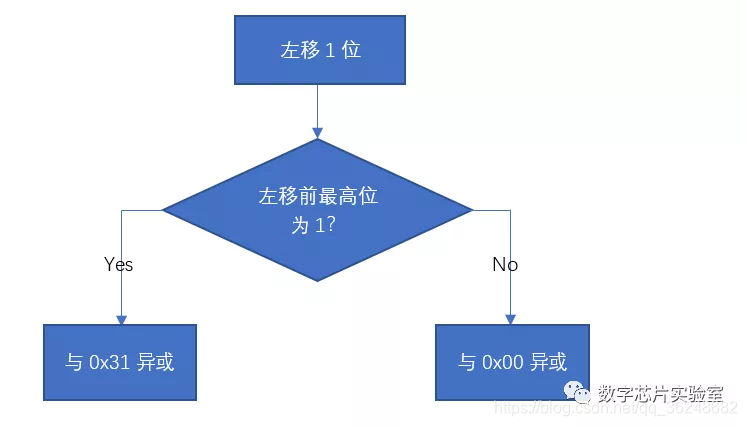
8’h31 = 8’b00110001, 8’h00 = 8’b00000000,设左移前最高位为M,可以将判断左移前最高位是否为1的过程省略,直接与8’b00MM000M异或,此时流程图可以简化为:
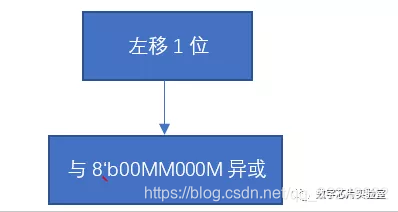
由此,我们可以将循环解开,设输入为一个8bit数C[7:0],下面为解循环过程。
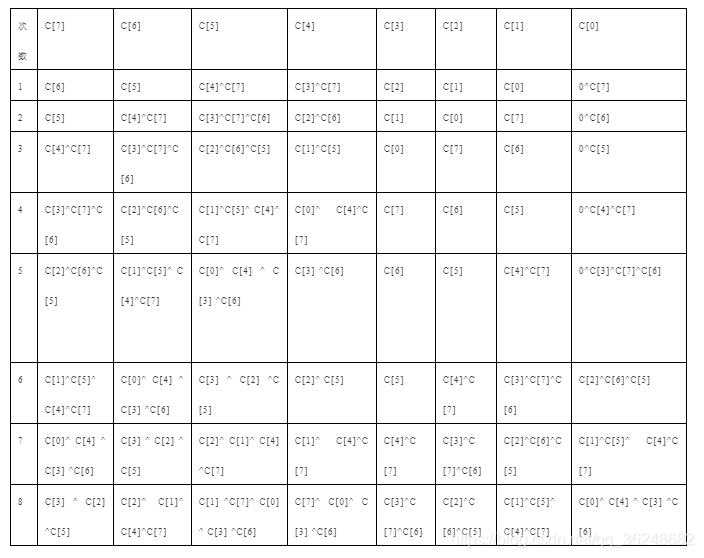
根据上述结果,可以用verilog描述。
module loop1(
input clk,
input rst_n,
input [7:0] check_sum,
output reg [7:0] check_sum_o
);
//reg [7:0] check_sum_o;
always @ (posedge clk or negedge rst_n)
if(!rst_n)
begin
check_sum_o<= 8'h0;
end
else
begin
check_sum_o[7]<= check_sum[3]^check_sum[2]^check_sum[5];
check_sum_o[6]<= check_sum[2]^check_sum[1]^check_sum[4]^check_sum[7];
check_sum_o[5]<= check_sum[1]^check_sum[7]^check_sum[0]^check_sum[3]^check_sum[6];
check_sum_o[4]<= check_sum[7]^check_sum[0]^check_sum[3]^check_sum[6];
check_sum_o[3]<= check_sum[3]^check_sum[7]^check_sum[6];
check_sum_o[2]<= check_sum[2]^check_sum[6]^check_sum[5];
check_sum_o[1]<= check_sum[1]^check_sum[5]^check_sum[4]^check_sum[7];
check_sum_o[0]<= check_sum[0]^check_sum[4]^check_sum[3]^check_sum[6];
end
endmodule
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
testbench:
module loop1_tb;
reg clk;
reg rst_n;
reg [7:0] check_sum;
wire [7:0] check_sum_o;
always #1 clk=~clk;
initial
begin
clk = 0;
rst_n = 0;
#10
rst_n = 1;
for (check_sum=0;check_sum<16;check_sum=check_sum+1)
begin
#2
//check_sum = i;
$display ("check_sum = %h",check_sum_o);
if (check_sum == 15) $stop;
end
//$stop;
end
loop1 loop1_i1(
.clk(clk),
.rst_n(rst_n),
.check_sum(check_sum),
.check_sum_o(check_sum_o)
);
endmodule
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
打印结果为:
check_sum = 00
check_sum = 31
check_sum = 62
check_sum = 53
check_sum = c4
check_sum = f5
check_sum = a6
check_sum = 97
check_sum = b9
check_sum = 88
check_sum = db
check_sum = ea
check_sum = 7d
check_sum = 4c
check_sum = 1f
check_sum = 2e
loop2.v的实现和loop1.v类似,只是代码量更少。
module loop2(
input clk,
input rst_n,
input [7:0] check_sum,
output reg [7:0] check_sum_o
);
integer i;
//reg [7:0] check_sum_o;
reg [7:0] ccc;
always @ (posedge clk or negedge rst_n)
if(!rst_n)
begin
check_sum_o= 8'h0;
end
else
begin
ccc = check_sum;
for(i=0;i<8;i=i+1)
begin
ccc ={ccc[6:0],1'b0}^({8{ccc[7]}} & 8'h31);
end
check_sum_o = ccc;
end
endmodule
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
其实也可以将C语言函数封装成Verilog的function,然后在在单周期内进行赋值。
module loop3(
input clk,
input rst_n,
input [7:0] check_sum,
output reg [7:0] check_sum_o
);
integer i;
function [7:0] cal_table_high_first;
input[7:0] value;
reg[7:0] ccc ;
reg[7:0] flag ;
begin
ccc= value;
for(i=0;i<8;i=i+1)
begin
flag= ccc & 8’h80 ;
if(flag!= 0 ) ccc = (ccc <<1) ^ 8’h31 ;
elseccc = (ccc <<1) ;
end
cal_table_high_first<span class="token operator">=</span> ccc<span class="token punctuation">;</span>
end
endfunction
always @ (posedge clk or negedge rst_n)
if(!rst_n)
begin
check_sum_o= 8’h0;
end
else
begin
check_sum_o<= cal_table_high_first(check_sum) ;
end
endmodule
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
综上,loop1.v和loop2.v的主要贡献是解开了算法实现的if-else判断。至于loop3.v中,将C语言描述的功能封装成fucntion,直接单周期完成赋值的实现方式在逻辑综合后是否增加了if-else判断语句的硬件开销不在本文讨论范围内。
这和设计者施加的时序约束和综合工具算法有关。
</div><div data-report-view="{"mod":"1585297308_001","dest":"https://blog.youkuaiyun.com/qq_36248682/article/details/105289784","extend1":"pc","ab":"new"}"><div></div></div>
<link href="https://csdnimg.cn/release/phoenix/mdeditor/markdown_views-ff98e99283.css" rel="stylesheet">
</div>





















 7712
7712

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








