稀疏矩阵向量乘法的openmp并行优化

稀疏矩阵向量乘法

添加链接描述本人在这篇博客已经介绍过稀疏矩阵向量乘法以及相关的一些存储方式，这里重点开始介绍openmp的并行优化。
下面这个图片就是采用CSR格式读取稀疏矩阵向量乘法的主体架构，全称为Compressed Sparse Row Matrix压缩稀疏矩阵行格式，该格式对矩阵进行行压缩，通过row_ptr,col_ind,values来确定矩阵。对于第i行来说，该行非零元素的列索引存储在col_ind[row_ptr[i]:row_ptr[i + 1]]中，该行非零元素值存储在values[row_ptr[i]:row_ptr[i + 1]]中。可以看出，row_ptr的长度为matrix row + 1，col_ind,val_ind长度为矩阵非零元素个数。CSR格式经常用于读取稀疏矩阵以后计算，运算高效。

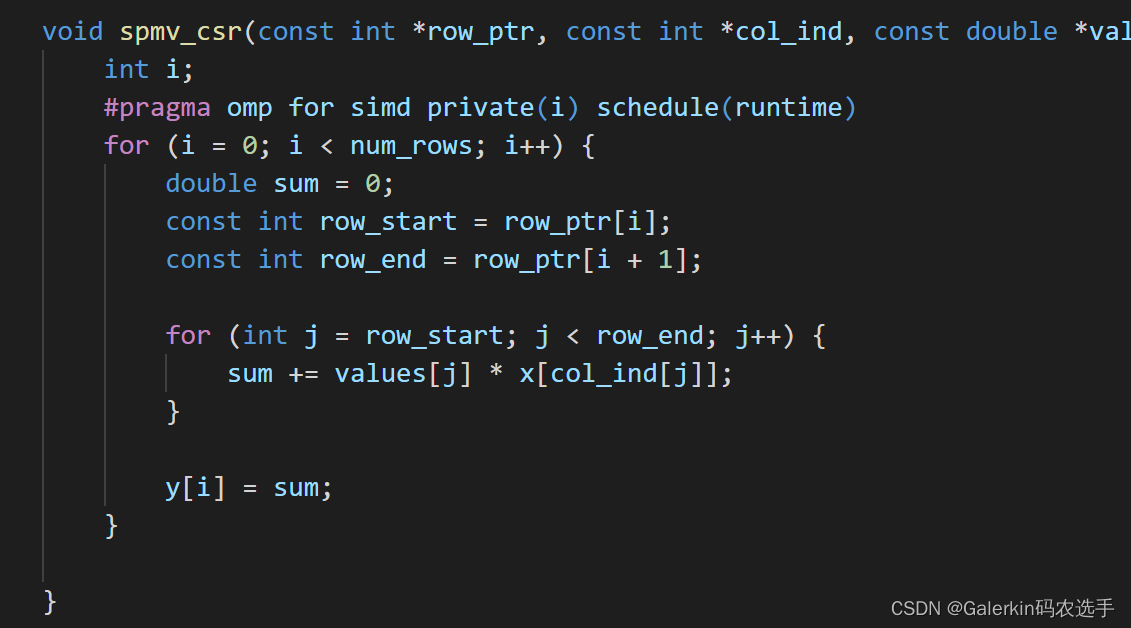
由于稀疏矩阵向量乘法的速度太快，所以为了进一步观察不同并行策略对时间的影响，这里我们希望稀疏矩阵向量乘法可以做500次，每次迭代都根据上一次的结果作为初始x。