稀疏矩阵的乘法算法优化

原创于 2025-03-10 21:03:24 发布 · 540 阅读

7 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #矩阵

C语言专栏收录该内容

149 篇文章

订阅专栏

一、结构体实现非零元三元组

typedef struct{
    int row,col;    //三元组的行号、列号；
    int item;        //三元组的值;
}Triple;

二、稀疏矩阵类实现

class TripleMatrix{
private:
    Triple data[MAX];//非零元三元组
    int mu,nu,num;   //矩阵的行数、列数和非零元个数
public:
    TripleMatrix();
    TripleMatrix(int m,int n);//创建对象时,完成属性的初始化
    ~TripleMatrix();
    Status setItem(int row,int col,int item);//根据行号，列号，非零元，在尾部添加一个三元组项
    int getItem(int row,int col);//根据行号列号，获得矩阵元素值
    void printMatrix();//按矩阵方式打印稀疏矩阵
    void printTriple();//打印三元组数组
    friend bool matrixAdd(TripleMatrix a,TripleMatrix b,TripleMatrix& result);
    friend bool matrixMulty(TripleMatrix a,TripleMatrix b,TripleMatrix &result);
};

三、稀疏矩阵乘法运算实现

一、一般矩阵实现方法

对于一个矩阵，我们要先熟悉它的乘法运算法则，再去进行代码实现。

首先我们要知道一个规则，只有某一矩阵的行数与另一矩阵的列数相等，才可进行计算

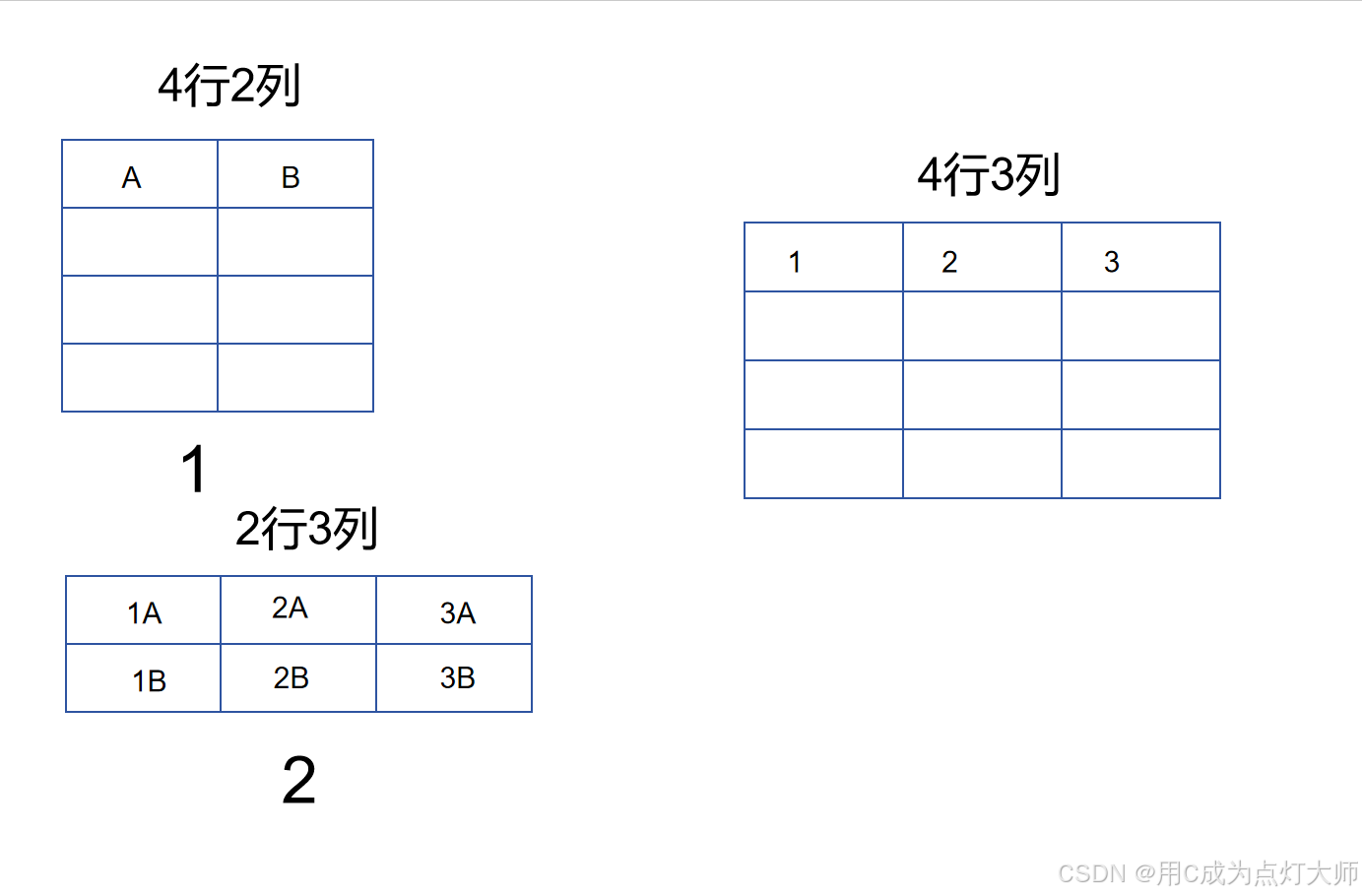
如图，假设一个4行2列的矩阵和一个2行3列的矩阵进行乘法运算，那么将会得到一个4行3列的矩阵，并且结果矩阵中标号为1的元素的运算过程如下：

1 = A * 1A + B * 1B

同理，我们可以得到结果矩阵中标号为2、3元素的运算过程：

2 = A * 2A + B * 2B 3 = A * 3A + B * 3B

那么，我们不难推断结果矩阵的其他元素也是由类似的运算得到的。即结果矩阵x行y列的元素（k）的计算过程为：

k = (1号矩阵第x行第一个元素) * (1号矩阵第y列第一个元素) + (1号矩阵第x行第二个元素) * (1号矩阵第y列第二个元素) + ......

因此，我们可以写出对应的代码

bool matrixMulty(TripleMatrix a,TripleMatrix b,TripleMatrix &result)
{
    if(a.nu != b.mu) return false;    //判断是否满足进行计算的前提条件

    for(int i = 1; i <= a.mu; i ++)  //i表示第一个矩阵的行
    {
    	for(int j = 1; j <= b.nu; j ++)    //j表示第二个矩阵的列
    	{

    		int sum = 0;

    		for(int k = 1; k <= a.nu; k ++)    //k表示第一个矩阵的行和第二个矩阵的列
    		{
    			sum += a.getItem(i, k) * b.getItem(k, j);
			}

			result.setItem(i, j, sum);

		}
	}

	return true;

}

二、稀疏矩阵优化

可以发现，当矩阵中非零元素比较少时，上述算法中的挨个遍历就显得有点多余了，时间复杂度也达到了O(mnk)，我们下面尝试优化。

在稀疏矩阵类中，我们设置了data来存储非零元素，num来表示非零元素的个数，那么，比较简单想到的就是利用data从而避免访问到零元素

bool matrixMulty(TripleMatrix a,TripleMatrix b,TripleMatrix &result)
{
    if(a.nu != b.mu) return false;
    int j = 0;
    Triple tempa, tempb;
    for(int i = 0; i < a.num; i ++)
    {
    	tempa = a.data[i];
    	for(int j = 0; j < b.num; j ++)
    	{
    		tempb = b.data[j];
	    	if(tempa.col == tempb.row)
	    	{
	    		Triple temp;
	    		temp.row = tempa.row;
	    		temp.col = tempb.col;
	    		temp.item = result.getItem(temp.row, temp.col);
	    		temp.item += tempa.item * tempb.item;
	    		result.setItem(temp.row, temp.col, temp.item);
			}
		}
	}
	return true;

}

这样，我们就把复杂度降低到了O(num1 * num2)，其中num1和num2为两个矩阵非零元素的个数。

不过，我们似乎还可以考虑是否可以筛掉a中的某些非零元素，从而在一开始就能减小部分计算量。

bool matrixMulty(TripleMatrix a,TripleMatrix b,TripleMatrix &result)
{
    if(a.nu != b.mu) return false;
    int j = 0;
    Triple tempa, tempb;
    for(int i = 0; i < a.num; i ++)
    {
    	tempa = a.data[i];
    	
    	if(tempa.col < b.data[0].row) continue;
    	if(tempa.col > b.data[b.num - 1].row) continue;
    	
    	for(int j = 0; j < b.num; j ++)
    	{
    		tempb = b.data[j];
	    	if(tempa.col == tempb.row)
	    	{
	    		Triple temp;
	    		temp.row = tempa.row;
	    		temp.col = tempb.col;
	    		temp.item = result.getItem(temp.row, temp.col);
	    		temp.item += tempa.item * tempb.item;
	    		result.setItem(temp.row, temp.col, temp.item);
			}
			if(tempa.col < tempb.row)
			{
				break;
			}
		}
	}
	return true;

}

我们来思考一下矩阵乘法的运算法则，a中的第n行与b中第n列进行运算得到结果，那么，如果a的第n行没有非零元素，b的第n列无论是什么值，得到的结果都会是0，同理，b的第n列没有非零元素时，可以直接跳过a的第n列了。

那么，现在的复杂度肯定是要小于等于O(num1 * num2)了。能不能更进一步？

可以！

bool matrixMulty(TripleMatrix a,TripleMatrix b,TripleMatrix &result)
{
    if(a.nu != b.mu) return false;
    int j = 0, flag = 0;
    Triple tempa, tempb;
    for(int i = 0; i < a.num; i ++)
    {
    	tempa = a.data[i];
    	
    	if(tempa.col < b.data[0].row) continue;
    	if(tempa.col > b.data[b.num - 1].row) continue;
    	if(flag)
    	{
    		for(int j = 1; j <= b.nu; j ++)
    		{
    			tempb.row = tempa.col;
    			tempb.col = j;
    			tempb.item = b.getItem(tempb.row, tempb.col);
    			Triple temp;
    			temp.row = tempa.row;
		    	temp.col = tempb.col;
		    	temp.item = result.getItem(temp.row, temp.col);
		    	temp.item += tempa.item * tempb.item;
		    	result.setItem(temp.row, temp.col, temp.item);
			}
		}
    	else
    	{
    		for(int j = 0; j < b.num; j ++)
	    	{
	    		tempb = b.data[j];
		    	if(tempa.col == tempb.row)
		    	{
		    		Triple temp;
		    		temp.row = tempa.row;
		    		temp.col = tempb.col;
		    		temp.item = result.getItem(temp.row, temp.col);
		    		temp.item += tempa.item * tempb.item;
		    		result.setItem(temp.row, temp.col, temp.item);
				}
				if(tempa.col < tempb.row)
				{
					if(j > b.nu) flag = 1;
					break;
				}
			}
		}
    	
	}
	return true;

}