周期函数的傅立叶变换为什么是由一些冲激函数组成？

周期函数傅立叶级数的频谱幅值是有限值，但是为什么它的傅立叶级数就成了一些冲激函数组成的呢？为什么表示频谱密度就是冲激函数了呢？

sieben

EE

傅里叶变换得到的是频率密度函数，它的纵坐标是幅值密度。

而傅里叶级数的纵坐标是真实的幅值。

首先题主有笔误，不是“傅里叶级数成了由一些冲激函数组成”，应该是“傅里叶变换由冲激函数组成”。

什么意思呢？对于傅里叶变换后的频谱，纵坐标的单位是“信号量纲/Hz”，表示频率w处的幅值密度是F(w)，而不是说他的幅值是F(w)。所以谈论单个点的幅值是没有意义的。

这就跟概率密度和分布函数的概念一样。拿一个点投射到区间在(0,1)的线段上的概率来举例，这是一个均匀分布。概率密度是1，但这不代表投到区间(0,1)之间任意一点的概率是1，而是指投到dx的微小区间的概率是1*dx。傅里叶变换得到的函数就类似于概率密度函数。

而周期信号的傅里叶级数的纵坐标，才是对应的真是幅值。类似于分布函数。

综上所述，周期函数的傅里叶变换为什么是由冲激函数组成就好理解了。就拿最简单的余弦函数f(t)=cos(w1t)的傅里叶变换频谱来说，

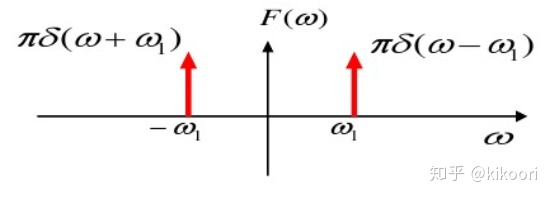
可以看到存在正、负两个频率，其对应的频率密度为pi倍的冲激函数幅值。

首先说下负频率（注意不是“复频率”）代表什么。任何函数进行傅里叶变换都会有一个负数的频率(其实复指数形式的傅立叶级数展开，也会得到负频率，其来源相同)，其来源就是来自于欧拉变换，即

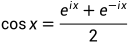
由于现实世界没有负数频率，所以用复数 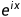来进行傅里叶变换的运算，一定会产生一对正、负频率，这样在还原成实信号（也就是我们现实世界的信号）时，由于正、负频率的虚部是共轭的，所以可以抵消掉，就只剩实部的信号，也就是现实中的信号。(这一段对知识的理解有误，数学的解释有很多资料可以参考，但我不知道该如何去定性的解释才能比较好说明白，故仍做保留。但我想说一下，从公式来看，Fourier正变换有点像是用一个e^(-jwt)的函数去提取时域函数f(t)里的频率成分，提取的原理就是三角函数的正交性，只有频率相同的信号积分出来才不等于0，才具有幅值跟相位，然后在以w为横轴的座标系上排列，得到的就是频域了；相应地，Fourier反变换就是在频域里用e^(jwt)去整合频域的信息，一个特定频率w的e^(jwt)信号就是一个该频率下正、余弦函数的组合，那么把所有频率的信号与e^(jwt)相乘就是改变了其幅值与相位，再把这些修正了的e^(jwt)相加，得到的就是原时域信号，类似一个频域轴被无限细分版本的Fourier级数，而不是限定在基波，一次谐波，二次谐波等等这些离散的频率上，2019/12/22)

解释完了负频率的来源后，再来看幅值密度。只有在w1（-w1）这一点的幅值密度大小为冲激函数的幅值，对它进行积分后，幅值才是一个有限值。如果在这里理解为傅里叶级数频谱里的幅值，那么积分后，信号幅值就变为零了，这显然是不符合实际的。也就是说，w1这一点及其周围极小范围dx的邻域内，幅值密度是冲激函数。也就是说这个余弦函数只有一个频率点有幅值跟相位。

至于为什么提到积分？因为真实信号就是将频谱里每一个频率下的幅值密度与复指数相乘后再求积分（也就是傅里叶变换的逆变换）。这就像分布函数一般是我们真正想知道的，所以要对概率密度函数求积分。

1：拿单位冲击函数的傅立叶变换来说更容易理解傅立叶变换。单位冲激函数的傅立叶变换频谱是一条值为1的平行线。说明其频谱幅值密度处处相等，且等于1。那我们在整个频域内从频率的负无穷积分到正无穷，虚部因为共轭抵消后，那剩下的不就只有趋于无穷的实部了，即冲激函数。所以单位冲激函数有一个很好的特性，幅值频谱密度为1，说明任何一个频率点的幅值密度是一样的且为单位1，这样的好特性可以拿来观察系统的响应。特别是对于线性非时变系统，只要得到单位冲激响应，其余类型输入信号的响应就在单位冲激响应上做线性运算就可以了。

2：其实从正(余)弦函数的傅立叶变换的推导的几个方法来看，其中一种就是先加矩形窗，得到只有几个周期的正弦函数的傅立叶变换，其由抽样函数(Sa)构成。然后再将矩形窗推广至正弦函数的整个时域，而在频域内Sa函数就会收敛到冲激函数。可以看到，对于加矩形窗的正弦函数，是非周期的，频谱幅值密度是有限值，频率非常分散，分散至整个频域(Sa函数)。而当矩形窗在时域逐渐扩展到整个时间时，频率就逐渐收敛到正弦函数的频率，且幅值密度逐渐变高直至趋于无穷。所以综合展开1，我们越想知道频域由哪些分量构成，时域就越难以观察全；若我们越想看到时域的全貌，那频域就会非常集中而难以观察。感觉有些像海森堡原理？

---

还有“频谱”这个概念，要区分是傅立叶级数的频谱还是傅立叶变换的频谱。其中傅立叶级数的频谱，还分为用复指数变换的频谱，和用三角函数变换的频谱，前者包含负频率部分，后者则不存在负频率部分，因为三角函数形式的傅立叶级数，本就是一串实信号的求和，这也就是我们最容易理解的“方波信号就是直流信号和一系列正(余)弦信号的叠加”。

转载：https://www.zhihu.com/question/22147488?utm_id=0

周期函数的傅里叶变换为什么是由一些冲激函数组成？