如何理解离散傅里叶变换DFT----实验数据说话

转载：知乎 牙非涯 南京理工大学 计算机博士在读

https://zhuanlan.zhihu.com/p/459765153?utm_id=0

在 上一篇文章中， 离散时间傅里叶变换迈出了将傅里叶变换变成实用工具的第一步。我们将在这篇文章中详细介绍的 离散傅里叶变换(DFT) 将完成这一旅程，并为我们提供一个我们可以实际实现的算法。

1. 三 个无穷大

正如DTFT那篇文章中提到的那样，傅里叶变换的问题在于它假设我们可以处理无限的事物。这显然是不可能的，我们所能接触到的都是有限的

傅里叶变换假设我们可以在无穷时间线上获得信号。

假设以测试可能存在的每一个频率，无限数量的频率。

假设在每个连续时间点，都可以测到信号

DTFT 通过对信号进行采样，设法摆脱了无穷大 3。现在 DFT 也将摆脱 1 和 2 的无穷大。

FT，DTFT 和 DFT 的公式

FT，DTFT 和 DFT 的公式比较

其中n 是离散时间值的索引 ，其与时间t之间关系为: ，
（推导： ⇑ ×n=t, N=信号持续时间×R⇑ ）
k 是离散频率值的索引, 其与频率 f 之间关系为：f= R , （推导：自己推）
N 是测量信号的总点数
R 是采样率，每秒测量信号的点数

与 DTFT 一样，离散傅里叶变换将时间视为离散的，并且 x(n) 的离散项都使用求和符号 Σ 加在一起。但是，对于频率项，在 DFT 中频率 f 也是离散的，频率 f 在 DFT 中被有限项替换 (推导： )，我们只测试某些特定的频率，而且测试的范围只能是0~ R，为减少离散造成的信号的丢失，在频域上两个相邻频率之间的步长最小，即频率分辨率设为 ；为测试最多的频率，所以k取值为k=0,1,2,3,….,N−1

更新：这里k最大值为什么取N-1

对于一段连续信号x(i)，以采样频率为R，采集N个样本点，得到一段离散信号x(n), 分析这段离散信号，其频率分辨率最小为 R/N ，即频率小于这个值的信号信息将被丢失（无法分析），至于为什么？

假定对于一段连续信号存在1Hz/s和0.5Hz/s的信号，将其离散化，采样频率为4Hz/s，采样时长1s，即4个样本点，下图红线左侧为此处采样的结果。(手绘就不拟合曲线了)

此时最小频率分辨率为 4/4=1Hz/s , 对于频率为1Hz/s的信号(图中紫色)，本次采样恰好采集一个完整的周期，而对于频率为0.5Hz/s的信号(图中黄色)，本次采样只获取到周期的一半信号，其他部分丢失

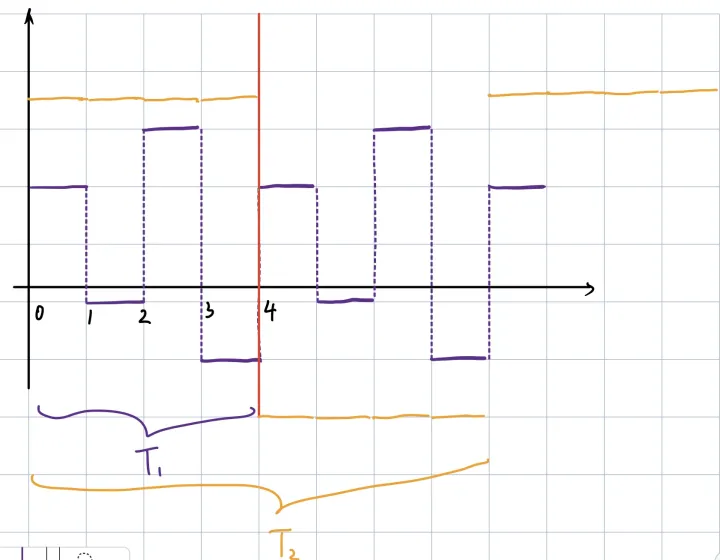
因此，要尽可能的拟合真实连续信号，需要增大采样率以涵盖信号中的最高频率，增加采样样本点数以涵盖信号中的最低频率。

---

2. DFT 中的频率分辨率

为了将傅里叶变换转换为 DFT，我们必须做出一些妥协，信号必须是离散的。换句话说，我们必须放弃信号中可用的一些信息

采样信号

在 DTFT 中，我们仅在某些离散时间点对信号进行采样或测量。现在在 DFT 中，我们也只针对某些离散频率测试信号。这意味着我们将不得不放弃信号中可用的一些频率信息。理想情况下，我们只想放弃我们绝对需要的尽可能多的信息。换句话说，考虑到系统的处理和时间限制，我们希望 DFT 的频率分辨率尽可能大。两个相邻频率之间的步长大小反应了我们频率分辨率。

低频分辨率/频率之间的大步长

高频率分辨率/频率之间的小步长

3. 采样率和混叠

如果我们对上面的离散采样信号执行DFT，将得到如下图所示的频域图。

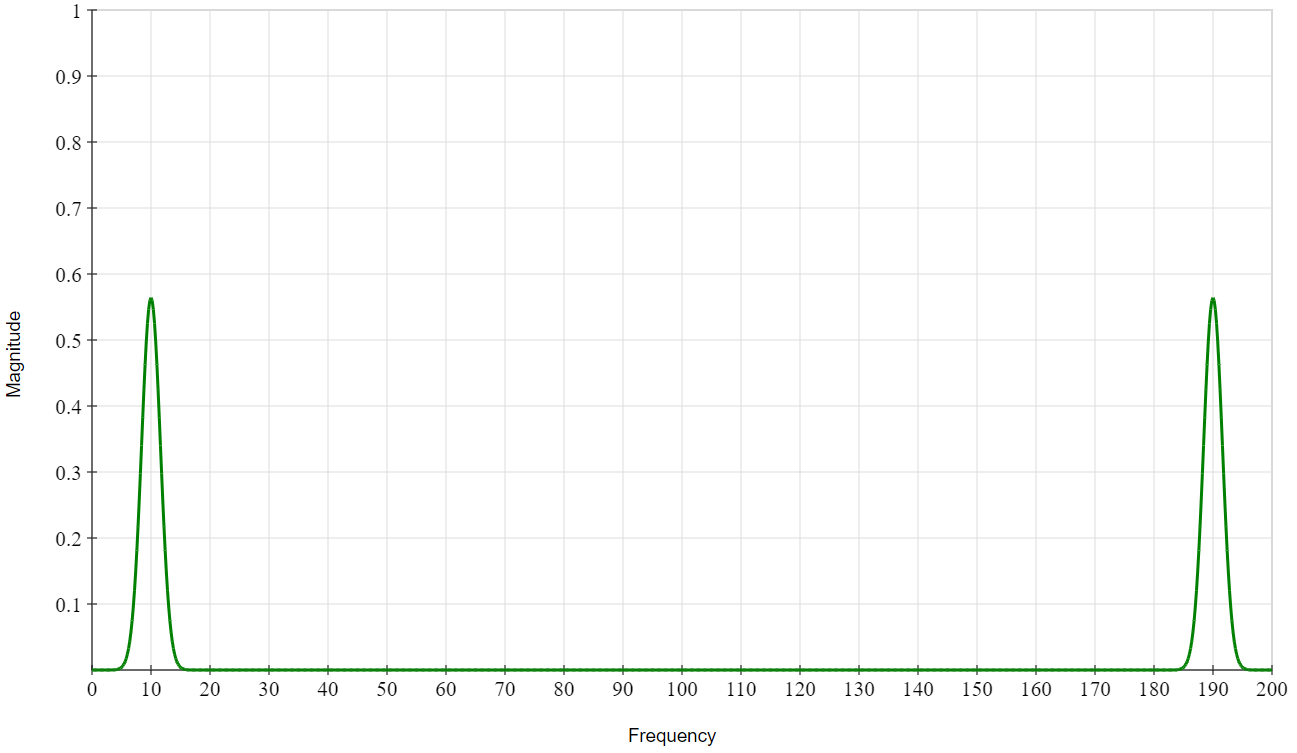
采样信号的重复频谱

这个信号不仅包含一组 10Hz 左右的频率，还有一个在 190Hz 左右。事实上，更高频率的波峰甚至更多，只是，DFT 不会测试高于采样频率的频率。我们称这些是鬼频率，根本不存在于信号中，而是一种数学上的问题。它们的出现是因为我们掌握的有关信号的信息存在空白。信号被采样，这意味着它仅在某些时间点定义。因此，只要较高频率的正弦波在信号定义的那些时间点达到正确的值，那么 DTFT 和 DFT 都会认为这些频率存在于信号中，就像这样：

离散信号放大后

在对信号进行采样时，若不想丢失太多信息，则必须以至少两倍于信号中最高频率的频率对其进行采样。例如对于语音信息，需要每秒至少对声音信号进行 40,000 次（40kHz）采样，这是因为我们的耳朵可以检测到的最高频率是 20kHz。

回到上面的 DFT 产生的频率图，这次我在 100Hz 处画了一条黑线，被称为奈奎斯特频率的对称就点位于黑线所在的 100Hz 处。至于奈奎斯特频率后续可以专门出一篇文章来讲，另外还有混叠，随着降低采样频率，每秒测量信号的次数越来越少。因此，我们正在丢失越来越多的信号的信息。奈奎斯特频率始终是采样频率的一半，它越来越接近信号中的最高频率。在大约 30Hz 的采样率下，奈奎斯特频率会碰到 10Hz 的频率组，我们从信号中丢失了太多信息。结果，信号开始失真。这种失真称为混叠。

混叠

---

4. 计算 DFT

使用 DFT 找出构成以下时域信号的正弦波的特性：

时域连续信号x(t)

这个信号是我们人工合成的，事先知道存在10Hz频率的信号，现在我们需要做的第一件事是通过采样将此信号转换为离散时间信号。首先对其采样 200 次： N =200，该信号持续 1 秒，因此我们的采样率为： R =200Hz/s

离散时域信号x(n)

DFT算法步骤

现在以k=5为例，即频率为 5*200/200，来看这个频率的余弦分量如何计算：

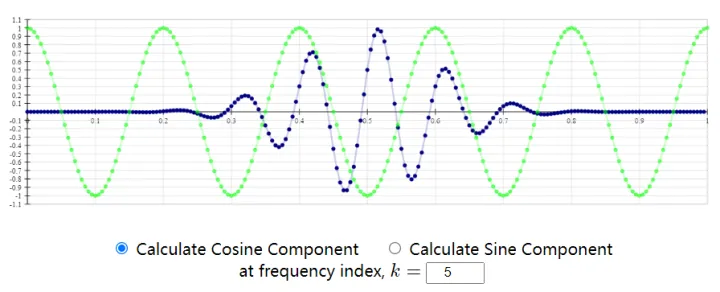
绿线为5Hz的测试余弦，

离散信号点与5Hz的测试余弦对应点相乘，再求和就得到该频率下的余弦分量，具体结果如下：

5Hz的余弦分量

5. 振幅和相位

余弦分量结果称为实部，ℜ，正弦分量结果称为虚部，ℑ。完成所有k值的计算结果后，再计算对应幅度与相位

幅度：M(k)=ℜ(k)2+ℑ(k)2 相位： P(k)=tan−1(ℑ(k)ℜ(k))

所有k值对应的结果

所以现在我们已经使用离散傅里叶变换来提取真实采样信号的频率、幅度和相位信息。但是，仍然面临一个问题。这个合成的信号非常适合我选择的块大小。它在块开始时为零，并在块结束之前也趋于零。然而，并不是所有的信号都那么周到。大多数时候，由于各种实际限制，我们被迫选择比信号更短的块大小。

如果信号在块的开头或结尾不为零会发生什么？

这将导致称为频谱泄漏的问题。一个我们无法完全解决的问题，但可以使用一种称为加窗的方法来减少它。