hello， 小伙伴们，我们继续进行傅里叶变换的讲解，更多有关傅里叶变换的公式原理、公式推导及代码实现等，可在作者主页下的视频或文章列表中找到。
本文讲解离散傅里叶变换的公式推导及代码实现，同时理解本文需要一定的傅里叶相关基础知识，为了更好的理解本文，建议你先阅读以下文章。
AI工作室：彻底搞懂傅里叶变换之实用干货分享(一)-从原理到实战文章汇总21 赞同 · 1 评论文章
AI工作室：彻底搞懂傅里叶变换之实用干货分享(二)-傅里叶级数38 赞同 · 6 评论文章
AI工作室：彻底搞懂傅里叶变换之实用干货分享(三)-傅里叶变换基础14 赞同 · 2 评论文章
1.复数形式傅里叶变换与逆变换
傅里叶变换一般指的是连续傅里叶变换，其定义如下:
傅里叶逆变换的定义如下:
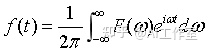
有了傅里叶变换了，为什么还要搞出个离散傅里叶变换呢？我们从上面公式可以看出，不管是傅里叶变换还是逆变换都是正负无穷的连续积分，这在数学公式上尚可以根据微分及极限求解公式进行计算，但却不太方便在计算机上实现，因为计算机是一个离散系统，那离散傅里叶变换就是用来解决这个问题的，使用计算机这个离散系统进行有限近似计算。不过在讲离散傅里叶变换之前，先说说离散时间傅里叶变换(DTFT)。
2.离散时间傅里叶变换(DTFT)
在离散系统中，假如x(t)为连续系统信号，要转换成离散系统，就要先进行采样，采样频率为 fs ，采样点时间间隔为 Ts=1fs ,冲击采样序列为:
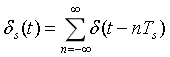
则取样之后的信号为
这里t如果取的不是 Ts 的整数倍，其值没有定义，即只能取 Ts 的整数倍。
连续信号的傅里叶变换的定义为
则采样后的信号傅里叶变换为
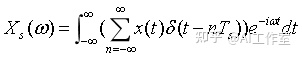
交换一下积分与求和顺序
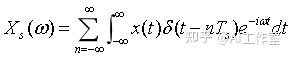
由 δ(t) 的筛选性
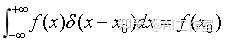
得
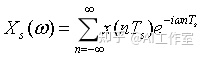
对数字系统而言，我们只有x(t)采样后的信号{x[n]}，注意，它是一个序列，第n个采样发生在时间t=nTs，因此，可将连续信号的傅里叶变换写成如下形式:
上式称为离散时间傅里叶变换(Discrete Time Fourier Transform)，简称DTFT，也就是无限长离散信号如何进行傅里叶变换。
3.离散傅里叶变换(DFT)与逆变换(IDFT)
离散时间傅里叶变换中原始信号还是无限长的，即使采样后，采样点也是无限个，可以认为周期为无限长，因此它的频谱就趋向于连续，而连续的频谱同样不利于计算机处理，所以频率也要离散化才行，所需要的技术就是离散傅里叶变换DFT(Discrete Fourier Transform)，即具有周期特性离散信号的傅里叶级数(就是将无限长的离散信号进行截短至N个采样点，然后将这个N个采样点进行周期延拓，变成周期信号，这样其频率就离散了)。
离散傅里叶变换与连续傅里叶变换“类似”，只不过把积分换成级数，DFT以及IDFT的定义如下:
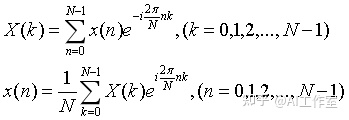
下面进行详细推导。
我们知道，周期函数可以用傅里叶级数展开，在引入 δ(t) 函数后，更一般的周期函数也能被展开了，因为可以使用 δ(t) 函数进行采样，变成有限长离散序列，可以看成是周期信号。
根据连续信号x(t)按照采样时间Ts进行抽样N次δ(t−nTs)，并将这N个数值进行周期延拓，可以得到周期的离散信号x[n]，其周期T=N*Ts，频率为f=2pi/T，在一个周期T内，其共表达式为
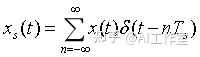
令
可以获得离散周期信号的傅里叶级数为
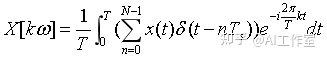
由δ(t)函数的筛选性，有
令
得
这就是离散周期信号的傅里叶变换，理论上离散周期信号的频谱是有无穷多的，但是由于 e−i2πNkn 的周期性(将其展开成三角函数后sin和cos)，一般我们只取主值区间0<=k<N-1进行研究。
上面我们计算了离散周期信号的频谱，即不同频率分量下对应的系数，下面将得出一个重要的结论
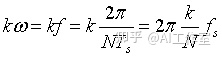
也就是说
离散周期傅里叶变换后第k个数对应的频率是 kNfs
同时，离散周期傅里叶变换后，计算出来的是一个复数形式，即用正弦和余弦组合的形式近似表示原始信号，所以幅值应该是两者的组合，sqrt(A_sin^2 + A_cos^2)。
4.离散傅里叶变换的物理意义
采样定理：采样频率大于信号中最高频率的2倍时，采样后的数字信号可以完整地恢复出原始信号。一般实际应用中保证采样频率为信号最高频率的2.56~4倍。
假设信号频率为F，采样频率为Fs，采样点数为N。为了方便进行DFT运算，通常N取2的整数次幂。
N个采样点，经过DFT变换后的结果为N个复数，每个复数对应一个频率(第n<=N/2个点对应的频率为(n-1)/N*Fs)，该复数的模值表示该频率的振幅特征。怎么去理解这段话呢，还要从信号的傅里叶级数复数形式说起，对于时域信号f(t)，其傅里叶级数展开为
其中
在离散傅里叶中，n不是取无穷个，而是N个，于是有
其中
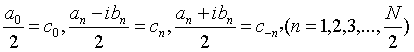
可以看到，原始时域信号f(t)经DFT后，DFT的结果其实是原始信号傅里叶展开的个项系数，c0为常数项，cn是不同频率的正余弦系数。
该振幅特征和原始信号的振幅之间的关系是：如果原始信号的振幅为A，则DFT结果的每个点(除了第一个直流分量点)的模值就是A的N/2倍；而第一个点的模值是直流分量振幅的N倍。同时，这N个复数点去掉第一个点(直流分量)后剩下的N-1个点是关于其中心共轭对称的，因此实际只需要取前一半点的频谱即可，因为共轭对称的两个点的模值(振幅)相同。
##注意，以上结论是针对numpy的fft运算结果总结的，在numpy.fft中没有进行1/N归一化处理，而上面推导中都是除N的，即
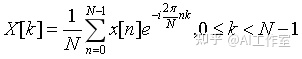
5.实验验证
上面列了一些公式，比较抽象，下面我们根据公式，使用python编写程序进行验证。
这里我们定义一个时域信号
y=2+3cos(2π×50t)+1.5cos(2π×75t)
不难求出其包含一个50hz和一个75hz的频率信号。
下面使用256hz的采样频率，对信号进行离散化，得到x[n]，然后先做离散傅里叶变换，分析其频谱，再做逆傅里叶变换，还原回原时域信号。同时，为了验证计算的正确性，在程序里分别使用np.fft模块，同时再根据离散傅里叶变换公式分别作了计算，并进行对比。
#! /usr/bin/python3
# -*- encoding:utf-8 -*-
import matplotlib.pyplot as plt
from matplotlib.pylab import mpl
import numpy as np
from numpy import pi, cos, sin
# 中文显示问题
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
def test2():
'''
离散傅里叶变换
一维时序信号y，它由2V的直流分量(0Hz)，和振幅为3V，频率为50Hz的交流信号，以及振幅为1.5V，频率为75Hz的交流信号组成：
y = 2 + 3*np.cos(2*np.pi*50*t) + 1.5*np.cos(2*np.pi*75*t)
然后我们采用256Hz的采样频率，总共采样256个点。
'''
fs = 256 # 采样频率， 要大于信号频率的两倍
t = np.arange(0, 1, 1.0 / fs) # 1秒采样fs个点
N = len(t)
freq = np.arange(N) # 频率counter
# x = 2 + 3 * cos(2 * pi * 50 * t) + 1.5 * cos(2 * pi * 75 * t) # 离散化后的x[n]
x = 2 + 3 * cos(2 * pi * 10 * t) + 1.5 * cos(2 * pi * 15 * t) # 离散化后的x[n]
X = np.fft.fft(x) # 离散傅里叶变换
'''
根据STFT公式原理，实现的STFT计算，做了/N的标准化
'''
X2 = np.zeros(N, dtype=np.complex) # X[n]
for k in range(0, N): # 0,1,2,...,N-1
for n in range(0, N): # 0,1,2,...,N-1
# X[k] = X[k] + x[n] * np.exp(-2j * pi * k * n / N)
X2[k] = X2[k] + (1 / N) * x[n] * np.exp(-2j * pi * k * n / N)
fig, ax = plt.subplots(5, 1, figsize=(12, 12))
# 绘制原始时域图像
ax[0].plot(t, x, label='原始时域信号')
ax[0].set_xlabel('Time (s)')
ax[0].set_ylabel('Amplitude')
ax[1].plot(freq, abs(X), 'r', label='调用np.fft库计算结果')
ax[1].set_xlabel('Freq (Hz)')
ax[1].set_ylabel('Amplitude')
ax[1].legend()
ax[2].plot(freq, abs(X2), 'r', label='根据STFT计算结果')
ax[2].set_xlabel('Freq (Hz)')
ax[2].set_ylabel('Amplitude')
ax[2].legend()
X_norm = X / (N / 2) # 换算成实际的振幅
X_norm[0] = X_norm[0] / 2
ax[3].plot(freq, abs(X_norm), 'r', label='转换为原始信号振幅')
ax[3].set_xlabel('Freq (Hz)')
ax[3].set_ylabel('Amplitude')
ax[3].set_yticks(np.arange(0, 3))
ax[3].legend()
freq_half = freq[range(int(N / 2))] # 前一半频率
X_half = X_norm[range(int(N / 2))]
ax[4].plot(freq_half, abs(X_half), 'b', label='前N/2个频率')
ax[4].set_xlabel('Freq (Hz)')
ax[4].set_ylabel('Amplitude')
ax[4].set_yticks(np.arange(0, 3))
ax[4].legend()
plt.show()
test2()
程序输出结果如下，可以看出，不管使用推导公式还是调用库，其计算结果都是正确的。
转载：
anders 南京航空航天大学 机械电子硕士
扫一扫
1763
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
