数字图像频谱的中心化

研究数字图像有时需要变换到频率做处理，比如滤波等。

但直接对数字图像进行二维DFT变换得到的频谱图是高频在中间，低频在四角，为了把能量集中起来便于使用滤波器，可以利用二维DFT的平移性质对频谱进行中心化。

（1）原理

所以推导出来的结论是——对数字图像的每个像素点的取值直接乘以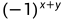就行，x和y是像素坐标。

频谱图比较亮的地方就是低频，因为图像的能量一般都是集中在低频部分。

频谱中心化以后，就是低频在中间高频在四周了。

频谱的最中间（u=v=0）就是频率变化最慢的分量，是图像频谱的直流分量，它的值是原图的平均灰度级。

（2）频域滤波

（3）一个有趣的应用

上图下面的左1是F(0,0)，即平均灰度级。

左2是频谱减去左1后，以直径为25的圆环截取圆环内低频分量，反变换得到的图像。

后面是圆环直径依次增大，不断截取更多高频成分后，反变换得到的图像。

可见：

高频是细节信息，低频代表的概貌信息。

减去平均灰度级以后，反变换得到的图像的灰度在0左右，图像比较暗

————————————————

版权声明：本文为优快云博主「doubleslow;」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。

原文链接：https://blog.youkuaiyun.com/qq_36607894/article/details/92809731