数据结构习题集作业代码（第一章）

1.16-三整数排序

Description
写一个算法，自大到小依次输出顺序读入的三个整数，x，y和z的值
Input
输入x，y和z
Output
输出自大到小的排序

#include<stdio.h>
void swap(int *x,int *y){
    int t=*x;
    *x=*y;
    *y=t;
}
int main(){
    int x,y,z;
    scanf("%d%d%d",&x,&y,&z);
    if(x<y)swap(&x,&y);
    if(y<z)swap(&y,&z);
    if(x<y)swap(&x,&y);
    printf("%d %d %d",x,y,z);
    return 0;
}

1.17-k阶斐波那契数列

Description
已知k阶斐波那契序列的定义为

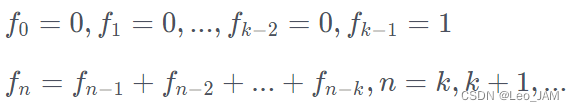
试编写求k阶裴波那契序列的第m项值的函数算法，k和m均以值调用的形式在函数参数表中出现。
Input
输入为k和m（m从0开始，$f_0$ 对应m=0）
Output
输出第m项的值

#include<stdio.h>
/*int a[100][100],b[100][100],c[100][100],k,m;
void copy(int (*a)[100],int (*b)[100]);
void operate(int (*a)[100],int (*b)[100]){
    int i,j,l;
    int c[100][100];
    for(i=1;i<=k;++i){
        for(j=1;j<=k;++j){
            c[i][j]=0;
        }
    }
    for(i=1;i<=k;++i){
        for(j=1;j<=k;++j){
            for(l=1;l<=k;++l){
                c[i][j]+=a[i][l]*b[l][j];
            }
        }
    }
    copy(a,c);
}
void init(int (*a)[100]){
    int i,j;
    for(i=1;i<=k;++i){
        for(j=1;j<=k;++j){
            a[i][j]=0;
        }
    }
}
void copy(int (*a)[100],int (*b)[100]){
    int i,j;
    for(i=1;i<=k;++i){
        for(j=1;j<=k;++j){
            a[i][j]=b[i][j];
        }
    }
}
void power(int (*a)[100],int k){
    int tmp[100][100],i;
    init(tmp);
    for(i=1;i<=k;++i){
        tmp[i][i]=1;
    }
    while(k){
        if(k&1){
            operate(tmp,a);
        }
        operate(a,a);
        k>>=1;
    }
    copy(a,tmp);
}
int main(){
    scanf("%d%d",&k,&m);
    if(m<k){
        printf("0");
        return 0;
    }
    else{
        if(k==m){
            printf("1");
            return 0;
        }
    }
    init(a);
    a[1][k]=1;
    init(b);
    int i;
    for(i=1;i<=k-1;++i){
        b[i+1][i]=1;
    }
    for(i=1;i<=k;++i){
        b[i][k]=1;
    }
    power(b,m-k+1);
    operate(a,b);
    printf("%d",a[1][k]);
    return 0;
}*/
int a[100000]={},m,i,j,k;
int main(){
	scanf("%d%d",&k,&m);
	a[k-1]=1;
	for(i=k;i<=m;++i){
		for(j=i-k;j<i;++j){
			a[i]+=a[j]; 
		}
	}
	printf("%d",a[m]);
}

1.18-田径对抗赛

Description

假设有A,B,C,D,E 五个高等院校进行田径对抗赛，各院校的单项成绩均已存入计算机，并构成一张表，表中每一行的形式为

项目名称 - 性别 - 校名 - 成绩

编写算法，处理上述表格，以统计个院校的男、女总分和团体总分，并输出

Input
输入包含多行，每行代表表格中的一行，每个字段以空格分隔

M代表男生，F代表女生

Output
输出每个学校的男，女总分和团体总分，按如下顺序

第一行输出学校A的男生总分

第二行输出学校A的女生总分

第三行输出学校A的团体总分

第四行输出学校B的男生总分

…

如果某个学校没有男生或女生，则跳过对应的行数（如学校A没有女生，则跳过第二行）

#include<stdio.h>
#include<stdlib.h>
#include<string.h>
char p,g,s;
int score,i;
int vis[5];
int S[6][3];
int main(){
	while(scanf("%c ",&p)!=EOF){
		scanf("%c %c %d\n",&g,&s,&score);
		vis[s-'A']=1;
		if(g=='M'){
			S[s-'A'][0]+=score;
		}
		else S[s-'A'][1]+=score;
	}
	for(i=0;i<5;++i){
		if(S[i][0]+S[i][1]==0)continue;
		if(S[i][0]!=0){
			printf("%c M %d\n",i+'A',S[i][0]);
		}
		if(S[i][1]!=0){
			printf("%c F %d\n",i+'A',S[i][1]);
		}
		printf("%c %d\n",i+'A',S[i][0]+S[i][1]);
	}
	return 0;
}

1.20-求一元多项式的值

Description

编写算法求一元多项式$P_n(x_0)={\sum }_{i=0}^n{a}_i{x}_0^i$
​
的值$P_n(x_0)$

Input
输入第一行为$x_0$和n，以空格分隔，$n>=0$
输入第二行为$a_i(i=0,1,...,n),-1000<=a_i<=1000$以空格分隔

Output
输出$P_n(x_0)$的值

#include<stdio.h>
int Quick_Power(int x,int k){
	int ret=1;
	while(k){
		if(k&1){
			ret=ret*x;
		}
		x=x*x;
		k>>=1;
	}
	return ret;
}
int x0,n,i,sum=0;
int main(){
	scanf("%d%d",&x0,&n);
	for(i=0;i<=n;++i){
		int a;
		scanf("%d",&a);
		sum+=a*Quick_Power(x0,i);
	}
	printf("%d",sum);
	return 0;
}