日拱一卒之最小二乘法

日拱一卒之最小二乘法

由于最小二乘法在最近出现的频率比较高，所以单独拎出来研究研究，b站上有个几何的解读，虽然感觉弄得不错，但是还是觉得有点深了，而且有点快，各种公式的嵌套看的有点乱，于是乎，记录下自己的一些理解与看到的东西。

定义

• “二乘” ：在古汉语和数学术语中，“二乘”就是平方的意思。
• “最小” ：指的是我们要让某个数值达到最小。

一句话定义：
最小二乘法是一种数学优化技术，它通过最小化误差的平方和，来寻找数据的最佳函数匹配。
假设你在纸上画了很多个散点，现在你想画一条直线穿过它们，要求这条直线能最能代表这些点的趋势。你怎么确定哪条线是“最好”的？最小二乘法告诉你：那条让所有点到直线的垂直距离的平方加起来最小的线，就是最好的线。

假设有一组真实数据 $y$ 和模型的预测数据 $\hat{y}$。我们希望它们越接近越好。（人工智能方向的理解）

定义“误差”： 我们定义每一个点的误差为 $e_i=y_i-{\hat{y}}_i$（真实值 - 预测值）。

如果直接求和 $\sum (y_i-{\hat{y}}_i)$，会出问题。因为误差有正有负（有的点在直线上方，有的在下方）。正负相抵后，总和可能为 0，但这并不代表直线完美穿过了所有点，可能只是误差刚好抵消了。

去符号： 为了消除符号影响，我们有两种选择：

1. 取绝对值：$|y_i-{\hat{y}}_i|$
2. 取平方：$(y_i-{\hat{y}}_i{)}^2$

为什么选择“平方”而不是“绝对值”？ 这就是最小二乘法的核心智慧，主要有三个原因：

1. 惩罚大误差（关键点） ：

   平方会对大的误差进行“严厉惩罚”。如果误差是 2，平方后是 4；如果误差是 10，平方后变成了 100。

   这意味着，最小二乘法绝不容忍极端偏差。它会拼命把那条线往离得最远的那个点拉一拉，尽量照顾所有点，不让任何一个点掉队太远。

2. 计算方便（求导） ：

   绝对值函数 $|x|$ 在 $x=0$ 处有一个尖角，不可导，数学处理很麻烦。

3. 平方函数 $x^2$ 是光滑的抛物线，处处可导。可以直接求导并令其为 0，一步就能算出答案（解析解）。

4. 统计学背景（高斯分布） ：

   如果假设数据的噪声服从正态分布（高斯分布） ，那么“最小二乘法”求解出来的结果，等价于“极大似然估计”。这意味着它是统计学上最合理的估计。（这个后边再专门研究）

‍

代数推导

第一步：定义损失函数

假设模型为 $Y\approx X\theta$。我们要最小化误差向量 $e=Y-X\theta$ 的模长平方（即能量）：

$$J(\theta )=\Vert Y-X\theta {\Vert }^2$$

写成矩阵乘法形式（实数域）：

$$J(\theta )=(Y-X\theta {)}^T(Y-X\theta )$$

第二步：展开公式

利用矩阵转置规则 $(A-B{)}^T=A^T-B^T$ 和 $(AB{)}^T=B^T{A}^T$：

$$J(\theta )=(Y^T-{\theta }^T{X}^T)(Y-X\theta )$$

$$J(\theta )=Y^{T}Y-Y^{T}X\theta -{\theta }^T{X}^{T}Y+{\theta }^T{X}^{T}X\theta$$

关键技巧：中间两项是标量（实数）。

• $Y^{T}X\theta$ 是一个 $1\times 1$ 的数。
• ${\theta }^T{X}^{T}Y$ 也是一个 $1\times 1$ 的数。
• 标量的转置等于它自己，所以这两项是相等的。

$$J(\theta )=Y^{T}Y-2{\theta }^T{X}^{T}Y+{\theta }^T{X}^{T}X\theta$$

第三步：求梯度（对 $\theta$ 求导）

我们需要用到两个矩阵求导公式：

1. $\frac{\partial ({\theta }^{T}A)}{\partial \theta }=A$ （针对线性项）
2. $\frac{\partial ({\theta }^{T}A\theta )}{\partial \theta }=2A\theta$ （针对二次项，当 $A$ 对称时）

对 $J(\theta )$ 求导：

• $Y^{T}Y$ 对 $\theta$ 是常数 $\to 0$。
• $-2{\theta }^T{X}^{T}Y$ 对 $\theta$ 求导 $\to -2X^{T}Y$。
• ${\theta }^T(X^{T}X)\theta$ 对 $\theta$ 求导 $\to 2(X^{T}X)\theta$。

$${\nabla }_{\theta }J(\theta )=-2X^{T}Y+2X^{T}X\theta$$

第四步：令导数为 0（极值点）

为了找到最小值，令梯度为 0：

$$2X^{T}X\theta -2X^{T}Y=0$$

$$X^{T}X\theta =X^{T}Y$$

这就是著名的“正规方程” (Normal Equation)。

最后左乘逆矩阵 $(X^{T}X{)}^{-1}$：

$$\theta =(X^{T}X{)}^{-1}{X}^{T}Y$$

几何推导：正交投影 (The Geometric Way)

核心思想

1. 列空间：矩阵 $X$ 的列向量张成了一个子空间（平面），记为 $Col(X)$。
2. 限制：无论 $\theta$ 怎么取，$X\theta$ 只能在这个平面上移动。
3. 目标：真实值 $Y$ 通常不在这个平面上（因为有噪声）。我们要在这个平面上找一个点 $\hat{Y}=X\theta$，离 $Y$ 最近。
4. 结论：几何学告诉我们，最近的点就是 $Y$ 在平面上的正交投影。

推导过程

这意味着，误差向量 $e=Y-X\theta$ 必须垂直（正交） 于这个平面。

• 既然垂直于平面，那么 $e$ 必须垂直于平面上的所有基向量（即 $X$ 的每一列）。
• 用数学语言描述“垂直”就是内积为 0。

所以，$X$ 的每一列与 $e$ 的点积都为 0：

$$X^T\cdot e=0$$

代入 $e=Y-X\theta$：

$$X^T(Y-X\theta )=0$$

展开：

$$X^{T}Y-X^{T}X\theta =0$$

$$X^{T}X\theta =X^{T}Y$$

图片放的不合适，但是可以作为一个参考吧，具体的看原文。

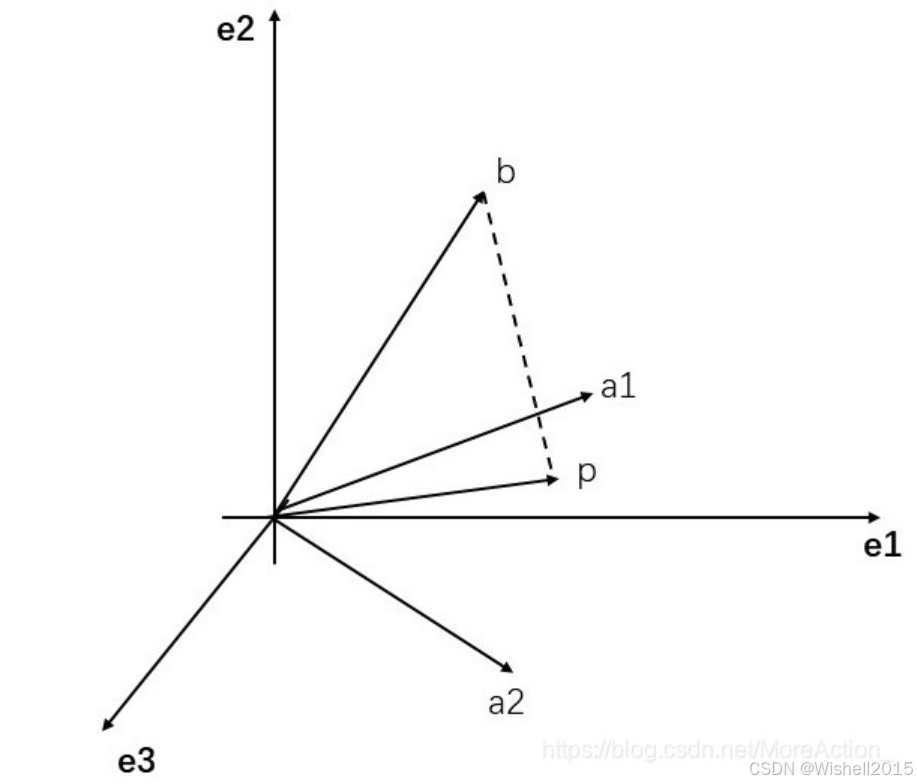
可以参考https://blog.youkuaiyun.com/MoreAction_/article/details/106443383?ops_request_misc=%257B%2522request%255Fid%2522%253A%25227ef8c0683c2dd970ff9fb57930568291%2522%252C%2522scm%2522%253A%252220140713.130102334…%2522%257D&request_id=7ef8c0683c2dd970ff9fb57930568291&biz_id=0&spm=1018.2226.3001.4187这篇文章。

‍

以二维举例：

假设我们在一个 3维空间里。有两个基准向量 $x_1$ 和 $x_2$。它们定义了一个平面。要寻找这两个向量的组合，去够那个飘在空中的点 $Y$。

具体的数值例子：

• $x_1$ (红色箭头) ：躺在 x 轴上 $\to [1,0,0{]}^T$
• $x_2$ (蓝色箭头) ：躺在 y 轴上 $\to [0,1,0{]}^T$
• $Y$ (空中的星星) ：悬浮在半空 $\to [1,2,3{]}^T$

显然，$x_1$ 和 $x_2$ 无论怎么组合（${\theta }_1{x}_1+{\theta }_2{x}_2$），结果的第三个分量永远是 0。这意味着：永远无法用 $x_1$ 和 $x_2$ 完美组合出 $Y$（因为 $Y$ 的高度是 3）。

目标是找到一组系数 ${\theta }_1,{\theta }_2$，使得组合出来的向量 $\hat{Y}$（预测值）离 $Y$ 最近。

直觉：$Y$ 在地板上的垂直投影就是最近的点。

预测向量：$\hat{Y}={\theta }_1{x}_1+{\theta }_2{x}_2$。

误差向量：$e=Y-\hat{Y}$。为了让距离最短，误差线 $e$ 必须垂直于地板。

为什么是“点积为 0”？ 如果误差线 $e$ 垂直于整个地板，那么它必须垂直于地板上的每一根经纬线。
也就是：

1. $e$ 必须垂直于 $x_1$。
2. $e$ 必须垂直于 $x_2$。

数学翻译（垂直 = 点积为 0） ：

$$\{\begin{array}{l}{x}_1^T\cdot e=0\\ x_2^T\cdot e=0\end{array}$$

把具体的数字代进去看看：预测值显然应该是影子的坐标 $\hat{Y}=[1,2,0{]}^T$。
那么误差向量就是 $e=[1,2,3]-[1,2,0]=[0,0,3{]}^T$（一根竖直向上的线）。

验证垂直性：

1. $x_1\cdot e=[1,0,0]\cdot [0,0,3]=0$ （没毛病，垂直）
2. $x_2\cdot e=[0,1,0]\cdot [0,0,3]=0$ （没毛病，垂直）

矩阵化：​$X^T$ 的诞生

把 $x_1^T$ 和 $x_2^T$ 叠在一起，这不就是矩阵 $X^T$ 吗？

$$\underset{X^T}{\underbrace{\left[\begin{array}{c}{x}_1^T\\ x_2^T\end{array}\right]}}\cdot e=\left[\begin{array}{c}0\\ 0\end{array}\right]$$

所以几何条件变成了：$X^{T}e=0$。

重点：这里的 $X^T$ 作用就是—— “一次性检查误差向量 $e$ 是否垂直于所有的基向量” 。

求解 $\theta$：

将 $e=Y-X\theta$ 代入：

$$X^T(Y-X\theta )=0$$

展开：

1. $X^{T}Y-X^{T}X\theta =0$
2. $X^{T}X\theta =X^{T}Y$

代入数值计算验证一下：

1. 构造 $X$：

   $$X=\left[\begin{array}{cc}1& 0\\ 0& 1\\ 0& 0\end{array}\right]$$

2. 计算 $X^{T}Y$ (投影分量) ：

   $$X^{T}Y=\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\end{array}\right]\left[\begin{array}{c}1\\ 2\\ 3\end{array}\right]=\left[\begin{array}{c}1\\ 2\end{array}\right]$$

3. 计算 $X^{T}X$ (坐标系校正) ：

   $$X^{T}X=\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\end{array}\right]\left[\begin{array}{cc}1& 0\\ 0& 1\\ 0& 0\end{array}\right]=\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]$$

4. 解方程：

   $$\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]\theta =\left[\begin{array}{c}1\\ 2\end{array}\right]$$

   显然：

   $$\theta =\left[\begin{array}{c}1\\ 2\end{array}\right]$$

结论：
我们算出 ${\theta }_1=1,{\theta }_2=2$。
预测值 $\hat{Y}=1\cdot x_1+2\cdot x_2=[1,2,0{]}^T$。

‍

与最大似然估计的联系

简单来说：最小二乘法是最大似然估计在“误差服从正态分布”这个特定假设下的一种特殊情况。

一、 什么是最大似然估计 (MLE)？

Maximum Likelihood Estimation (MLE) 是一种统计方法，用来估计模型的参数。

1. 直观理解：侦探视角

假设你是一个侦探，来到了案发现场（这就是你拿到的数据）。你需要推断凶手是谁、作案手法是什么（这就是模型参数）。

• 概率（Probability） ：已知参数，预测数据。

  • 例子：已知硬币是均匀的（参数），扔10次，出现5正5反的概率是多少？

• 似然（Likelihood） ：已知数据，推断参数。

  • 例子：不知道硬币均不均匀，但我扔了10次，全是正面（数据）。请问，这枚硬币“动过手脚”的可能性有多大？
  • MLE的逻辑：既然我抛出了10次全是正面，那么“这枚硬币两面都是正面”这个参数假设，虽然不一定对，但最能解释当前的数据。

MLE的核心思想：
找到一组参数 $\theta$，使得在这组参数下，出现当前数据的概率最大。

---

二、 最小二乘法与 MLE 的联系（数学推导）

为什么说最小二乘法是 MLE 的一种特例？我们通过线性回归来推导。

1. 设定假设

在线性回归中，假设真实值 $y$ 和预测值 $Xw$ 之间有一个误差 $ϵ$：

$$y=Xw+ϵ$$

关键步骤来了！ 必须对这个误差 $ϵ$ 做一个假设。通常假设误差服从高斯分布（正态分布） ，且均值为0，方差为 ${\sigma }^2$。

$$ϵ\sim N(0,{\sigma }^2)$$

这意味着，给定 $x$ 和 $w$，真实标签 $y$ 也服从正态分布，其均值是 $Xw$：

$$y\sim N(Xw,{\sigma }^2)$$

2. 写出概率密度函数

根据正态分布公式，某一个样本点 $y_i$ 出现的概率密度是：

$$P(y_i|x_i;w)=\frac{1}{\sqrt{2\pi }\sigma }\exp \left(-\frac{(y_i-w^T{x}_i{)}^2}{2{\sigma }^2}\right)$$

3. 写出似然函数 (Likelihood Function)

因为样本之间是独立的，所以所有样本同时出现的概率（似然函数 $L(w)$）就是把每一个样本的概率乘起来：

$$L(w)=\prod _{i=1}^{n}P(y_i|x_i;w)=\prod _{i=1}^n\frac{1}{\sqrt{2\pi }\sigma }\exp \left(-\frac{(y_i-w^T{x}_i{)}^2}{2{\sigma }^2}\right)$$

4. 最大化似然函数

要找到 $w$ 让 $L(w)$ 最大。连乘很难算，为了方便计算，取对数（Log-Likelihood）。因为对数函数是单调增的，最大化对数似然等价于最大化原函数。

$$\ln L(w)=\sum _{i=1}^n\ln \left[\frac{1}{\sqrt{2\pi }\sigma }\exp \left(-\frac{(y_i-w^T{x}_i{)}^2}{2{\sigma }^2}\right)\right]$$

利用对数性质 $\ln (ab)=\ln a+\ln b$，展开：

$$\ln L(w)=\sum _{i=1}^n\left[\ln (\frac{1}{\sqrt{2\pi }\sigma })-\frac{(y_i-w^T{x}_i{)}^2}{2{\sigma }^2}\right]$$

5. 见证奇迹的时刻

要最大化这个 $\ln L(w)$。

• 第一项 $\sum \ln (\frac{1}{\sqrt{2\pi }\sigma })$ 是常数（和 $w$ 无关），求导时直接为0，可以忽略。

• 剩下的就是要最大化：

  $$

  • \sum_{i=1}^n \frac{(y_i - w^T x_i)^2}{2\sigma2}
    $$

最大化一个负数，等价于最小化那个正数（去掉负号） 。
同时，$\frac{1}{2{\sigma }^2}$ 也是常数系数，不影响求极值的位置。

所以，最大化似然函数，最终等价于：

$$\text{最小化}\sum _{i=1}^n(y_i-w^T{x}_i{)}^2$$

看！这不就是最小二乘法的公式吗？

1. 这种联系说明了什么？

• 最小二乘法（Least Squares） 是从几何角度（距离最小）或代数角度出发的。
• 最大似然估计（MLE） 是从概率统计角度出发的。
• 联系：如果你假设数据中的噪声是正态分布的，那么这两种方法求出来的解是完全一样的。

2. 如果噪声不是正态分布呢？

这就体现出 MLE 的普适性了。

• 如果误差服从拉普拉斯分布（Laplace Distribution，尖峰更厚），推导出的 MLE 等价于 最小化绝对值误差（L1 Loss） ，也就是 Lasso 回归的基础。
• 如果误差服从泊松分布（Poisson Distribution），推导出的就是广义线性模型中的泊松回归。

最小二乘法之所以好用，是因为在自然界中，大多数误差确实服从正态分布（中心极限定理）。它是最大似然估计在高斯噪声假设下的完美替身。

‍

Tips：

• 残差=真实值-预测值
• 物理、数学在某些意义上的统一，确实牛皮