647. 回文子串

思路
- dp[i][j]:表示区间范围[i,j] (注意是左闭右闭)的子串是否是回文子串,如果是dp[i][j]为true,否则为false。
- 递推公式
- s[i]与s[j]不相等
- 那没啥好说的了,dp[i][j]一定是false。
- s[i]与s[j]相等时
- 情况一:下标i 与 j相同,同一个字符例如a,当然是回文子串
- 情况二:下标i 与 j相差为1,例如aa,也是回文子串
- 情况三:下标:i 与 j相差大于1的时候,例如cabac,此时s[i]与s[j]已经相同了,我们看i到j区间是不是回文子串就看aba是不是回文就可以了,那么aba的区间就是 i+1 与 j-1区间,这个区间是不是回文就看dp[i + 1][j - 1]是否为true。
- s[i]与s[j]不相等
- 初始化:全部为false
- 遍历顺序,因为递推公式需要用到dp[i + 1][j - 1],在dp[i][j]的左下角。所以遍历顺序需要从下往上,从左到右

- 举例推导dp: 输入:“aaa”,dp[i][j]状态如下:

思路2 双指针
通过遍历每个回文中心,向两边扩散,并判断是否回文字串。在遍历中心点的时候,要注意中心点有两种情况。一个元素可以作为中心点,两个元素也可以作为中心点。
代码
dp
class Solution:
def countSubstrings(self, s: str) -> int:
dp = [[False] * len(s) for _ in range(len(s))]
res = 0
for i in range(len(s) - 1, -1, -1):
for j in range(i, len(s)):
if s[i] == s[j]:
if j - i <= 1: # 情况1 和 情况2
dp[i][j] = True
res += 1
elif dp[i + 1][j - 1]: # 情况3
dp[i][j] = True
res += 1
return res
- 时间复杂度:
O(n^2) - 空间复杂度:
O(n^2)
双指针
class Solution:
def countSubstrings(self, s: str) -> int:
res = 0
for i in range(len(s)):
l, r = i, i
# odd case
while l >= 0 and r < len(s) and s[l] == s[r]:
res += 1
l -= 1
r += 1
# even case
l, r = i, i+1
while l >= 0 and r < len(s) and s[r] == s[l]:
res += 1
l -= 1
r += 1
return res
- 时间复杂度:
O(n^2) - 空间复杂度:
O(1)
516.最长回文子序列

思路
-
dp[i][j]:字符串s在[i, j]范围内最长的回文子序列的长度为dp[i][j]。
-
递推公式:
- s[i]与s[j]相同,那么
dp[i][j] = dp[i + 1][j - 1] + 2

- s[i]与s[j]不相同,说明s[i]和s[j]的同时加入 并不能增加[i,j]区间回文子序列的长度,那么分别加入s[i]、s[j]看看哪一个可以组成最长的回文子序列。
- 加入s[j]的回文子序列长度为dp[i + 1][j]
- 加入s[i]的回文子序列长度为dp[i][j - 1]
- 那么dp[i][j]一定是取最大的,即:
dp[i][j] = max(dp[i + 1][j], dp[i][j - 1])

- s[i]与s[j]相同,那么
-
初始化:其他为0,dp[i][i] = 1
-
遍历顺序:从下到上,从左到右
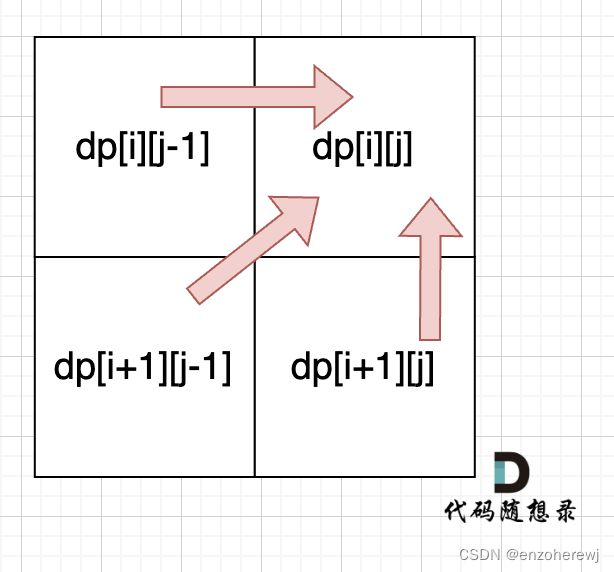
-
举例推导:输入s:“cbbd” 为例,dp数组状态如图:

代码
class Solution:
def longestPalindromeSubseq(self, s: str) -> int:
dp = [[0] * len(s) for _ in range(len(s))]
for i in range(len(s)):
dp[i][i] = 1
for i in range(len(s) - 1, -1, -1):
for j in range(i + 1, len(s)):
if s[i] == s[j]:
dp[i][j] = dp[i + 1][j - 1] + 2
else:
dp[i][j] = max(dp[i + 1][j], dp[i][j - 1])
return dp[0][-1]
- 时间复杂度:
O(n^2) - 空间复杂度:
O(n^2)





 博客围绕LeetCode的647.回文子串和516.最长回文子序列问题展开。对于回文子串,介绍了动态规划和双指针两种解法;对于最长回文子序列,采用动态规划求解。详细阐述了状态定义、递推公式、初始化和遍历顺序等内容。
博客围绕LeetCode的647.回文子串和516.最长回文子序列问题展开。对于回文子串,介绍了动态规划和双指针两种解法;对于最长回文子序列,采用动态规划求解。详细阐述了状态定义、递推公式、初始化和遍历顺序等内容。
















 512
512

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








