6.6.1 赫夫曼树

赫夫曼树

• 又叫做最优树；可以是最优二叉树，也可以是最优多分支树。
  本次只讨论最优二叉树。
  赫夫曼树中没有度为1的结点。

最优二叉树

• 常用定义
  路径：从树中一个结点到另一个结点之间的分支就构成了这两个结点之间的路径。
  路径长度：路径上的分支数目 (有几根线)。
  树的路径长度：从树根到每一结点的路径长度之和。
  结点的权：由实际问题来决定。一般就是结点数据域的值。（如报文问题中，每种报文字符出现的次数）
  结点的带权路径长度：从该结点到树根之间的路径长度与该结点的权的乘积。
  树的带权路径长度：树中所有叶子结点的带权路径长度之和。WPL = ∑ W_k * L_k
  最优二叉树 / 赫夫曼树：假设有n个权值{ W₁ , W₂ , … , W_n } , 试构造一棵有n个叶子结点的二叉树，每个叶子结点带权为W_i , 则其中带权路径长度 WPL 最小的二叉树称为最优二叉树 / 赫夫曼树。

• 示例
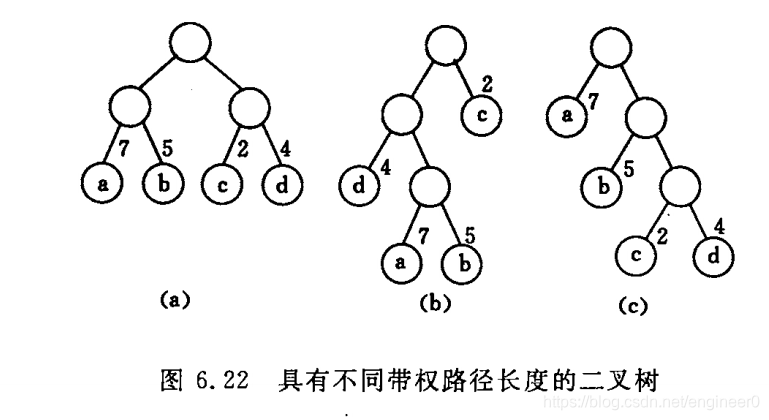
  如下图，3棵二叉树，每个都有4个叶子结点a , b , c , d，分别带权 7 , 5 , 2 , 4。
  (a) WPL = 7 * 2 + 5 * 2 + 2 * 2 + 4 * 2 = 36
  (b) WPL = 4 * 2 + 7 * 3 + 5 * 3 + 2 * 1 = 46
  © WPL = 7 * 1 + 5 * 2 + 3 * 2 + 4 * 3 = 35
  树c 的 叶子结点带权路径长度和最小，所以树c 是赫夫曼树
  

赫夫曼算法

• 步骤
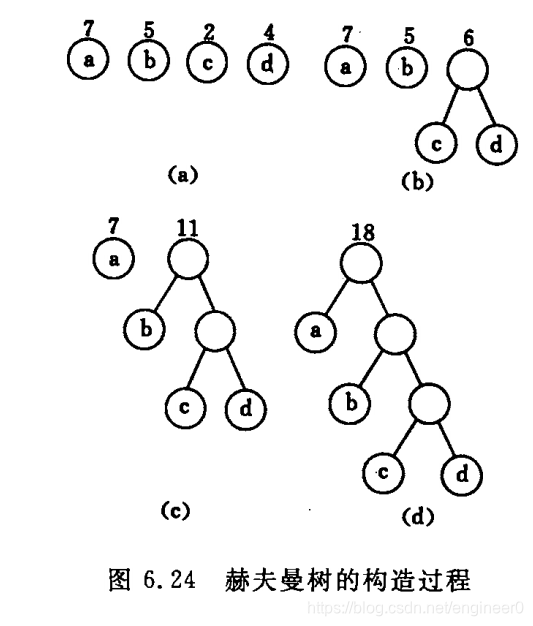
  (1) 根据给定的n个权值 { W₁ , W₂ , … , W_n } 构成n 棵二叉树的集合 F = { T₁ , T₂ , … , T_n } , 每棵二叉树 T_i 只有一个带权为 W_i 的根结点，左右子树均为空。
  (2) 在 F 中选取两棵根结点的权值最小的树作为左右子树构造一棵新的二叉树，并且置新的二叉树的根结点的权值为其左右子树上的根结点的权值之和。
  (3) 在 F 中删除这两棵树，同时将新得到的二叉树加入到 F 中。
  (4) 重复 (2) 和 (3) , 直到 F 只含一棵树为止。