6.7 回溯法和树的遍历

• 回溯法
  实质就是先序遍历一棵 “状态树” 的过程，这颗树不是遍历前预先建立的，而是在遍历过程中建立
  详细介绍：[回溯算法] 五大常用算法之回溯法

典型应用：求含n个元素的集合的幂集

集合A的幂集是由集合A的所有子集所组成的集合。如：A={ 1, 2, 3 }，则 A 的幂集 p(A) = { {1, 2, 3} , {1, 2} , {1, 3} , {2, 3} , {1} , {2} , {3} , { } }

• 幂集 p(A) 的每个元素是一个集合，它或是空集，或含集合A中的一个元素，或含集合A中的两个元素，或者等于集合A。
  从集合A来看，它的每个元素只有两种状态：或属于幂集中的某个元素集，或不属于幂集中的元素集。

• 求幂集p(A)的元素的过程可看成是依次对集合A中元素进行“取” 或者“弃”的过程。

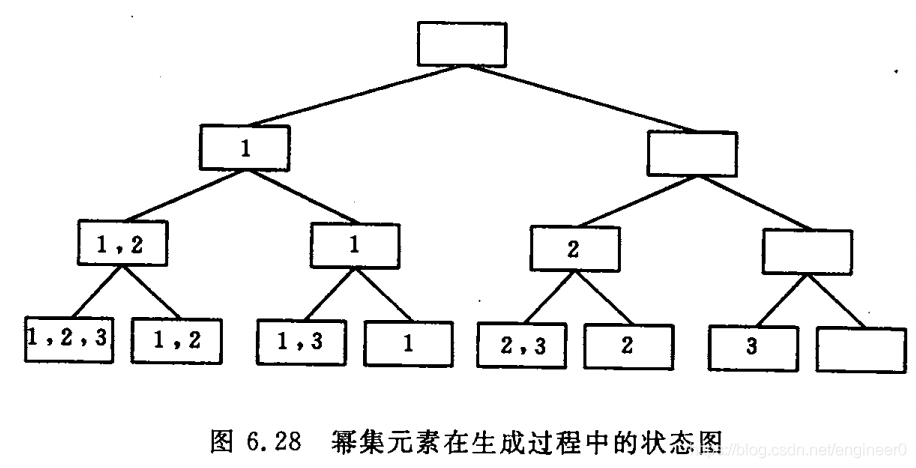
• 如下图二叉树，
  树的根结点表示幂集某个元素的初始状态（为空集）
  叶子结点表示幂集元素的终结状态（8个叶子结点表示幂集p(A)的8个元素）
  分支结点表示对集合A中前 i - 1 个元素进行取舍处理的当前状态（左分支表示取，右分支表示弃）
  综上，求幂集就是先序遍历这棵状态树的过程。
  

• 算法如下（伪码）

void PowerSet(int i, int n)
{
	// 求含n个元素的集合A的幂集p(A)。进入函数时已对A中前i-1个元素作了取舍处理
	// 现从第i个元素进行取弃处理。
	// 如i>n，则求得了p(A)的一个元素，并输出之
	// 初始调用: PowerSet(1, n)
	if(i > n) // n表示集合A的元素个数
	{
		输出幂集的一个元素;
	}
	else
	{
		取 / 弃 第i个元素;
		PowerSet(i+1, n);
	}
}

• 对上面的伪码进一步细写

void GetPowerSet(int i, List A, List &B)
{
	// 线性表A表示集合A，线性表B表示幂集p(A)的一个元素
	// 进入函数时已经对前面i-1个元素做了取舍处理
	// 第一次调用本函数时，B为空表，i=1
	if(i > ListLength(A))
	{
		// 输出当前B的值，即p(A)的一个元素
		Output(B);
	}
	else
	{
		// 获取 A 的第 i 个元素
		GetElem(A, i, x);
		// B 的当前长度
		k = ListLength(B);
		// 取 / 舍
		ListInsert(B, k+1, x); / ListDelete(B, k+1, x);
		GetPowerSet(i+1, A, B);
	}
}