6.4.1 树的存储结构

前言

• 实际情况中，多分支树比二叉树更为常见和实用。
• 树的存储结构有很多种形式，本文介绍常用的三种
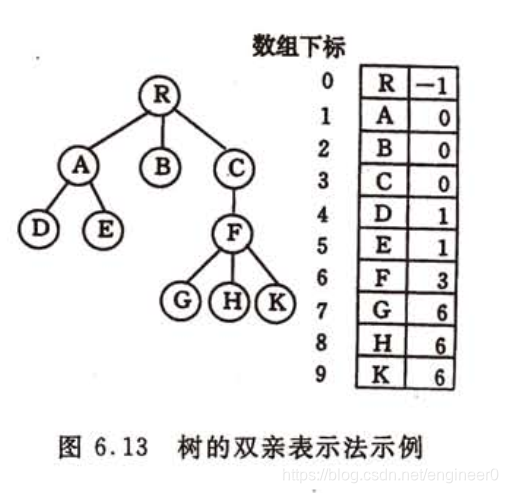
  1、双亲表示法
  2、孩子表示法
  3、孩子兄弟表示法

1、双亲表示法

• 以一组连续空间来存储树的结点。
• 每个结点附设一个指示器来指示其双亲结点在表中的位置。
• 只有根结点没有双亲结点，其它结点有且只有一个双亲结点。
• 不足：确定某个结点的孩子结点时需要遍历整个结构。

#define MAX_TREE_SIZE 100
// 以下结构描述单个结点结构
typedef struct PTNode
{
	TElemType data; // 结点数据域
	int parent; // 双亲位置域，指示双亲的在表中的下标
} PTNode;
// 以下结构描述树结构
typedef struct
{
	PTNode nodes[MAX_TREE_SIZE];// 顺序表存放所有结点
	int r, n; // r 为根的下标，n 为结点总数
} PTree;

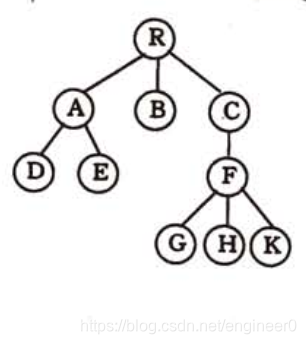
2、孩子表示法

• 一般来说，树中的每个结点可能有多个子树，每个结点需要有多个指针域。

---

引出两种结点格式：

• 1、多重链表中的每一个结点都是同构的，每个结点结构都有 d 个指针域，d 称为树的度。
  缺点是树中的许多结点的度可能小于d，造成很多空链域，浪费空间。
  而且，在一棵度为d，有 n 个结点的树中，必有 n * ( d - 1 ) + 1个空链域。
  结点结构如下图。
  

• 2、多重链表中的各个结点不同构。
  即每个结点的度是可变的，一般增设一个域 degree 来指示某个结点的度是多少。
  如下图
  

---

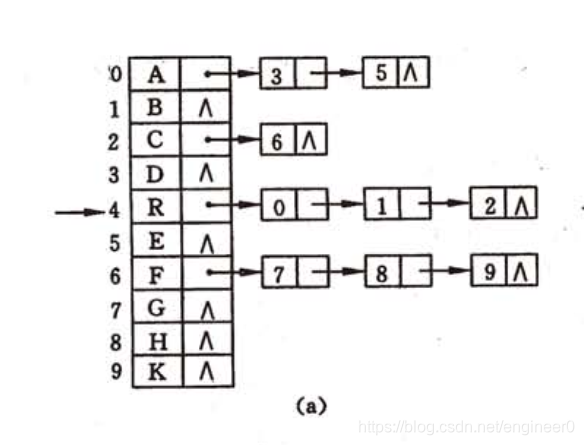
• 推荐的方法是
  把每个结点的所有孩子结点排列成一个单链表（线性表），
  把每个结点视为根结点，所有根结点组成一个顺序表。
  那么 n 个结点则有 n 个孩子链表。n 个头指针又组成一个顺序表 (线性表)。

// 孩子链表的中的一个结点结构
typedef struct CTNode
{
	// 不需要在此类型结构中设置数据域
	int child; // 顺序表中的标号
	struct CTNode *next; 
} *ChildPtr;

// 根结点（由此类型组成顺序表）
typedef struct
{
	TElemType data; // 结点数据域，孩子链表结点中不需要有数据域
	ChildPtr firstChild; // 根结点的孩子结点链表
} CTBox;

// 整棵树
typedef struct
{
	CTBox nodes[MAX_TREE_SIZE]; // 树中所有结点构成一个顺序表
	int n , r; // n 为结点的下标，r 为结点总数
}

• 如下图示，
  
  

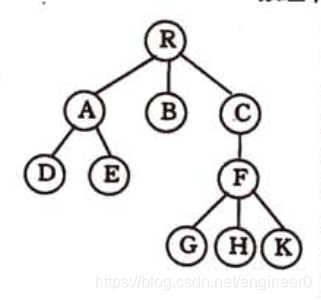
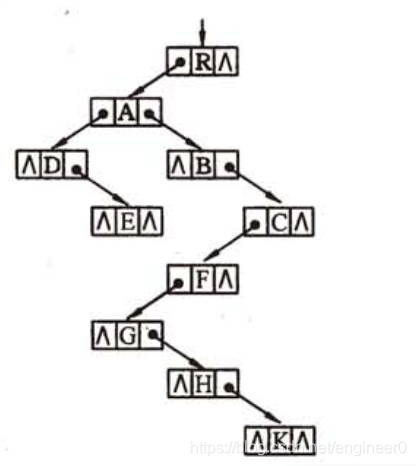
3、孩子兄弟表示法 ( common!!! )

• 又叫二叉树表示法，二叉链表表示法。
• 以二叉链表作为树的存储结构。
• 每个结点都有两个链域，分别指向该结点的第一个孩子结点，该结点的下一个兄弟结点。
  存储结构如下

typedef struct CSNode
{
	ElemType data;
	struct CSNode *firstChild, *nextSibling;
} CSNode, *CSTree;

• 二叉链表表示二叉树时，结点的左右两链域都是其孩子结点。

• 二叉链表表示树时，结点的左链域是孩子，右链域是其下一个兄弟结点。
  一个结点和它的左子树便可表示以该结点为根结点的子树。
  若要访问某结点的第i个孩子，则只要先从firstChild域找到第1个孩子结点，然后沿着这个孩子结点的nextSibling域连续走i - 1步，便可找到第i个孩子。

• 如下图