7.2.1 二维数组 / 邻接矩阵表示法

图和它的邻接矩阵示例

• G₁ 是有向图，G₂ 是无向图，无向图的邻接矩阵是对称的。
  

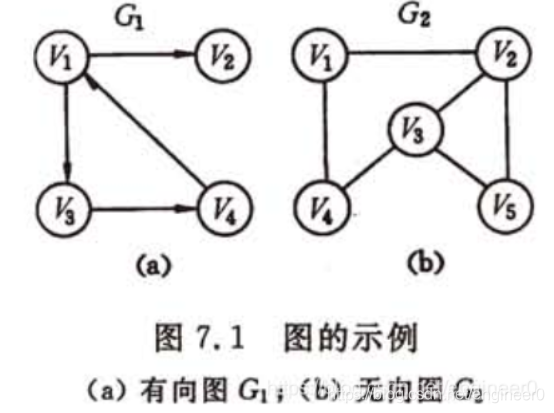
• 可以借助邻接矩阵判断两个顶点之间是否有弧或者边相连。
  有向图中包括顶点和弧
无向图中包括顶点和边
  对于无向图：顶点 v_i 的度是第 i 行的元素和 或者 第 i 列的元素和
  对于有向图：顶点 v_i 的出度是第 i 行的元素和，入度是第 j 列的元素和

有向网和它的邻接矩阵示例

• 定义
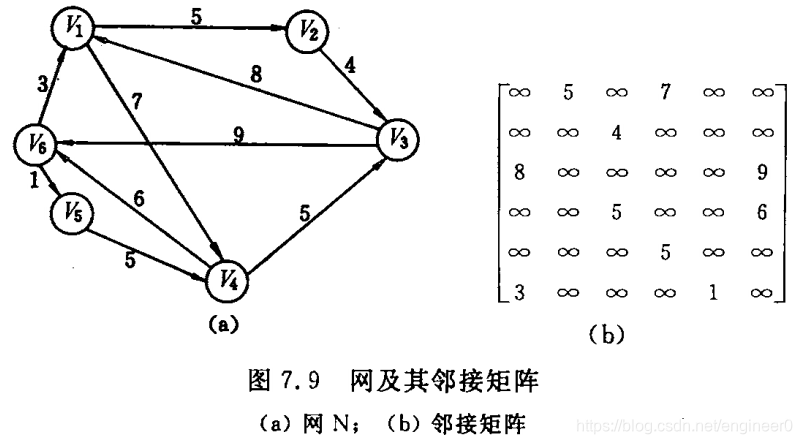
  下图 w_i，j 为 顶点 v_i 和 v_j 构成的弧的权值。
  
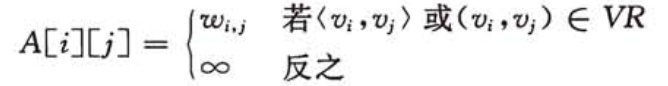
• 示例
  

数组表示法相关 存储结构

• 用两个数组分别存储数据元素（顶点）的信息 和 数据元素之间的关系（边或弧）的信息。

#define INFINITY        INT_MAX     // 最大值 / 无穷大
#define MAX_VERTEX_NUM  20			// 最大顶点个数

// 此数据类型表示图的类型
typedef enum
{
	DG,		// 有向图
	DN,		// 有向网
	UDG,	// 无向图
	UDN		// 无向网
} GraphKind;

typedef struct ArcCell
{
	VRType adj;		//顶点关系类型，
					//无权图用1和0表示相邻和不相邻
					//带权图则表示权值类型
	InfoType *info; //该弧相关信息的指针
} ArcCell, AdjMatrix[MAX_VERTEX_NUM][MAX_VERTEX_NUM];
// 上面这个二维数组类型表示

// 有n个顶点的图需要存放 n 个顶点信息和 n*n 个弧信息
typedef struct
{
	VertexType vexs[MAX_VERTEX_NUM];	//顶点向量 / 顶点信息
	AdjMatrix arcs;						//邻接矩阵 / 弧信息
	int vexnum, arcnum;					//图的顶点数和弧数
	GraphKind kind;						//图的种类标志
} MGraph;

构造图G算法（基于结构 MGraph）

// 有 n 个顶点的图需要存放 n 个顶点信息和 n*n 个弧信息
typedef struct
{
	VertexType vexs[MAX_VERTEX_NUM];	//顶点向量 / 顶点信息
	AdjMatrix arcs;						//邻接矩阵 / 弧信息
	int vexnum, arcnum;					//图的顶点数和弧数
	GraphKind kind;						//图的种类标志
} MGraph;

Status CreateGraph(MGraph &G)
{
	// 采用数组（邻接矩阵）表示法，构造图 G
	scanf(&G.kind);
	switch(G.kind)
	{
		case DG: return CreateDG(G);	//构造有向图
		case DN: return CreateDN(G);	//构造有向网
		case UDG： return CreateUDG(G); //构造无向图
		case UDN： return CreateUDN(G); //构造无向网
		default: return ERROR;
	}
}
// 以构造 无向网 为例
Status CreateUDN(MGraph &G)
{
	// 采用数组（邻接矩阵）表示法，构造无向网
	scanf(&G.vexnum, &G.arcnum, &IncInfo);
	for(i=0; i<G.vexnum; ++i)
	{
		scanf(&G.vexs[i]); //构造顶点向量
	}
	for(i=0; i<G.vexnum; ++i) // 初始化邻接矩阵
	{
		for(j=0; j<G.vexnum; ++j)
		{
			G.arcs[i][j] = {INFINITY, NULL};
		}
	}
	for(k=0; k<G.arcnum; ++k) // 构造邻接矩阵
	{
		scanf(&v1, &v2, &w); // 输入一条边依附的顶点及权值
		i = LocateVex(G, v1); //确定 v1,v2 在图中的位置
		j = LocateVex(G, v2); //即v1,v2在一维数组vexs中的位置 / 下标
		G.arcs[i][j].adj = w; //<v1, v2> 的权值
		G.arcs[j][i].adj = G.arcs[i][j].adj；
		if(IncInfo)
		{
			// 若弧含有相关信息，则输入
			Input(*G.arcs[i][j].info);
		}
	}
	return OK;
}

• 时间复杂度
  利用上述算法构造一个具有 n 个顶点和 e 条边的无向网 G 的时间复杂度是 O( n² + e * n )，
  对邻接矩阵的初始化耗费了 O( n² ) 。