二分图

二分图

一、二分图定义
大概就是在一个图G(S,V)中，可以把点集S分成两个集合使同一个集合中的点之间没有边相连；
比如说这个：

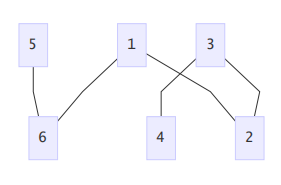
这个很简单，不知道的可以自行查阅有关资料；
二、二分图的匹配
什么叫二分图的匹配呢？
把二分图的两个点集中有边相连的边”匹配在一起“就叫二分图的匹配；
比如说上图中我把1与2配对，3与4配对，5与6配对，这就是二分图的一组匹配；
而看到这里我们可以自然而然的引出一个问题——怎么可以让一个二分图在匹配之后配对的对数最多？
这就是二分图的最大匹配问题；
我们来看这样一个例子：
有n个男的，m个女的，每个男的有一些喜欢的女的（而且这个喜欢都是相互的），当然每个男的都只能和一个女的
修成正果~不要问我为什么，问你最多会有几对情侣？
这就是二分图最大匹配的最典型例子（当媒婆）。那么我们要怎么才能解决这个问题呢？
这时候我们就要用一种叫匈牙利算法的算法（当然可以用网络流），在学习这种算法之前我们要了解一个新的概念
——二分图的增广路；
什么叫增广路呢？
增广路径是指，由一个未匹配的顶点开始，经过若干个匹配顶点，最后到达对面集合的一个未匹配顶点的路径，即这
条路径将两个不同集合的两个未匹配顶点通过一系列匹配顶点相连；
我们把增广路上的每条边的状态取反（已匹配变成未匹配，未匹配变成已匹配）就会发现端点的两个未匹配点都变成
了匹配点，其他的点状态不变，于是就多了一对匹配；
匈牙利算法就是通过不断寻找增广路来实现最大匹配的；
模板如下：

#include<bits/stdc++.h>
using namespace std;
struct node
{
int v,next;
node(int a,int b)
{
v=a;
next=b;
}
node(){}
}ma[1000010];
int t=0,head[2010],n,m,e,k=0;
bool vis[2010],pi[2010],mem[2010];
void add(int a,int b)
{
ma[++k]=node(b,head[a]);
head[a]=k;
}
bool flag;
bool Hun(int x)
{
if(mem[x]==1) return 0;
vis[x]=1;
for(int i=head[x];~i;i=ma[i].next)
{
if(vis[ma[i].v]) continue;
else if(ma[i].v<=n&&!pi[ma[i].v]) continue;
else if(ma[i].v>n&&!pi[ma[i].v])
{
pi[ma[i].v]=1;
return 1;
}
else if(Hun(ma[i].v)) return 1;
}
mem[x]=1;
return 0;
}
int main()
{//freopen("testdata.in","r",stdin);
memset(head,-1,sizeof(head));
int ans=0;
cin>>n>>m>>e;
for(int i=1;i<=e;i++)
{//cout<<i<<endl;
int a,b;
cin>>a>>b;
if(a>n||b>m) continue;
b+=n;
add(a,b);
add(b,a);
}
for(int i=1;i<=n;i++)
{
memset(vis,0,sizeof(vis));
if(Hun(i)) ans++,pi[i]=1;
}
cout<<ans;
}

我们就这么完美的解决了这个问题 不算长
那么问题又来了——如果一个男的可以和多个女的修成正果（反之亦然）的话，这垃圾算法不就废了吗？
No,no,no！你们太天真了，这其实可以用巧妙的一个方法破解掉——拆点；
比如一个男的可以**k个女的，你就只需要把他当成k个人就行了~~（他精神分裂，每一重人格嗯哼一个女的，嗯~）
那么问题又来了，如果边有权值的话怎么办？
哼哼，你们以为我大匈牙利算法就这样就会痿了？没错它就是痿了！
那我们应该怎么办呢？
这时候就要用到一个叫KM算法的垃圾算法了；
But，我们今天不讲了，哈哈，气不气；