SLAM十四讲 5.4 实践：拼接点云 | Python Numpy实现 & 坑

问题理解

给定了每张图像和估计好的深度图，也给定了相机外参和内参（内参cx, cy = 325.5,253.5，fx, fy = 518.0, 519.0），首先按照相机内参将像素按照深度值投影到相机3D坐标系下，再统一所有相机的视点到世界坐标系下组成一份完整的点云

输入数据

第一步

将每张图像的(u, v)坐标转换到相机的3D坐标系下，即$P_{uv}\to P_c$，我们先来看相机模型的坐标转换公式

$$Z\left(\begin{array}{c}u\\ v\\ 1\end{array}\right)=\left(\begin{array}{c}{f}_{x}0c_x\\ 0f_y{c}_y\\ 001\end{array}\right)\left(\begin{array}{c}{X}_c\\ Y_c\\ Z_c\end{array}\right)$$

现在是已经$Z$也就是深度值，那就依次遍历每个像素位置，将每个像素转换为相机坐标系下的3D点

$$\{\begin{array}{llc}{X}_c& =& \frac{u-c_x}{f_x}Z\\ Y_c& =& \frac{v-c_y}{f_y}Z\\ Z_c& =& Z\end{array}$$

得到了相机坐标系下的3D点其实就是点云了，直接将各个深度图对应的点云保存也可以，但可以发现各个点云的坐标系不同，他们对不上

相机坐标系下的3D点，不同点云对不齐

第二步

所以下一步就是把相机坐标系转换为世界坐标系，即$P_c\to P_w$，我们再来看相机模型的坐标系转换公式

$$\left(\begin{array}{c}{X}_c\\ Y_c\\ Z_c\end{array}\right)=R\left(\begin{array}{c}{X}_w\\ Y_w\\ Z_w\end{array}\right)+t$$

或者将旋转矩阵$R$和平移向量$t$打包成$4\times 4$的变换矩阵$T$，上式可以写成

$$\left(\begin{array}{c}{X}_c\\ Y_c\\ Z_c\end{array}\right)=T\left(\begin{array}{c}{X}_w\\ Y_w\\ Z_w\end{array}\right)$$

我们现在是有了$P_c$，要求$P_w$，直接把上式左右两端乘$T^{-1}$即可，或者按照上上式那样减t再左乘$R^{-1}$

个人认为题目中说相机位姿是$T_{wc}$错了，题目中的位姿给的应该是$T_{c2w}$，所以在实现代码中可以看到直接左乘pose即可，不用将其转为逆

最终结果为：

我们这么转换相当于把所有相机坐标都变成原点对应的世界坐标，还有另一种思路是我们将第一个视点作为基准，让所有人都变换到它身上，这就回到了这道题的问题上了👇，也就是先左乘自己的变换矩阵的逆再左乘第一个视点的变换矩阵（因为题目中的相机参数给反了，所以代码里这里也是反的）

https://zhuanlan.zhihu.com/p/686975855

以世界原点为基准 vs 以第一个视点为基准，可以看到是不一样的

Python代码

import os
import numpy as np
import cv2
import open3d as o3d
from scipy.spatial.transform import Rotation
import matplotlib.pyplot as plt

images, depths = [], []
total_num = 5
for i in range(1, total_num+1):
    images.append(cv2.imread(f"color/{i}.png"))
    depths.append(cv2.imread(f"depth/{i}.pgm", cv2.IMREAD_UNCHANGED))

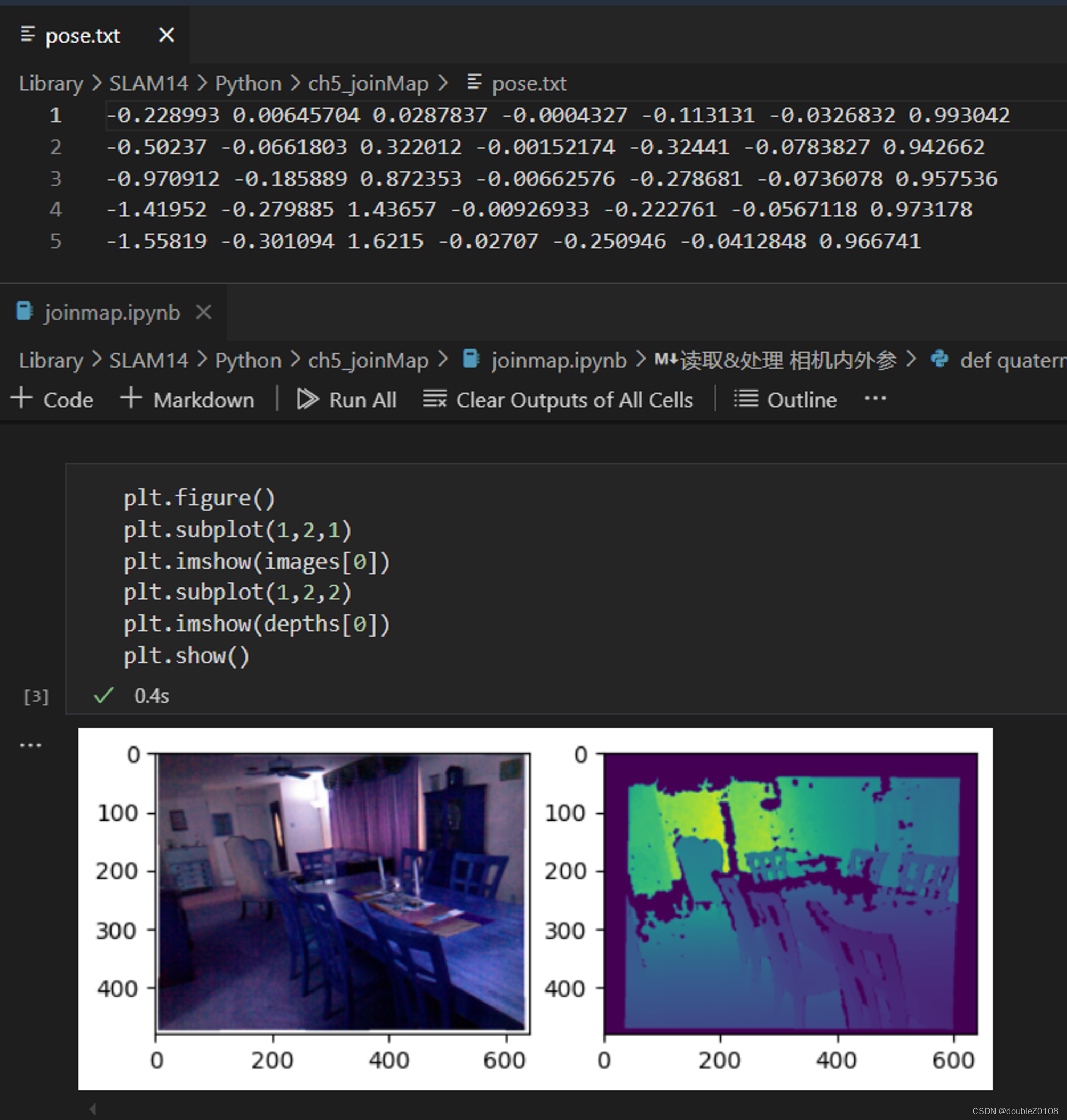
plt.figure()
plt.subplot(1,2,1)
plt.imshow(images[0])
plt.subplot(1,2,2)
plt.imshow(depths[0])
plt.show()


def quaternion2rot(quaternion):
    r = Rotation.from_quat(quaternion)
    rot = r.as_matrix()
    return rot

poses = []
with open("pose.txt", "r") as f:
    lines = f.readlines()

for line in lines:
    data = list(map(lambda x: float(x), line.split(' ')))
    t = data[0:3]
    x, y, z, w = data[3:]
    q = np.array([x, y, z, w])
    
    R = quaternion2rot(q)
    T = np.eye(4)
    T[0:3,0:3] = R
    T[0:3, -1] = t
    
    poses.append(T)

cx, cy = 325.5,253.5
fx, fy = 518.0, 519.0
K = np.array([
    [fx, 0, cx],
    [0, fy, cy],
    [0, 0, 1],
])

depth_scale = 1000.

points = []

pose_base = poses[0]
R_base, t_base = pose_base[0:3, 0:3], pose_base[0:3, -1]

for image, depth, pose in zip(images, depths, poses):
    point = []
    height, width = image.shape[0:2]

    R, t = pose[0:3, 0:3], pose[0:3, -1]

    for v in range(height):
        for u in range(width):
            z = depth[v][u] / depth_scale
            x = (u - cx) * z / fx
            y = (v - cy) * z / fy

            Pc = np.array([x, y, z]).T

            # way1 直接根据每个视点的T_c2w，统一到原点
            Pw = pose @ np.hstack((Pc, 1))
            Pw = Pw[0:3].tolist()
            Pw.extend(image[v][u])
            point.append(Pw)

        
            # # way2 根据每个视点的R t展开计算，统一到原点
            # Pw = R @ Pc + t
            # Pw = Pw.tolist()
            # Pw.extend(image[v][u])
            # point.append(Pw)

            
            # # way3 根据每个视点的T_c2w，统一到第0个视点的pose下
            # Pw2base = np.linalg.inv(pose_base) @ pose @ np.hstack((Pc, 1))
            # Pw2base = Pw2base[0:3].tolist()
            # Pw2base.extend(image[v][u])
            # point.append(Pw2base)


            # # way4 根据每个视点的R t展开计算，统一到第0个视点的pose下
            # Pw2base = np.linalg.inv(R_base) @ (( R @ Pc + t ) - t_base)
            # Pw2base = Pw2base.tolist()
            # Pw2base.extend(image[v][u])
            # point.append(Pw2base)

    point = np.array(point)
    points.append(point)


def save_pointcloud(point, filename):
    pcd = o3d.geometry.PointCloud()
    pcd.points = o3d.utility.Vector3dVector(point[:, 0:3])
    pcd.colors = o3d.utility.Vector3dVector(point[:, 3:] / 255.)
    o3d.io.write_point_cloud(filename, pcd, write_ascii=False)

for idx, point in enumerate(points):
    save_pointcloud(point, f"result_{idx}.ply")

save_pointcloud(np.array(points).reshape(-1, 6), "result_merged.ply")

🗑坑

坑1

要注意下标问题，cv2读取的图像维度为height, width = image.shape[0:2] ，但我们一般按照先横坐标再纵坐标的方式读写二维矩阵，因此访问的时候得这样

for v in range(height):
  for u in range(width):
    image[v][u]

但你得注意，X和Y的计算还是要按照公式来，本来就是X根据u, cx, fx来算，跟你数组怎么循环没关

坑2

不懂为什么Z要除以depth_scale=1000，试过如果将scale设为1，则会得到这样的结果，最终还是分层的，当然如果将scale设置为其他值也不行

如果不除以1000的scale，点云最终还是无法对齐