14.增减字符串匹配（easy）-优快云博客

本文链接：https://blog.youkuaiyun.com/doting__/article/details/148148291

1.题目链接：

942. 增减字符串匹配 - 力扣（LeetCode）942. 增减字符串匹配 - 由范围 [0,n] 内所有整数组成的 n + 1 个整数的排列序列可以表示为长度为 n 的字符串 s ，其中: * 如果 perm[i] < perm[i + 1] ，那么 s[i] == 'I' * 如果 perm[i] > perm[i + 1] ，那么 s[i] == 'D' 给定一个字符串 s ，重构排列 perm 并返回它。如果有多个有效排列perm，则返回其中任何一个。示例 1：输入：s = "IDID"输出：[0,4,1,3,2]示例 2：输入：s = "III"输出：[0,1,2,3]示例 3：输入：s = "DDI"输出：[3,2,0,1] 提示： * 1 <= s.length <= 105 * s 只包含字符 "I" 或 "D"https://leetcode.cn/problems/di-string-match/description/2.题目描述：

由范围 [0,n] 内所有整数组成的 n + 1 个整数的排列序列可以表示为长度为 n 的字符串 s ，其中:

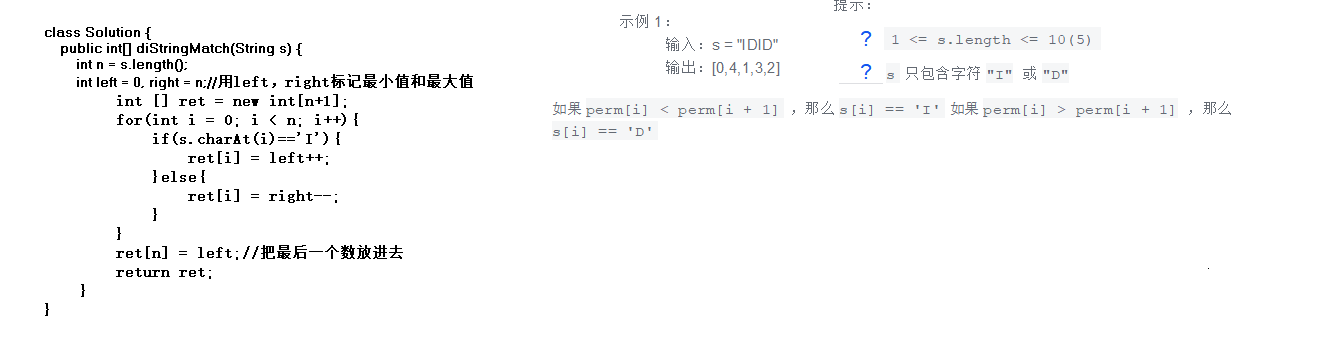
	如果 perm[i] < perm[i + 1] ，那么 s[i] == 'I' 如果 perm[i] > perm[i + 1] ，那么 s[i] == 'D'
•
•

给定一个字符串 s ，重构排列 perm 并返回它。如果有多个有效排列 perm，则返回其中任何一个。

示例 1：
        输入：s = "IDID"
        输出：[0,4,1,3,2]
示例 2：
        输入：s = "III"
        输出：[0,1,2,3]
示例 3：

输入：s = "DDI"
输出：[3,2,0,1]

提示：

◦	1 <= s.length <= 10(5)
◦	s 只包含字符 "I" 或 "D"

3. 解法（贪心）：

贪心策略：

a. 当遇到 'I' 的时候，为了让下一个上升的数可选择的「范围更多」，当前选择「最小」的那个数；

b. 当遇到 'D' 的时候，为了让下一个下降的数可选择的「范围更多」，选择当前「最大」的那个数。

Java算法代码：

class Solution {
    public int[] diStringMatch(String s) {
        int n = s.length();
        int left = 0, right = n;//用left，right标记最小值和最大值
        int [] ret = new int[n+1];
        for(int i = 0; i < n; i++){
            if(s.charAt(i)=='I'){
                ret[i] = left++;
            }else{
                ret[i] = right--;
            }
        }
        ret[n] = left;//把最后一个数放进去
        return ret;
    }
}

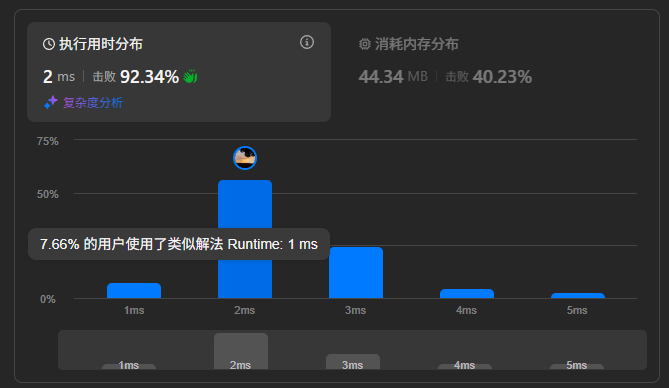
运行结果：

贪心策略：这道题目笔者觉得最重要的是读懂题目

贪心算法的体现

a. 贪心策略

局部最优：
- 当遇到 'I' 时，分配最小值 left，因为后续需要增大，留出空间给更大的值。
- 当遇到 'D' 时，分配最大值 right，因为后续需要减小，确保当前值最大。
全局最优：
- 动态调整 left 和 right，确保所有位置满足 I 或 D 的要求。
- 最后用剩余值 left 填充最后一个位置，充分利用 0 到 n 的范围。
为什么有效：
- 由于题目要求 perm 是 0 到 n 的排列，值必须用尽。
- 贪心分配最小值和最大值，保证每个位置的相对关系（< 或 >）成立。
- 最后一位必然是 left，因为 right 会在 'D' 时用完。

b. 核心位置

if (s.charAt(i) == 'I') { ret[i] = left++; }：
- 贪心选择最小值，递增 left。
else { ret[i] = right--; }：
- 贪心选择最大值，递减 right。
ret[n] = left：
- 利用剩余值填满数组，确保所有值使用。

c. 贪心正确性

数学证明：
- 假设 s 包含 k 个 'I' 和 m 个 'D'，总长度 n = k + m。
- 'I' 需要 k+1 个递增值，'D' 需要 m+1 个递减值。
- 使用 0 到 n 的值，贪心分配最小值给 'I'，最大值给 'D'，最后一位补齐。
- 由于值范围固定（0 到 n），贪心策略总能构造有效解。
与暴力方法的对比：
- 暴力方法需要尝试所有排列（O(n!)），而贪心方法只需一次遍历（O(n)）。