1.题目链接:
给定一组非负整数 nums ,重新排列每个数的顺序(每个数不可拆分)使之组成一个最大的整数。注意:输出结果可能非常大,所以你需要返回一个字符串而不是整数。
示例 1:
输入:nums = [10,2] 输出:"210"
示例 2:
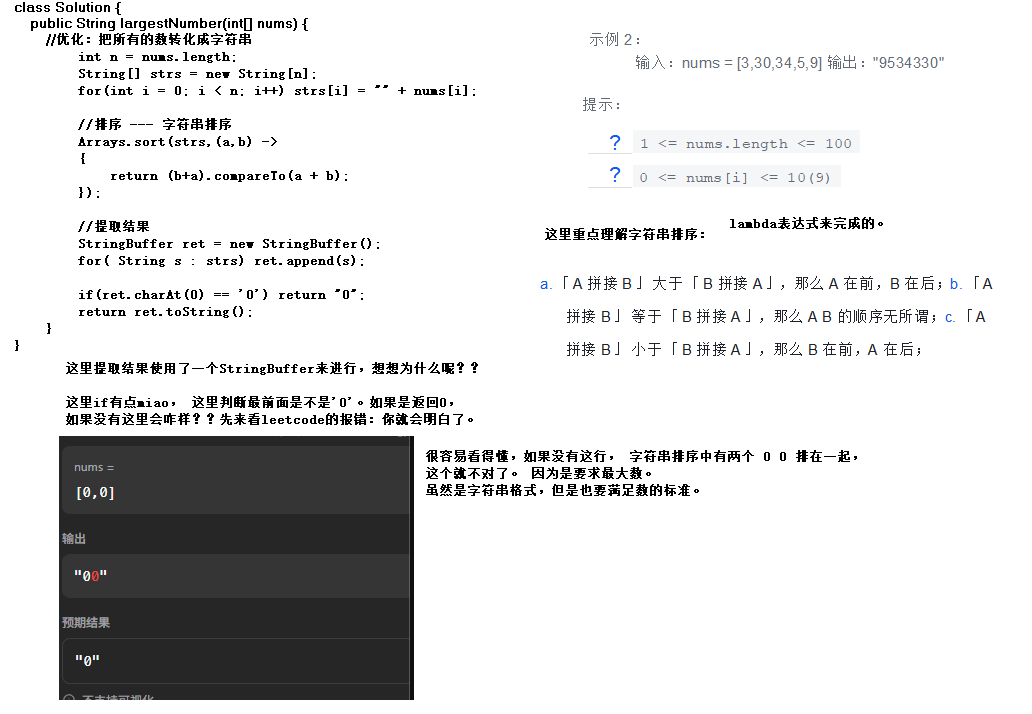
输入:nums = [3,30,34,5,9] 输出:"9534330"
提示:
| ◦ | 1 <= nums.length <= 100 | |
| ◦ |
| |
3. 解法(贪心):
可以先优化:
将所有的数字当成字符串处理,那么两个数字之间的拼接操作以及比较操作就会很方便。
贪心策略:
按照题目的要求,重新定义一个新的排序规则,然后排序即可。
排序规则:
a. 「A 拼接 B」 大于 「B 拼接 A」,那么 A 在前,B 在后;
b. 「A 拼接 B」 等于 「B 拼接 A」,那么 A B 的顺序无所谓;
c. 「A 拼接 B」 小于 「B 拼接 A」,那么 B 在前,A 在后;
Java算法代码:
class Solution {
public String largestNumber(int[] nums) {
//优化:把所有的数转化成字符串
int n = nums.length;
String[] strs = new String[n];
for(int i = 0; i < n; i++) strs[i] = "" + nums[i];
//排序 --- 字符串排序
Arrays.sort(strs,(a,b) ->
{
return (b+a).compareTo(a + b);
});
//提取结果
StringBuffer ret = new StringBuffer();
for( String s : strs) ret.append(s);
if(ret.charAt(0) == '0') return "0";
return ret.toString();
}
}运行结果:
贪心思想:
细节补充:读者,读完前面应该还是没有找到贪心算法,贪在哪里。
先要知道,得了解Arrays.sort,以及lambda表达式。
这里有排序和比较逻辑
这里笔者对代码进行改版:
class Solution {
public String largestNumber(int[] nums) {
// 1. 将整数转换为字符串数组
int n = nums.length;
String[] strs = new String[n];
for (int i = 0; i < n; i++) {
strs[i] = String.valueOf(nums[i]);
}
// 2. 手动实现冒泡排序,使用自定义比较规则
for (int i = 0; i < n - 1; i++) {
for (int j = 0; j < n - 1 - i; j++) {
String a = strs[j];
String b = strs[j + 1];
// 比较 (b + a) 和 (a + b)
if ((b + a).compareTo(a + b) > 0) {
// 如果 b 应排在 a 之前,交换
String temp = strs[j];
strs[j] = strs[j + 1];
strs[j + 1] = temp;
}
}
}
// 3. 拼接结果
StringBuilder ret = new StringBuilder();
for (String s : strs) {
ret.append(s);
}
// 4. 处理前导零
if (ret.charAt(0) == '0' && ret.length() > 1) {
return "0";
}
return ret.toString();
}
}这里笔者使用了,冒泡排序,来看看。
注意,这里的排序规则是,和我们正常对一组数来进行大小排序不一样。
这里只有排序规则不一样(AB 和BA的大小关系来进行的)。
所以这里的贪心呢??
贪心算法的核心
a. 什么是贪心算法?
- 贪心算法(Greedy Algorithm)是一种通过局部最优选择来期望获得全局最优解的算法。
- 特点:
- 局部最优:在每一步选择当前看起来最好的方案。
- 无回溯:不撤销之前的选择,依赖局部决策的累积效应。
- 适用性:需要在问题中证明局部最优可以导致全局最优。
b. 本题的贪心策略
- 问题分解:将最大数字构造问题分解为对字符串数组的排序问题。
- 局部最优选择:在每次比较两个字符串 a 和 b 时,选择使 b + a 字典序更大的排列(即 b 排在 a 之前),因为这可能导致最终拼接结果更大。
- 全局最优目标:通过这种排序规则,确保拼接后的数字字符串最大。
贪心体现:
- 每次比较时,选择 b + a > a + b 的顺序,相当于在当前局部位置优先选择“拼接后更大的结果”。
- 这种选择是局部的,不考虑后续的排列,只关注当前两个字符串的拼接效果。

贪心还有个最重要的一步,是要证明贪心策略的正确性(这里笔者暂时跳过)。
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








