题目描述
某市的M公园中有一个近乎圆形的湖,有100个主要景点分布在湖边,为了方便游客,公园在一些景点之间开设了直通的摩托飞艇摆渡的项目一来减少游客在景点到景点之间所花的时间,二来也可以让游客体验一下惊险刺激的摩托飞艇。果然摩托飞艇摆渡项目大为成功,为了充分满足游客需要,摆渡线路越来越多。不料随着线路的增加,危险性也随之增加。如果两个摆渡线路之间有交叉(如上图),在这两个线路上的飞艇一旦发生碰撞,后果将不堪设想。
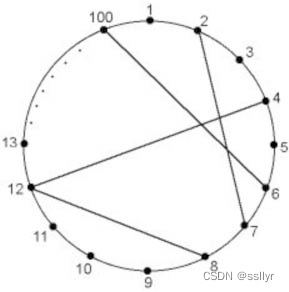
公园的管理层近日做出决定,本着安全第一的原则,在这个湖上取消一些线路,使剩下的任意两条线路在行驶阶段(即不考虑码头)不交叉。同时,考虑到经济效益,他们要求被取消的线路数最小,即保留尽量多的线路。他们希望你能够帮助他们算一算最多可以保留多少条线路。
分析
环形DP -> 展开成线,长度*2
先用邻接矩阵处理出哪两个连通
设
f
[
i
]
[
j
]
f[i][j]
f[i][j] 表示在区间
[
i
,
j
]
[i,j]
[i,j] 中的最多的线路数量,枚举长度,开头,中转点。
对于切分的小区间内,有转移
f
[
i
]
[
j
]
=
m
a
x
(
f
[
i
]
[
j
]
,
f
[
i
]
[
k
]
+
f
[
k
]
[
j
]
)
f[i][j]=max(f[i][j],f[i][k]+f[k][j])
f[i][j]=max(f[i][j],f[i][k]+f[k][j])
因为
(
i
,
j
)
(i,j)
(i,j) 可能有连线,且与区间内部的都不相交,所以有连线就+1。
最后的答案就是每个长度为100的区间的最大答案值。
上代码
#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
int n,ans,f[210][210],a[210][210];
int main()
{
cin>>n;
for(int i=1;i<=n;i++)
{
int x,y;
cin>>x>>y;
if(x>y) swap(x,y);
a[x][y]=a[x+100][y+100]=1;
}
for(int len=1;len<=100;len++)
{
for(int i=1;i+len-1<=200;i++)
{
int j=i+len-1;
for(int k=i;k<=j;k++)
{
f[i][j]=max(f[i][j],f[i][k]+f[k][j]);
}
f[i][j]+=a[i][j];
}
}
for(int i=1;i<=100;i++)
{
ans=max(ans,f[i][i+100-1]);
}
cout<<ans;
return 0;
}
























 124
124

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








