文章里定义了sparse coding(一下简称SC)的目的是:训练一组很少的基向量,对它们带权重地线性组合。然后这些基向量可以捕捉输入数据的high-level patterns(features)。 SC的特别之处:利用没有标记的输入数据,可以发现基函数。
本文提出了一种有效找到sparse codes算法:迭代的解决两个凸优化问题:一个L1 regularized least squares problem,一个L2 constrained least square problem。在解决L1 least squares problem to learn coefficients;Lagrange dual method for the L2 constrained least squares probl;em to learnn the bases for any sparsity penalty function。
优点是:速度快,可以处理比以前大的数据。在natural images上做了实验,可以学习over complete的基。
具体算法如下:
设输入图像信息为X,基为B,X是权重系数。认为重建误差
 符合0均值的高斯分布、且协方差为
符合0均值的高斯分布、且协方差为
 。设每个系数的先验分布为
。设每个系数的先验分布为
 ,其中beta是阐述,
,其中beta是阐述,
 是sparsity function.可以去不同的形式:
是sparsity function.可以去不同的形式:
 。
。
 符合0均值的高斯分布、且协方差为
符合0均值的高斯分布、且协方差为
 。设每个系数的先验分布为
。设每个系数的先验分布为
 ,其中beta是阐述,
,其中beta是阐述,
 是sparsity function.可以去不同的形式:
是sparsity function.可以去不同的形式:
 。
。
本文使用L1 penalty function.
假设了一个uniform prior on the bases以后,对基和系数的最大后验估计就是接下面这个优化问题
 。进一步写成下面的矩阵形式:
。进一步写成下面的矩阵形式:
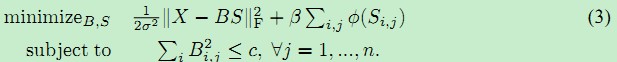 。
。
 。进一步写成下面的矩阵形式:
。进一步写成下面的矩阵形式:
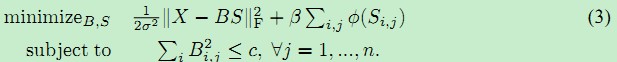 。
。
保持S不变时,B是convex的;保持B不变时,S是convex的。但不能同时convex。所以学习基B的优化问题是一个least squares problem with quadratic constraints。本文使用Lagrange dual方法来解这个问题,优于以前的gradient descent 和generic convex optimization solvers。
对于解决feature-sign search Alg.,不是很懂,写得很复杂,令基是固定的,后面好像怎么转化成解一个unconstrained
quadratic optimization problem (QP)。后面很复杂,就没看了。
P.S. 此文由代码 下下来了
























 7万+
7万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








