叶轮腔预旋系统新设计

一种用于高效增压和低功耗的叶轮腔预旋系统的新设计

1 引言

基于经典布雷顿循环的高涡轮进口温度长期以来被认为是满足更高推重比和更高效航空发动机需求的重要发展方向。在过去的70年中，压气机出口温度从600 K上升到1100 K，而涡轮进口温度则从1100 K升至2000 K。如何在极端服役条件下确保热端部件的长期使用现已成为一个难题。

作为空气系统的一部分，预旋系统可通过提高来自压气机的冷却空气静压来改善涡轮叶片的冷却效果。为降低相对速度和气流耗散，并减少供给涡轮叶片的冷却空气的相对总温，Meierhofer B 和 Franklin CJ [1]于1981年首次提出了预旋喷嘴。研究人员开展了预旋供气方法的研究，由此引入了预旋系统的概念。Dittmann [2]分析了盖板系统中压力、旋流比以及接收孔和喷嘴结构对流量系数的影响。Gang Zhao [3]提出了一种三维预旋喷嘴，以考虑喷嘴径向角度带来的优势。Roman A Didenko [4]研究了腔体宽度、预旋喷嘴位置和接收孔结构对系统流动特性、流量系数、绝热效率和温降的影响。Jianchao Zhang [5]基于数值与实验研究，揭示了径向预旋系统和轴向预旋系统的气动性能。通过实验和数值计算研究了部分预旋喷嘴通道关闭对预旋系统的质量流量和供气温度的影响[6]。Xiang Luo [7]基于腔内温度和努塞尔数分布的分析，揭示了高进口转子‐定子腔的传热特性。Gaowen Liu [8]通过理论分析提出了喷嘴出口处无量纲温降与旋流比之间的线性关系，该关系在预测值与数值结果之间表现出良好一致性。Menghua Jian [9]指出了压比和旋转雷诺数对典型盖板预旋系统中流动结构、无量纲质量流量和降温效果的影响。

本文所涉及的系统是一种典型的盖板预旋系统，可减少高温气流泄漏进入接收孔和旋转腔体的泄漏量[10]。J. W. Chew [11]通过理论分析和实验建立了一个基础模型，用于计算冷却空气输送温度，该模型与测量结果高度吻合。张荆州 [12] 通过分析腔体表面努塞尔数的分布，研究了旋转雷诺数对转子‐定子腔传热特性的影响。为了研究典型转子‐静子系统的流场和传热特性，罗旭等人 [13] 采用瞬态热致变色液晶技术测量了转子表面的温度和努塞尔数分布。

根据文献中的相关信息，阿尼什·库马尔·古普塔 [14], 首次考虑了带有叶轮腔的预旋系统，认为在腔体内采用叶轮结构可以提高压比并改善旋流比分布。田淑清 [15] 研究了普通旋转腔、叶轮腔以及带拉削槽的叶轮腔在气动性能上的对比。吴查尔斯 [16]研究了有无叶轮的预旋系统在旋流比和压力损失方面的差异，以改善流场特性和满足供气压力要求。张建超和王索芳 [17]提出了叶轮结构参数对降温特性及流动阻力特性的影响，包括叶片数量、长度、宽度和位置。陈凡 [18]得出了不同旋转雷诺数下叶轮宽度对总压系数的影响。

本文讨论的研究旨在揭示叶轮结构对叶轮腔预旋系统的影响，并推导出叶轮腔流场与系统性能参数（如功耗和压比）之间的关系。为了对叶轮盘腔预旋系统进行定量分析，应用叶轮机械原理[19]研究速度场与静压及绝对总焓变化曲线之间的函数关系。研究结果将有助于叶轮盘腔的优化设计以及燃气涡轮发动机预旋系统的工程应用。

2 物理模型

2.1 数值方法

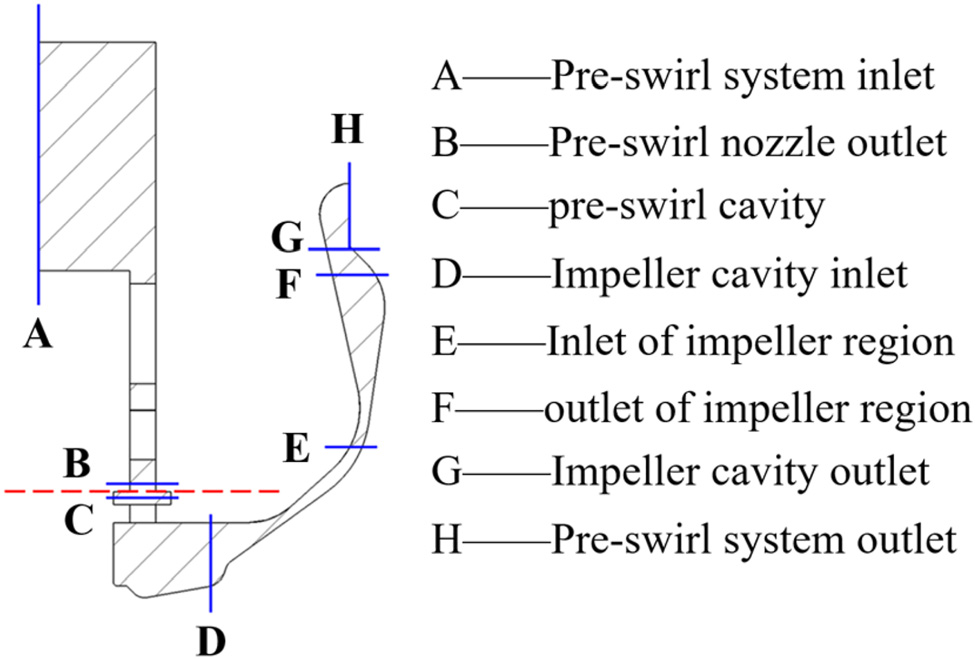
如图1所示，从实际航空发动机简化而来的叶轮腔预旋系统由稳压室、预旋喷嘴、预旋腔体、接收孔和叶轮腔组成。由于用于密封的气流较少，预旋中的泄漏流在叶轮腔中的涡流腔被忽略。在叶轮腔内，叶轮的设计旨在降低相对总温并提高腔体出口处的静压。

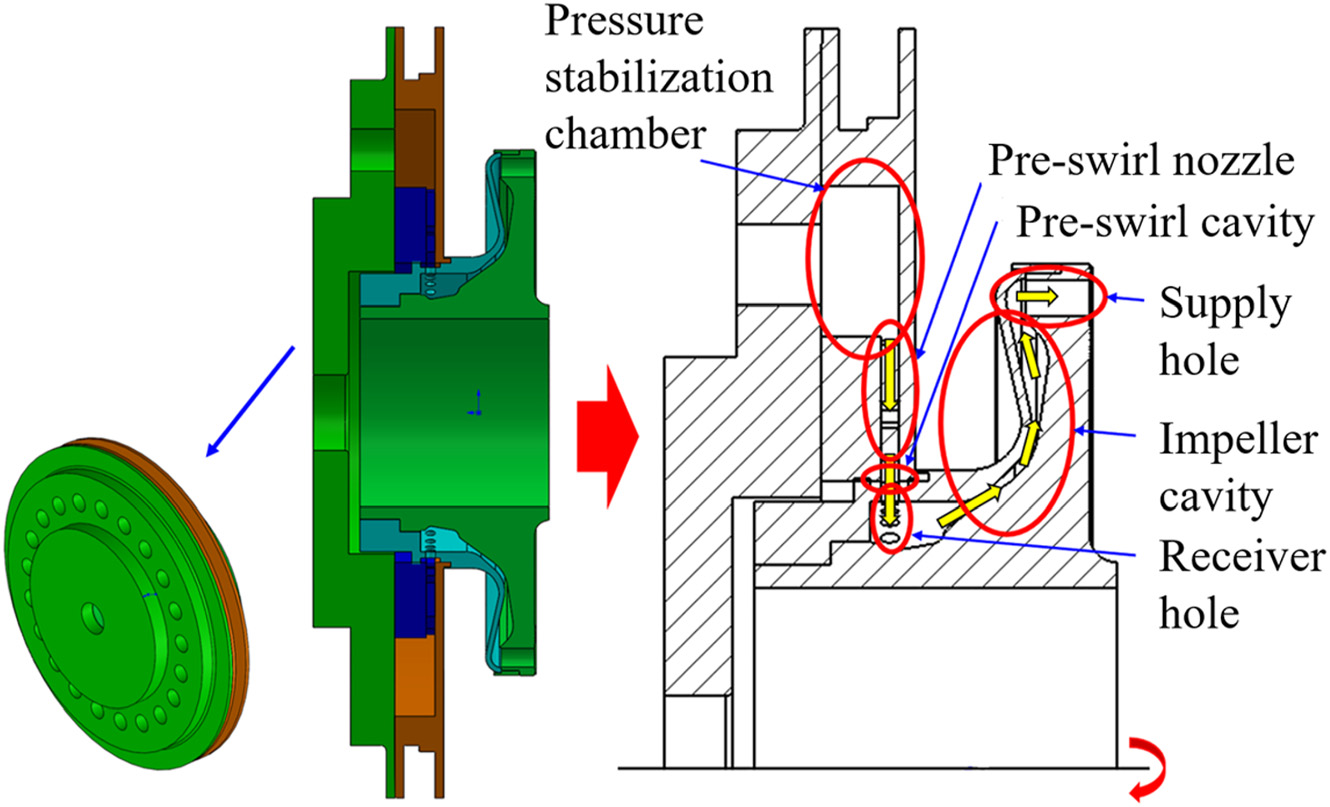
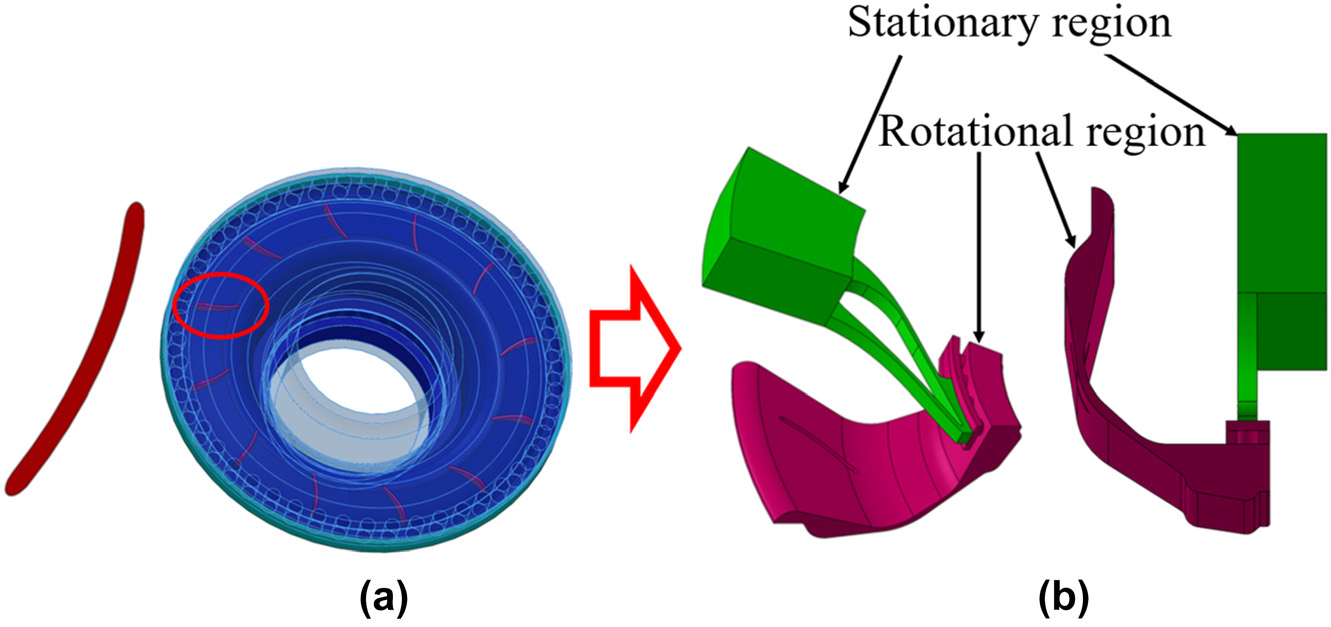
图2展示了带有叶轮的预旋系统中叶轮、叶轮流道以及内部流道的结构。内流道模型可分为静止域（绿色）和旋转域（红色）。静止域包含稳压室和预旋喷嘴，旋转域包括预旋腔、接收孔和叶轮盘腔。喷嘴中有21个预旋叶片，48个接收孔沿周向均匀分布。如图2所示，静止部分选取为1/21周期段，旋转部分选取为1/12周期段。

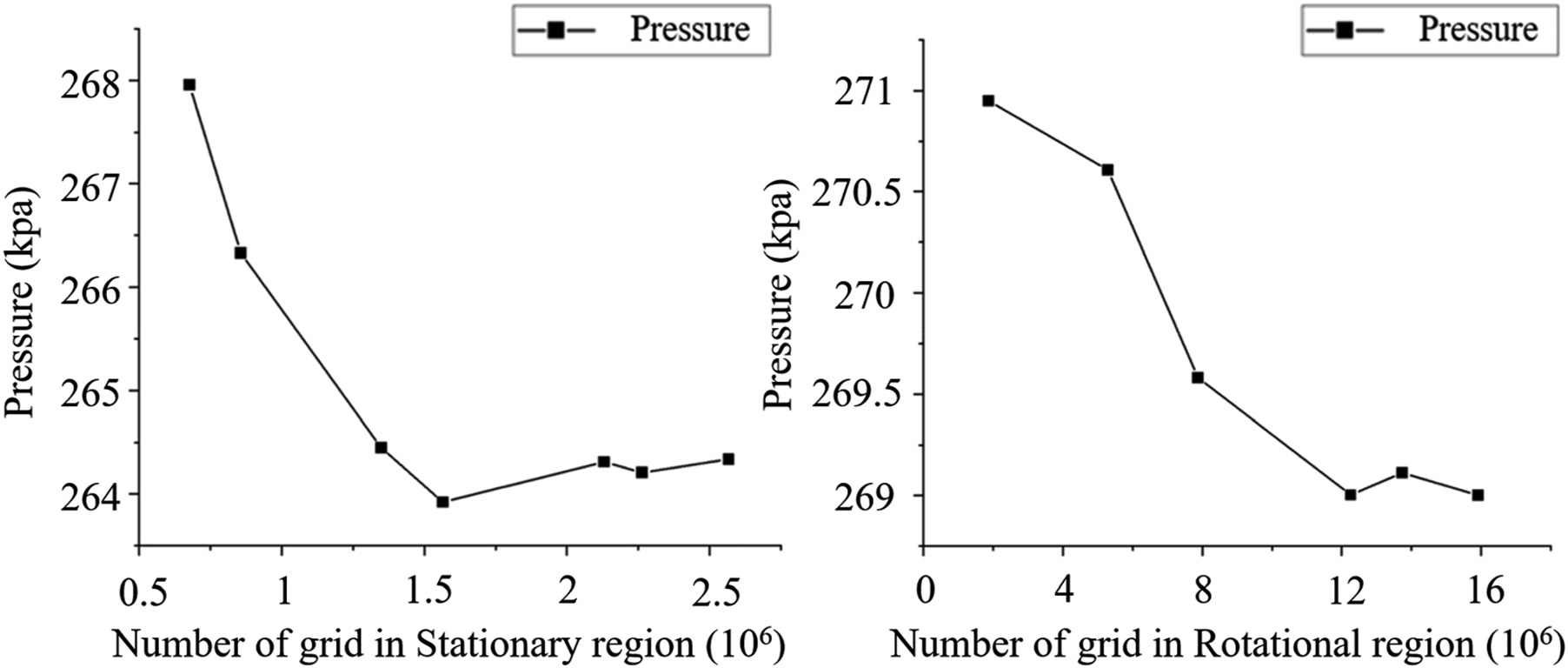
本研究中，ICEM CFD被应用于静止域和旋转域的网格划分。静止域采用结构化网格，而旋转域由于叶轮盘腔结构复杂多变，采用非结构化网格。网格独立性验证如图3所示。本研究基于y+的要求，对静止域和旋转域的网格独立性进行了验证。首先，分别确认了静止网格的独立性；其次，验证了在固定静止网格、改变旋转网格的情况下，组合网格以及旋转网格是否满足独立性要求。根据图3所示的曲线，静止域的网格数量为 2,264,016，旋转域的网格数量为13,781,104。根据张建超[6],、Riccardo Da Soghe[20]和Karnahl J[21],对湍流模型和参考系变换模型的研究，数值模拟中采用了标准k–ε模型和冻结转子模型，具体计算方程可参见CFX用户指南[22]。

2.2 叶轮腔体结构与气动边界条件

边界条件设置如表2所示。系统进口采用静压边界条件，系统出口采用质量流量边界条件。稳压室、预旋喷嘴、预旋腔和叶轮盘腔中的所有周期面均设置为旋转周期边界条件。预旋系统中所有壁面均设为绝热且无滑移。

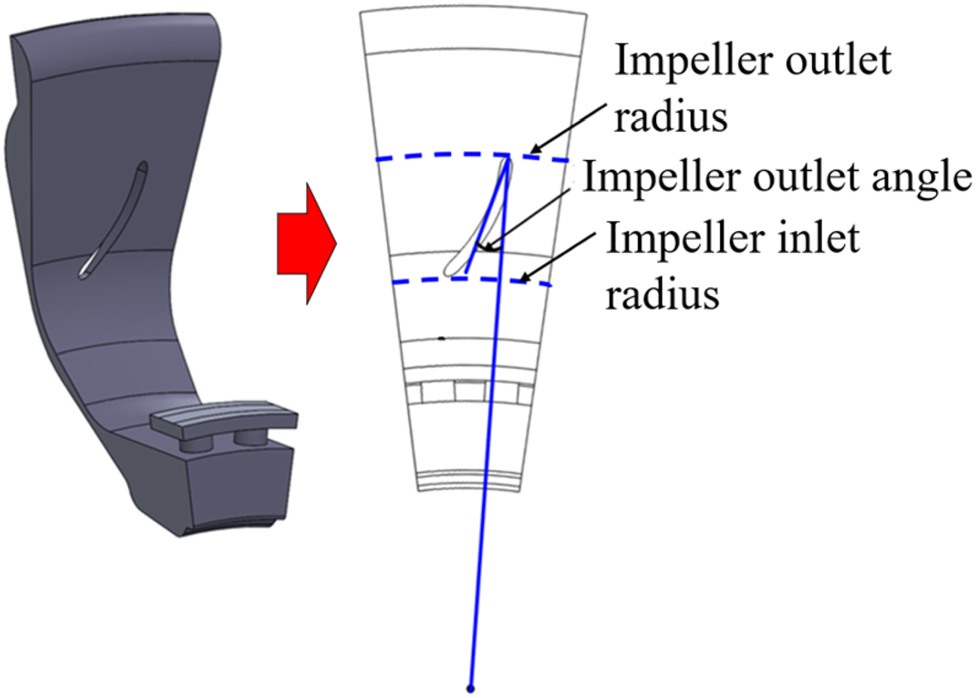
叶轮腔体的结构包含叶轮进口和出口的安装半径、叶轮出口的出口角度以及叶轮叶片数字以及叶轮安装位置的结构如表1所示。叶轮出口角度的示意图如图4所示。

叶轮	进口半径/mm	出口半径/mm	叶轮	进口半径/mm	出口半径/mm
叶轮1	80	100	叶轮8	100	130
叶轮2	90	110	叶轮9	100	133
叶轮3	100	120	叶轮10	80	120
叶轮4	110	130	叶轮11	90	130
叶轮5	110	133	叶轮12	90	133
叶轮6	80	110	叶轮13	80	130
叶轮7	90	120	叶轮14	80	133

表1：叶轮结构

条件	进口静压/千帕	进口总压/千帕	出口流量/(克/秒)	旋转转速/(转/分钟)
工况a	312.8	447.5	145	15,828
工况b	312.8	447.5	145	20,000
工况c	312.8	447.5	200	15,828

表2：气动边界条件

3 理论分析

基于叶轮机械原理，可利用特征来研究叶轮腔的流场叶轮腔特征位置处的参数。预旋系统中特征位置的详细信息可参见图5。

根据叶片机械原理，叶轮功可表示如下。

$$
W_{D-G} = h^ _{abs,G} - h^ {abs,D} = \mu_F c {u,F} \omega r_F - c_{u,E} \omega r_E = \mu_F c_{u,G} \omega r_G - c_{u,D} \omega r_D \quad (1)
$$

其中 $\mu_F$为叶轮出口的滑移因子，其表达式见公式(2)。$c_{u,E}$和$c_{u,F}$分别为叶轮进口和叶轮出口处的绝对周向速度（米/秒）。$\omega$为叶轮腔体的角速度（弧度/秒）。$c_{u\infty,F}$为无限多叶片叶轮在叶轮出口处的绝对周向速度（米/秒）。

$$
\mu_F = \frac{c_{u,F}}{c_{u\infty,F}} \quad (2)
$$

根据叶轮机械原理[19]，叶轮腔的压比可表示如下。

$$
\ln\left(\frac{p_G}{p_D}\right) = \ln\left(\frac{p_G}{p_D}\right) {work} + \ln\left(\frac{p_G}{p_D}\right) {velocity} + \ln\left(\frac{p_G}{p_D}\right) {dissipation} = \frac{W {D-G}}{RT} - \frac{c^2_D - c^2_G}{2RT} - \frac{L_{f, D-G}}{RT} \quad (3)
$$

其中，$T$为叶轮腔体的平均温度（开尔文），$L_{f, D-G}$为叶轮腔体的耗散（焦耳）。此外，根据开口系统的熵方程，耗散可表示如下。

$$
L_{f, D-G} = T\left(C_p \ln\frac{T_G}{T_D} - R_g \ln\frac{p_G}{p_D}\right) \quad (4)
$$

系统压力比可以通过将公式(4)代入公式(3)得到，如公式(5)所示。

$$
\pi = \frac{p_{pH}}{p_A} = p_{pAD} \cdot \exp\left(\frac{W_{D-G}}{RT} - \frac{c^2_D - c^2_G}{2RT} - \frac{T(C_p \ln \frac{T_G}{T_D} - R_g \ln \frac{p_G}{p_D})}{RT}\right) \cdot p_{pHG} \quad (5)
$$

在接收孔区域（特征位置C‐D），可通过动量矩定理计算区域功耗。叶轮腔入口处的绝对周向速度可根据腔体的旋流比和局部旋转速度获得。接收孔区域的功耗可表示如下。

$$
W_{C-D} = \omega(c_{u,D}r_D - c_{u,C}r_C) = \omega(\beta_D \omega r_D \cdot r_D - c_{u,C}r_C) \quad (6)
$$

其中，$\omega$为叶轮腔的角旋转速度；$\beta_D$为叶轮腔入口处的旋流比，即叶轮腔入口绝对周向速度与该处腔体局部转速之比；$c_{u,D}$、$r_D$分别为叶轮腔入口处的绝对周向速度和半径。

4 结果与讨论

4.1 叶轮进出口安装半径

如公式(1)所示，叶轮腔内的功耗与叶轮腔内的速度场、转速以及叶轮出口处的滑移因子有关。由图6所示的绝对速度曲线可知，叶轮结构的变化不会影响叶轮腔前的速度场（特征位置A‐D）。腔体进口（特征位置D）处的速度对功耗的影响可以忽略不计。

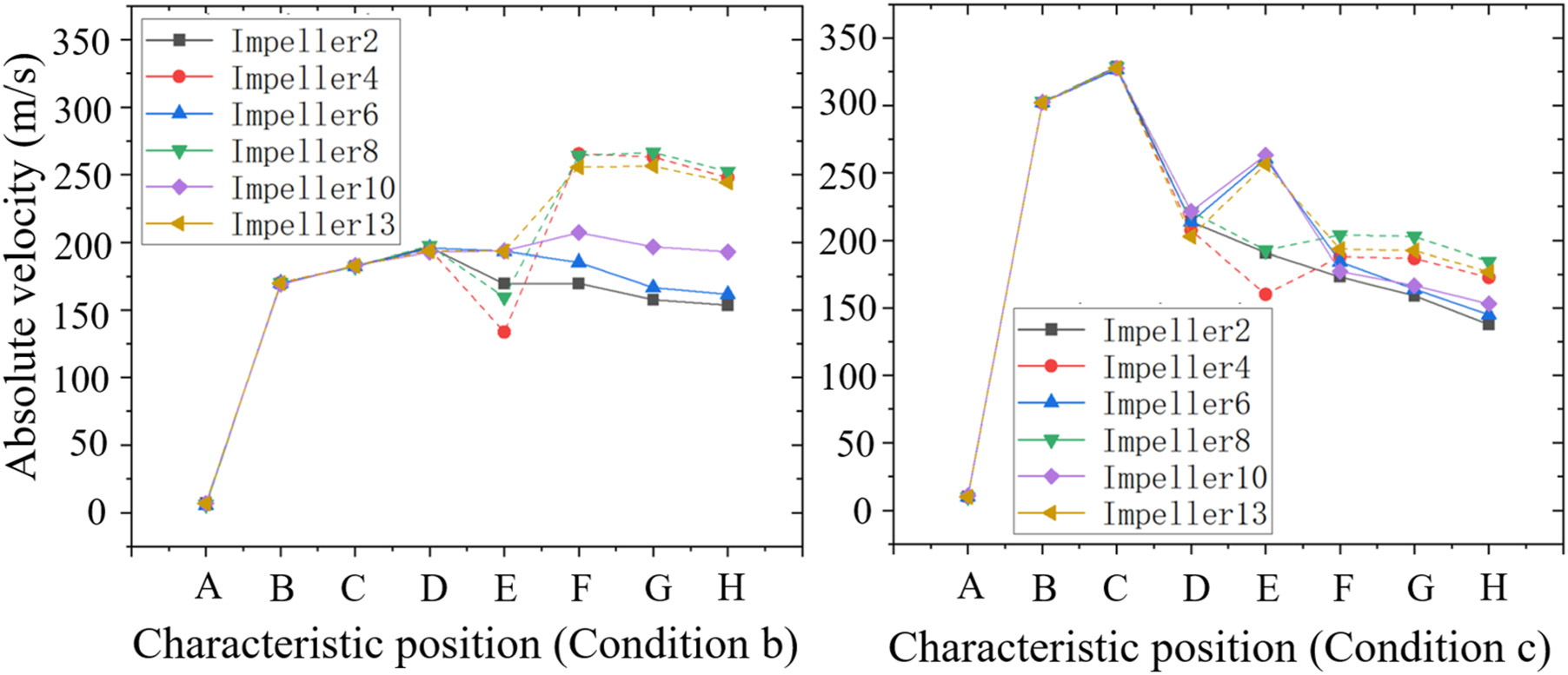
如图7所示，预旋喷嘴区域（特征位置A‐B）的区域功耗为零，因为该区域为静止区域。在预旋腔区域（特征位置B‐C），即旋转域与静止域交界处，由于局部旋转速度大于空气的周向速度，旋转部件对空气做功，导致总焓增加。然而，由于做功的范围和强度有限，局部功率交换非常小，可以忽略不计。在接收孔（特征位置C‐D）处，由于气流的周向速度大于接收孔的旋转速度，如图8所示，气流撞击壁面，通过绝对总焓的降低对接收孔做功。根据公式(6)，在叶轮腔入口转速和旋流比一定的情况下，预旋腔内绝对周向速度越小，区域功耗越大。此外，通过提高腔体的旋转速度或降低流量以减小$c_{u,C}$，可以减少气流对系统所做的冲击功。

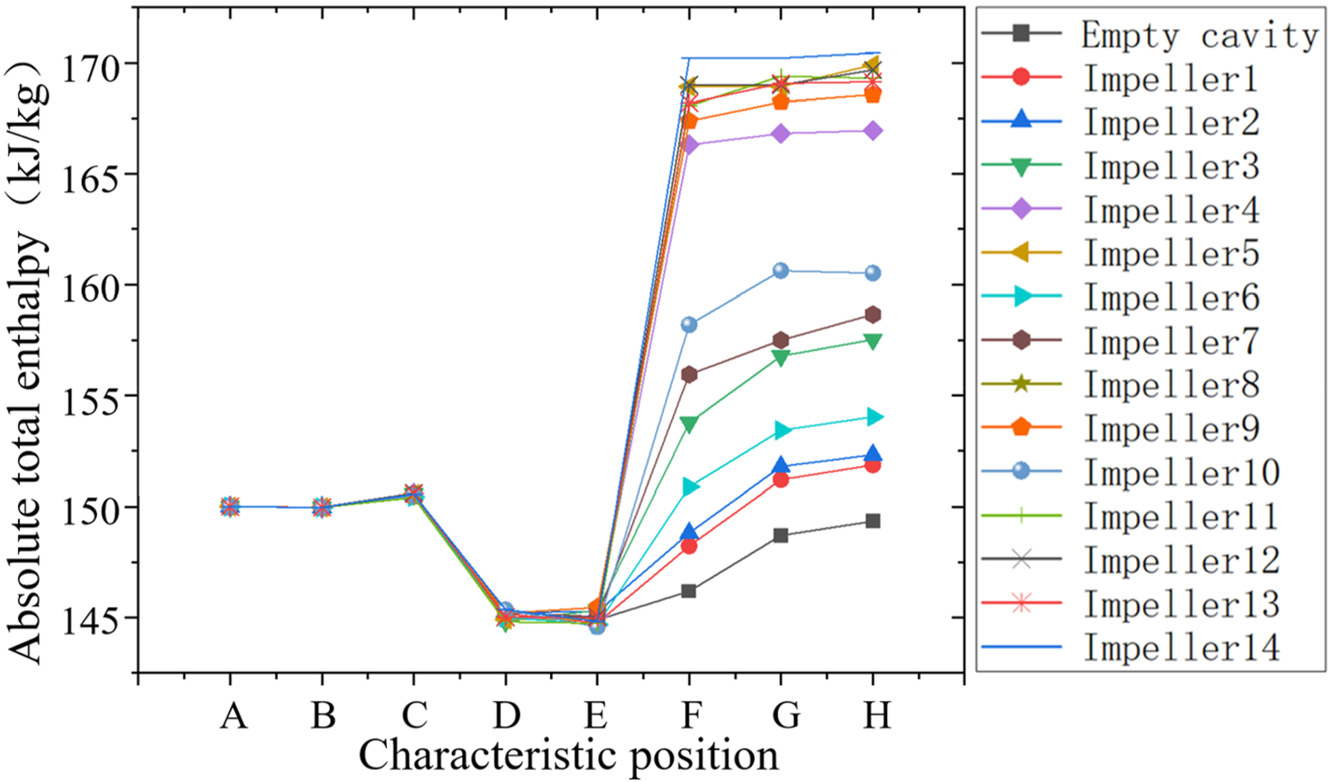
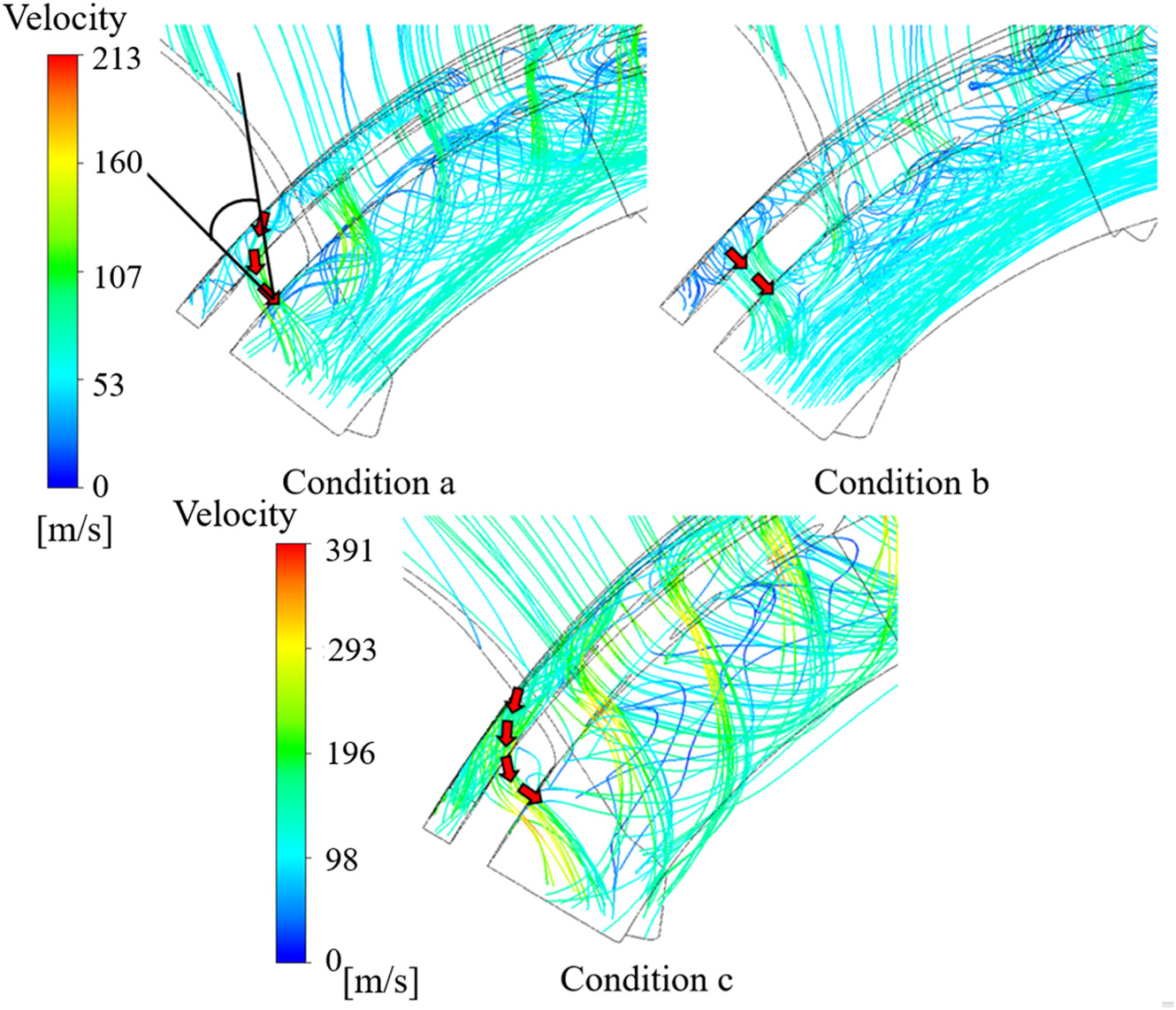
如图所示，不同叶轮结构的系统功耗差异主要体现在叶轮腔（特征位置D‐G）。随着叶轮出口安装半径$r_G$的增大，腔体出口C处的绝对周向速度$u,G$也随之增加，这可能导致叶轮腔内从系统到气流的功率交换增强，进而增加系统功耗。

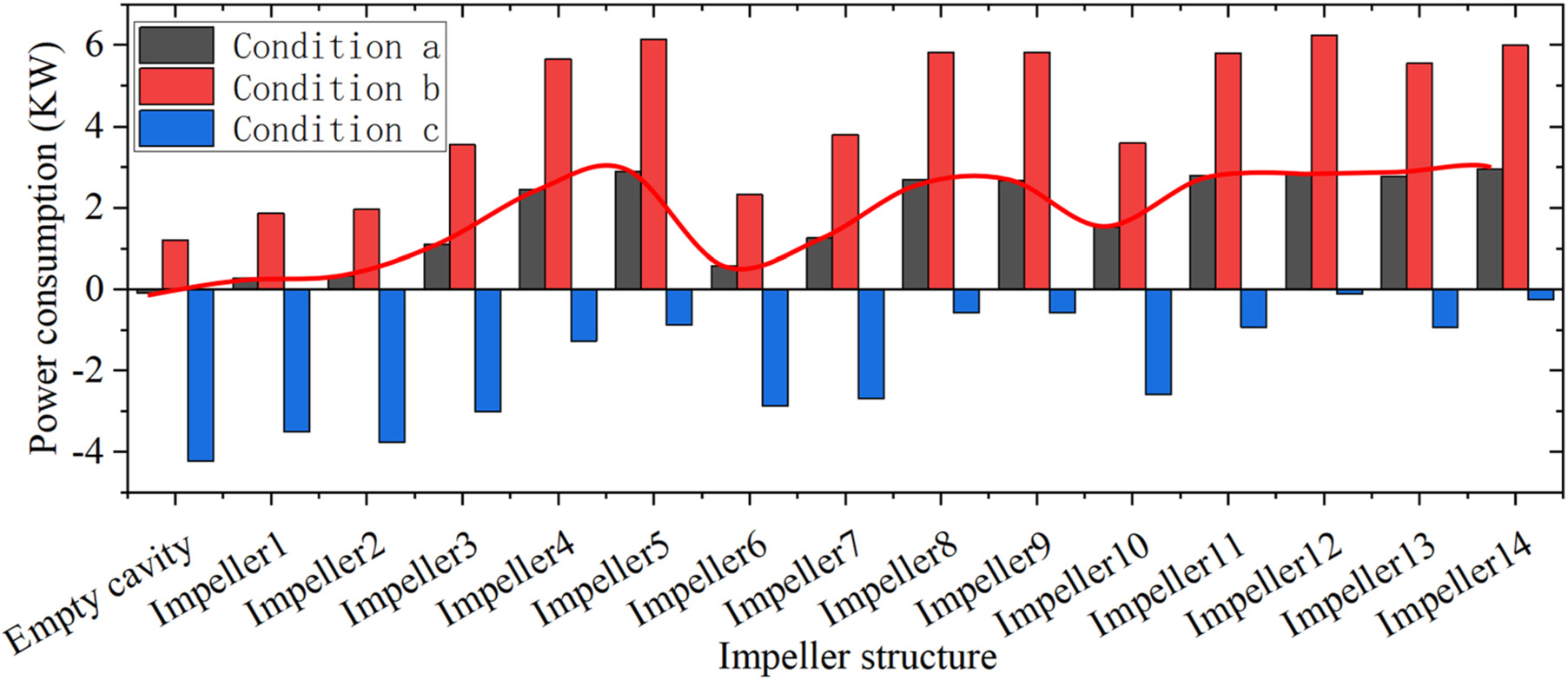
图9比较了不同叶轮下空腔预旋系统和叶轮腔预旋系统的功耗，叶轮的结构见表1。当气流在接收孔处传递给系统的功大于系统在叶轮腔内传递给气流的功时，功耗为负；否则系统功耗为正。在任何气动条件下，系统功耗随叶轮半径安装位置的增加而增加，并主要由叶轮出口安装位置决定。

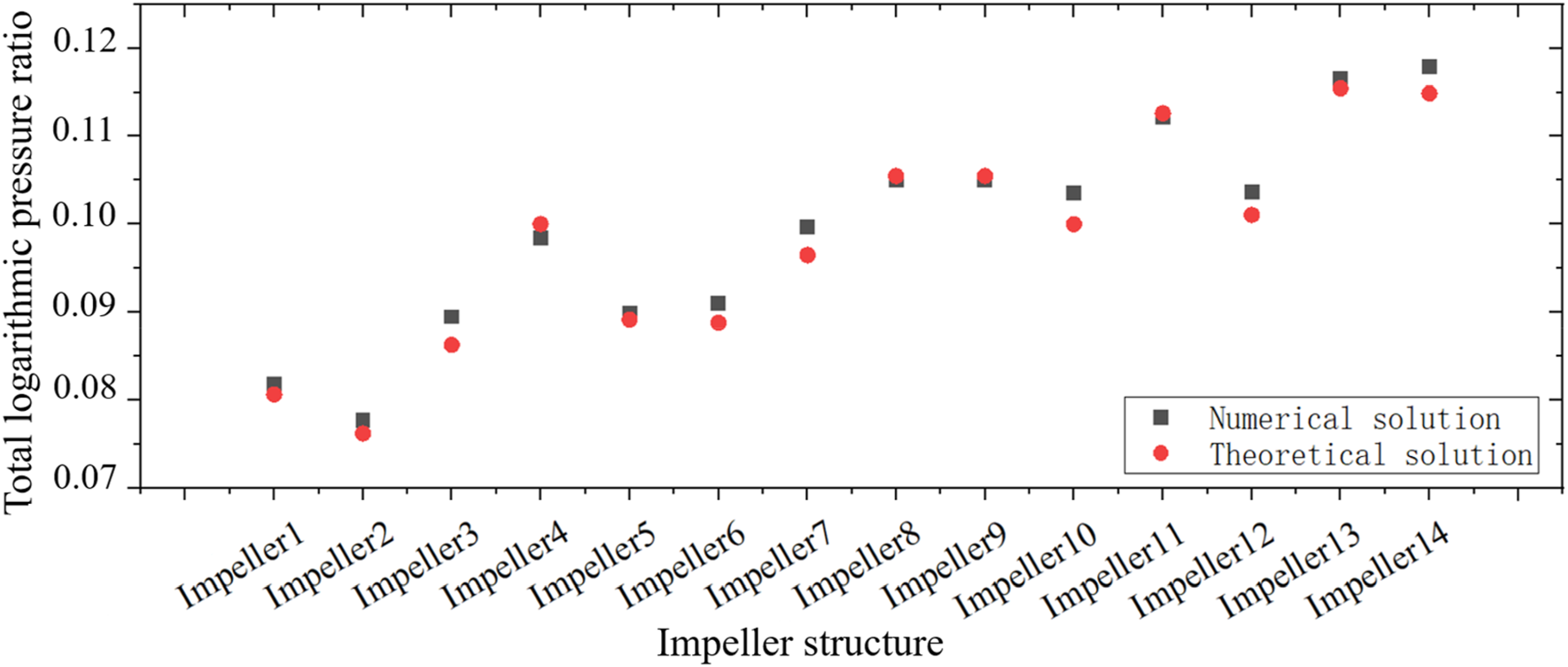
根据公式(3)和(5)，系统压力比可分为腔前区域压比、叶轮腔和系统出口三部分，叶轮腔内的静压可分为含速度的静压、叶轮腔和耗散。如图10所示，理论解与数值解之间的偏差小于3%，说明对数压比的计算是可信的。

叶轮结构对腔入口(A‐D)前区域压力变化的影响极小，可忽略不计，系统压力比的差异主要集中于叶轮腔区域(D‐G)和系统出口(G‐H)。图11(b)–(d)显示了叶轮腔内静压随叶轮功、速度及耗散影响的变化情况。根据公式(3)，静压与叶轮功关系与叶轮腔内的功耗呈正相关，且静压含速度的静压随着叶轮腔出口处绝对速度的增加而降低。

如图所示，静压与叶轮功关系随着叶轮腔出口处绝对周向速度的增加而增加，这是由增大$r_G$引起的。含速度的静压随着叶轮腔出口处绝对速度的增加而降低，这是由于高$r_G$的叶轮加速所致，但速度对静压的影响小于叶轮功的影响。耗散对静压的影响与叶轮功和速度相比太小，可忽略不计。因此，叶轮腔内的静压主要由叶轮功决定，且静压的增量随叶轮功的增加而增大叶轮功和叶轮出口安装半径。这意味着叶轮腔内的叶轮功是系统压力比的关键，通过增大$r_G$和叶轮功可以提高压比。

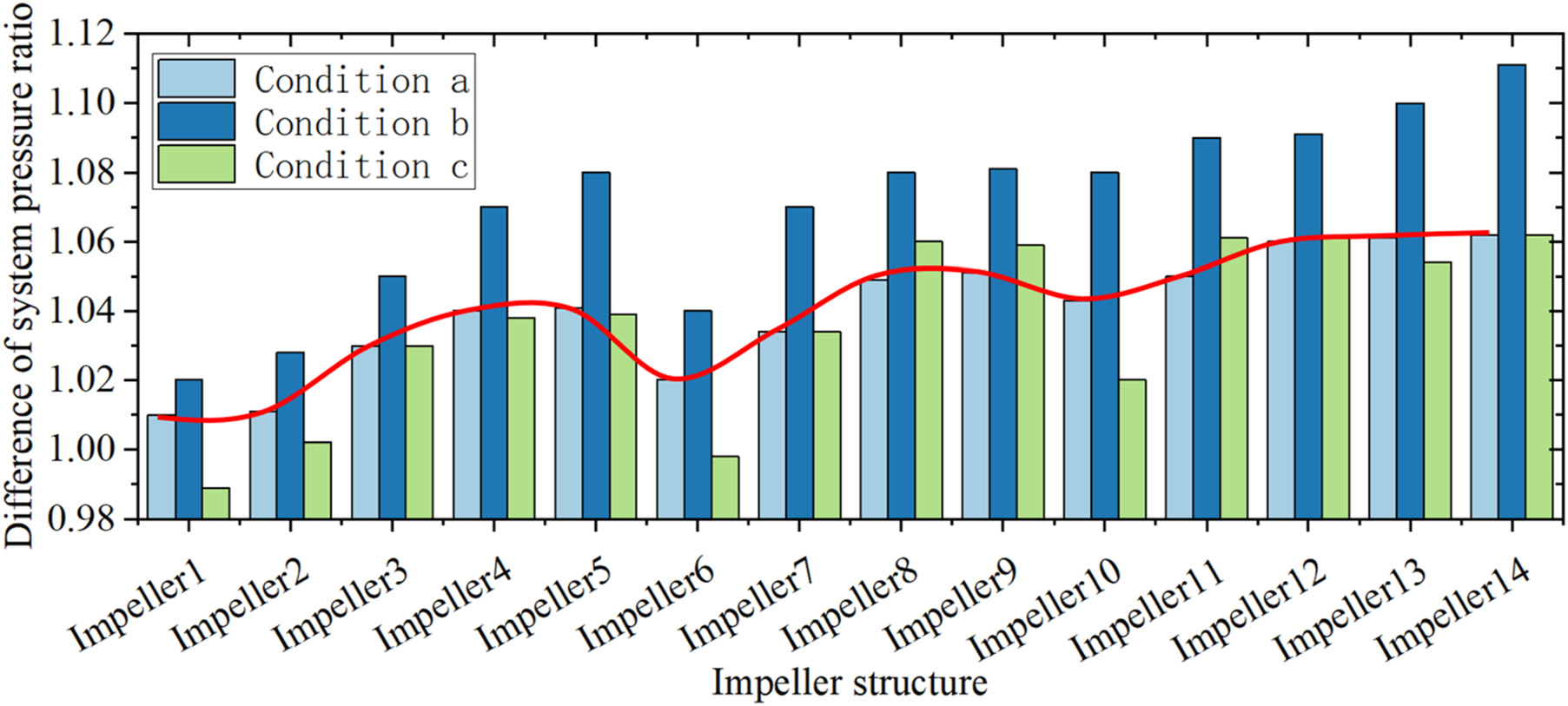
如图12中不同叶轮结构下系统压力比的对比所示，系统压力比的差异是指采用叶轮腔预旋系统与空腔预旋系统的压比之比。在相同条件下，系统压力比随着叶轮安装位置的增加而增大，这与上述分析一致。在条件b下，系统压力比的最大增幅可达11%。

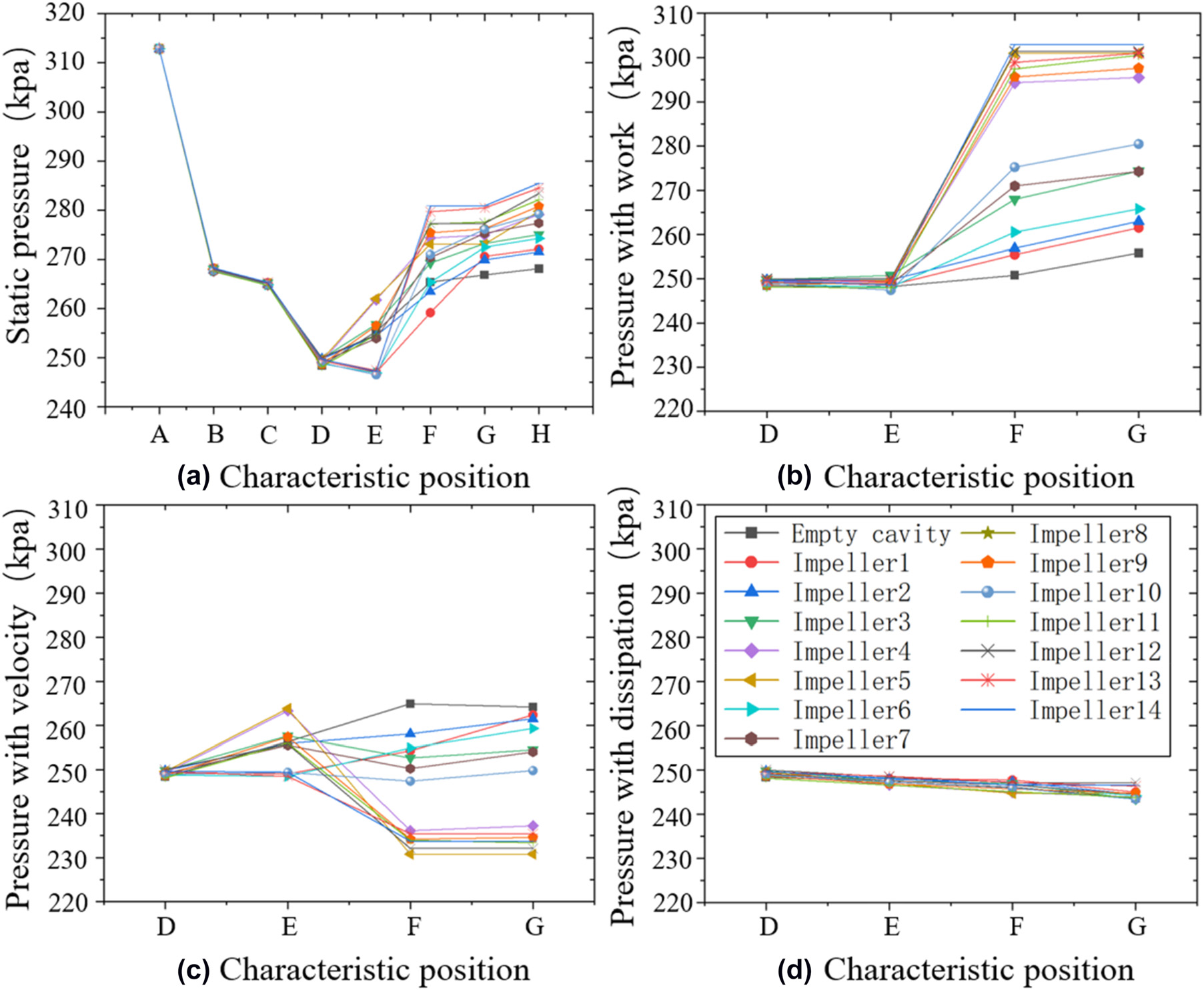静压、(b) 含叶轮功的静压、(c) 含速度的静压、(d) 含耗散的静压随不同叶轮结构的变化曲线。)

4.2 叶轮叶片数

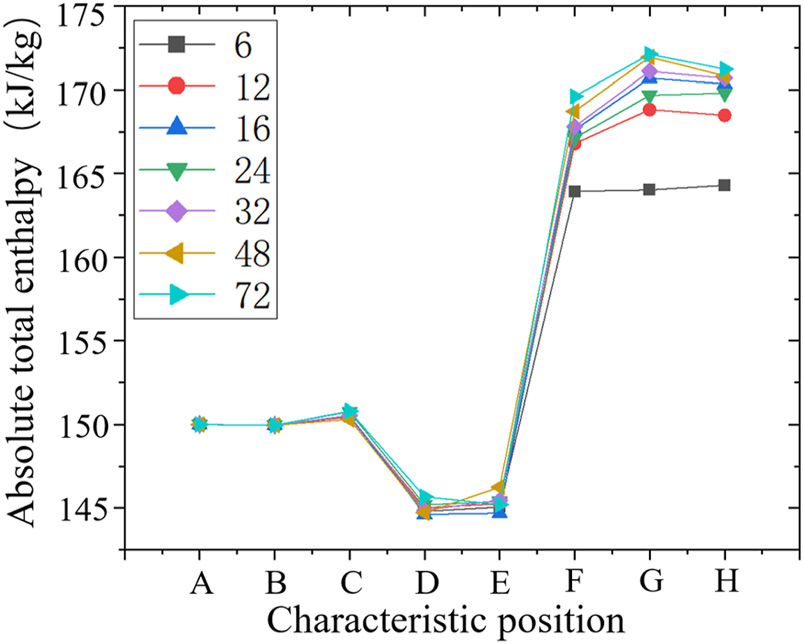
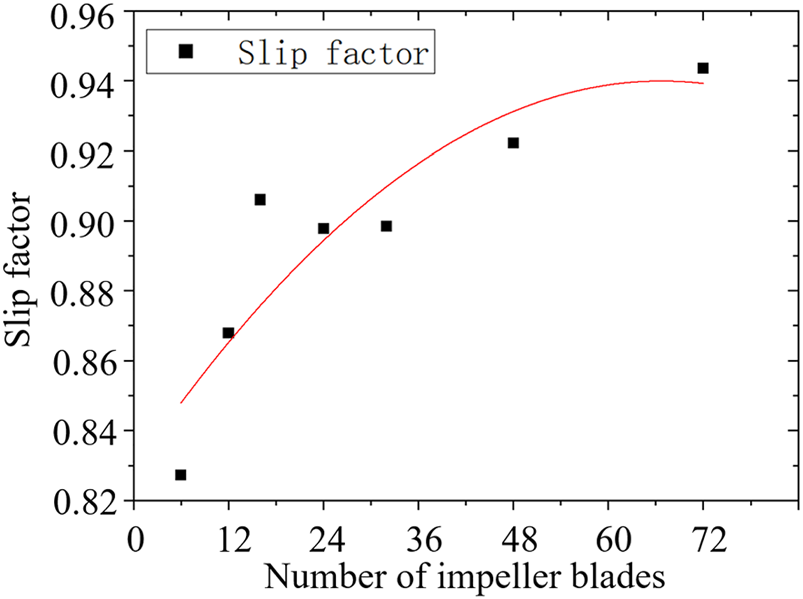
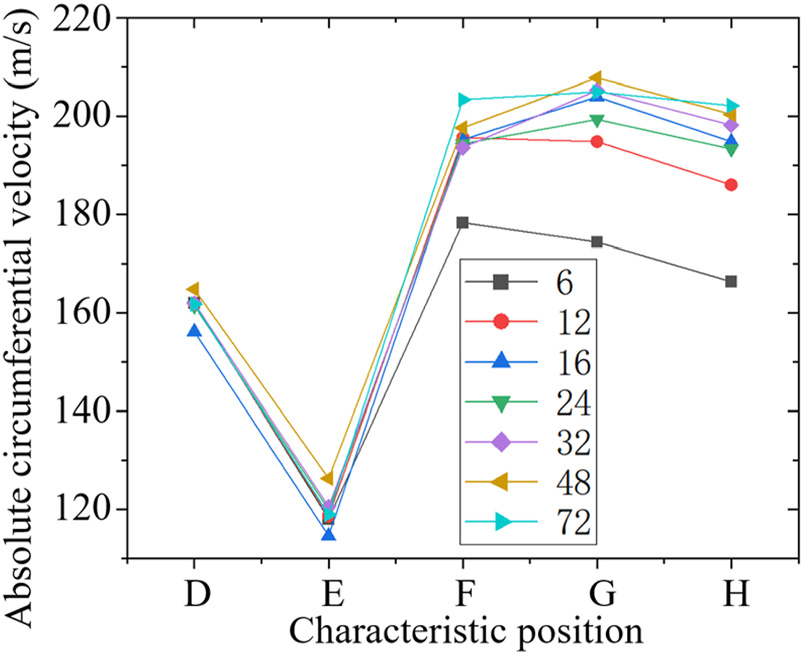
如图13所示，叶轮叶片数对绝对总焓的影响主要集中在叶轮腔内。根据公式(1)，区域功耗与滑移因子$\mu_F$呈正相关。从图14和图15可以看出，叶轮对腔内流场的控制力以及$\mu_F$随着叶轮叶片数的增加而增大。因此，功率预旋系统的功耗主要由叶轮腔内的功率交换决定，叶轮叶片数越高，腔体出口处的周向速度越高，系统功耗越大。

如图16所示，系统功耗随叶轮叶片数的增加而增加，这适用于任何叶轮结构。由于滑移因子随叶轮叶片数增加而增速减缓，随着叶轮叶片数量的增加，功耗的增长趋于稳定。

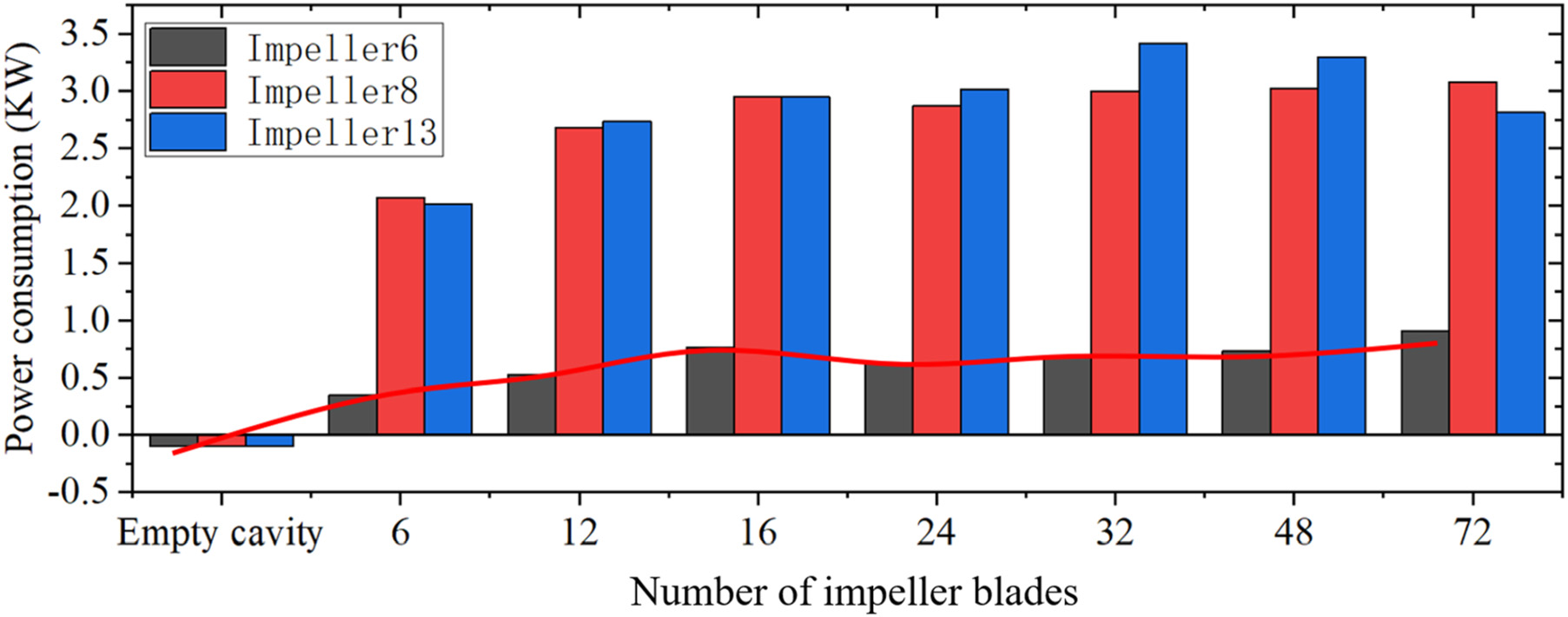
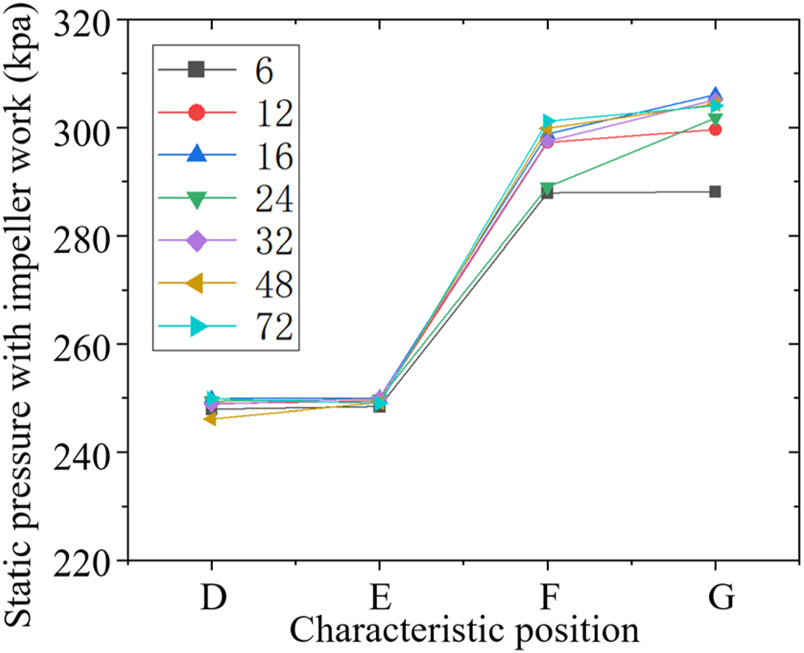
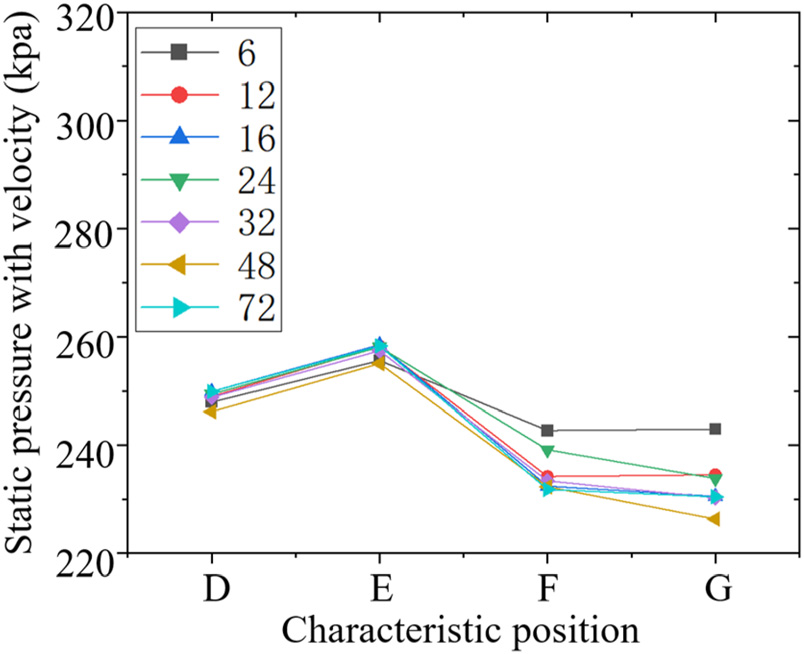
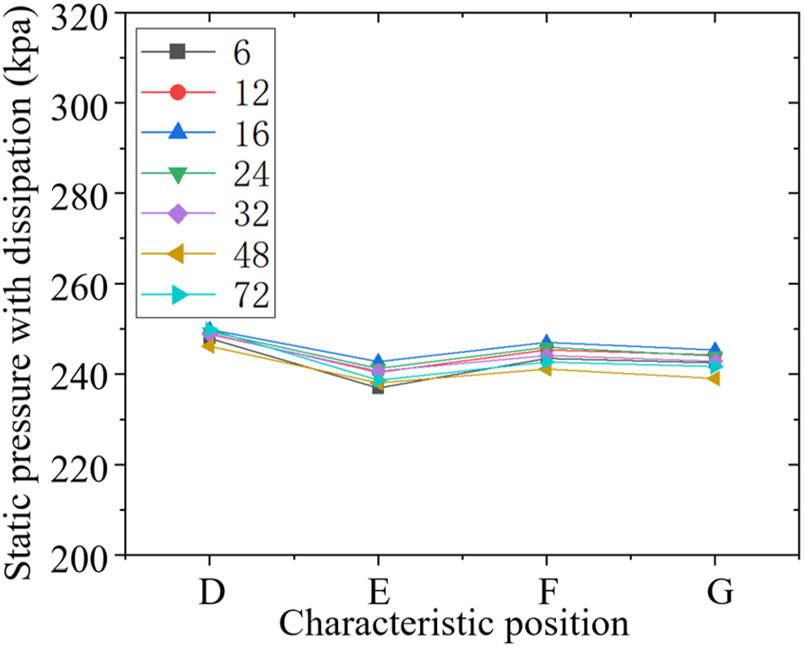
图17显示了不同叶轮叶片数量下静压差异主要集中于叶轮区域和系统出口处。静压与叶轮功、速度以及耗散的比较见图20–22。如图19所示，随着叶轮叶片数量的增加，腔体出口处的绝对速度增大。静压随叶轮功的增加幅度大于因速度引起的静压下降幅度，且二者均随着叶轮叶片数量的增加而增强。叶轮腔内静压的增量随着叶轮功的增加而减弱。系统出口处的静压变化主要受绝对速度和耗散的影响。如图18和图19所示，高叶轮叶片数量导致绝对速度大于叶轮叶片数较低时的速度，增加叶轮叶片数可有效抑制系统出口处的耗散强度，这可能最终促进静压的升高（图20–22）。

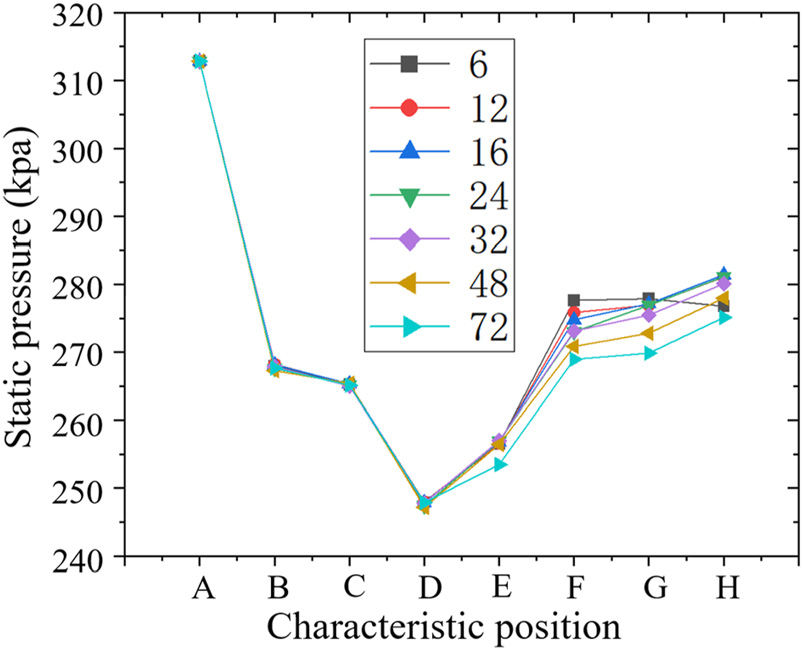
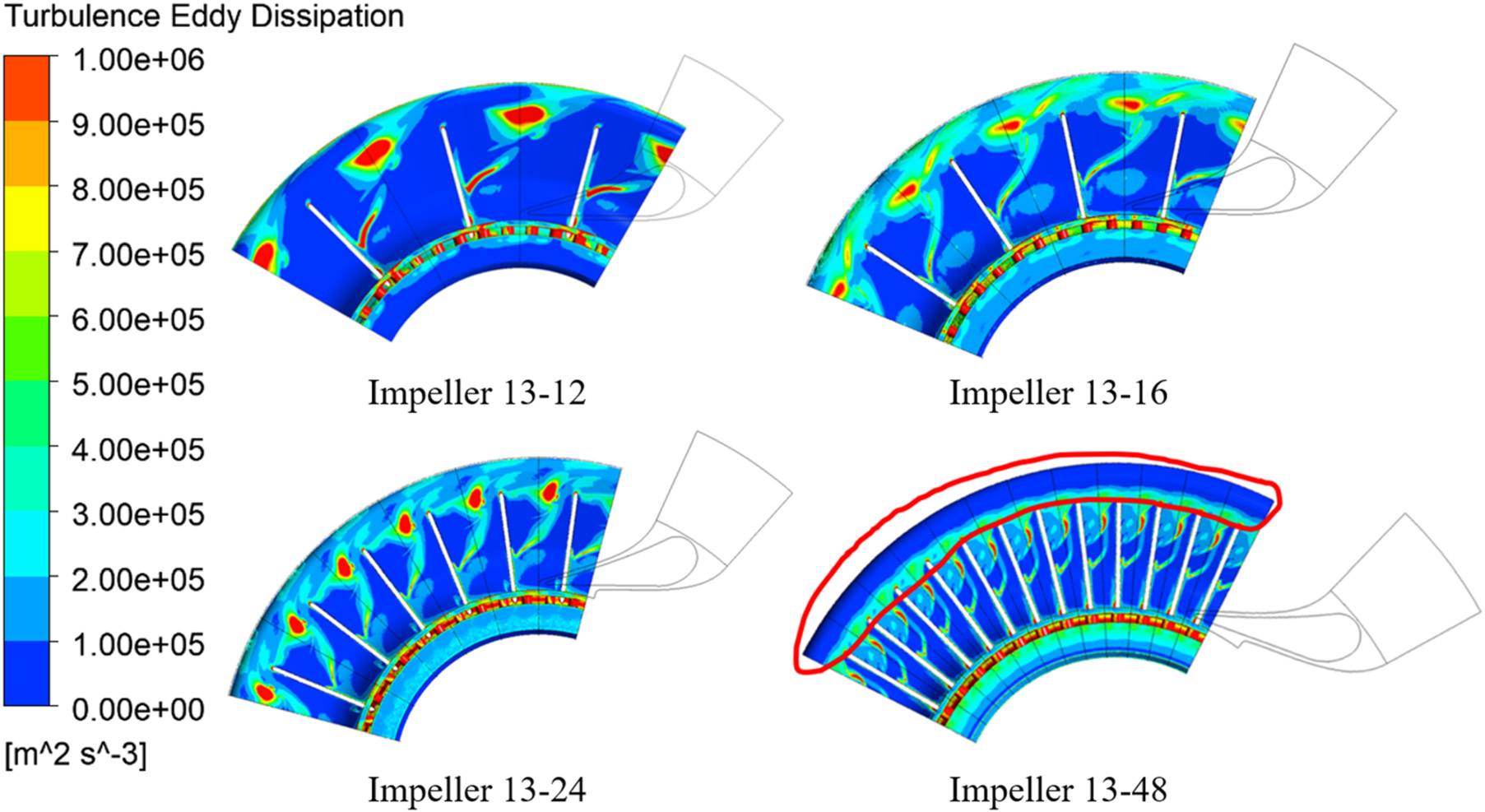
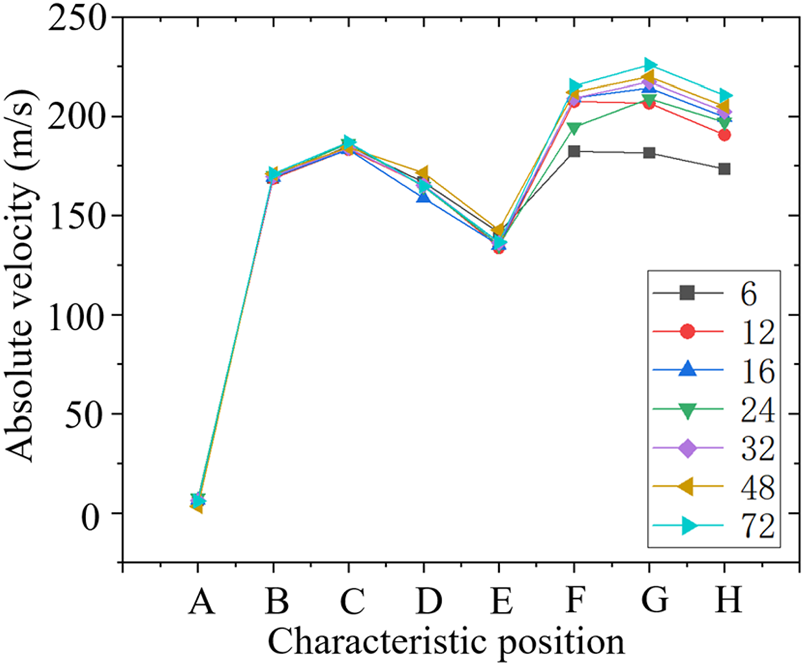
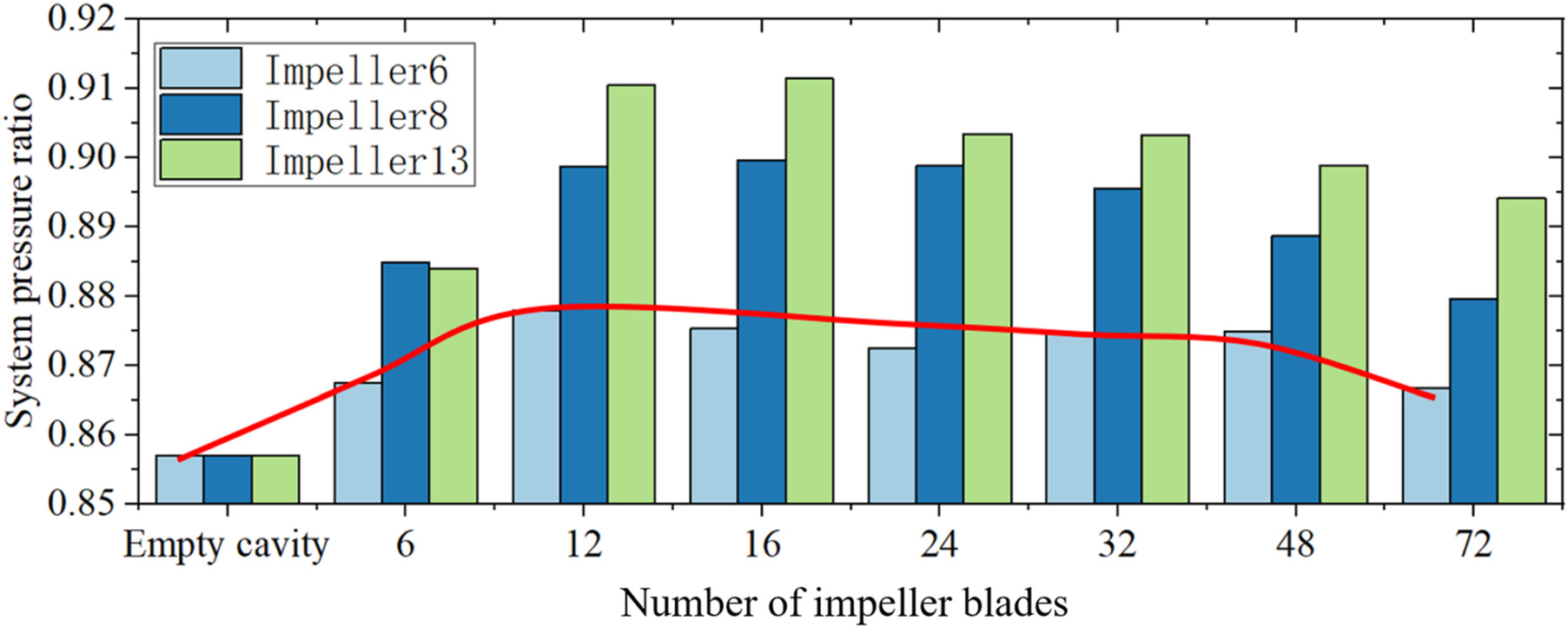
综上所述，随着叶轮叶片数量的增加，叶轮腔内静压的升高减弱，而系统出口处静压的升高增强。如图23所示，在叶轮腔与系统出口的相互作用下，不同叶轮叶片数量下的系统压力比呈波动状变化。然而，当叶轮叶片数量较低（如6片）时，由于系统出口处静压升高较小，系统压力比较平均值低；当叶轮叶片数量较高（如72片）时，由于叶轮腔内静压升高较小，系统压力比也低于平均值。

4.3 出口安装角

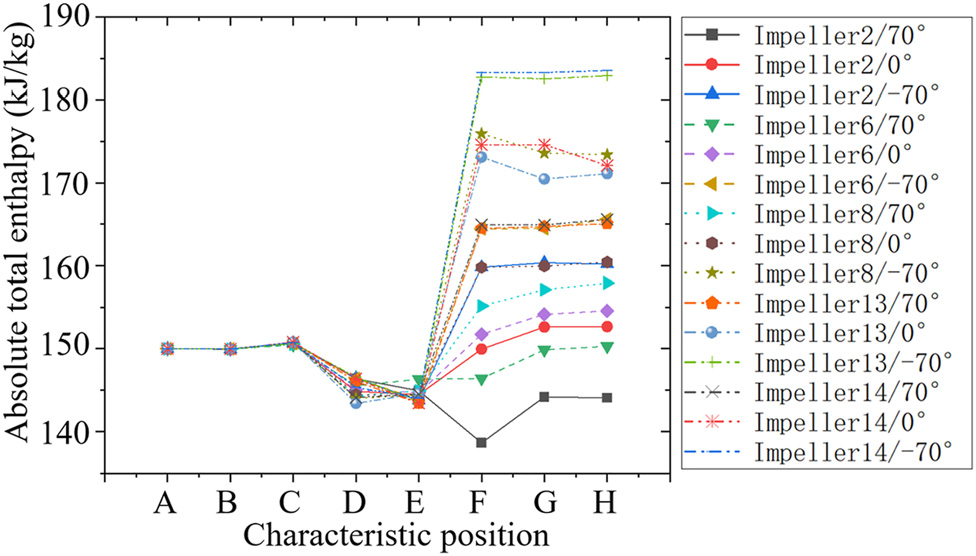
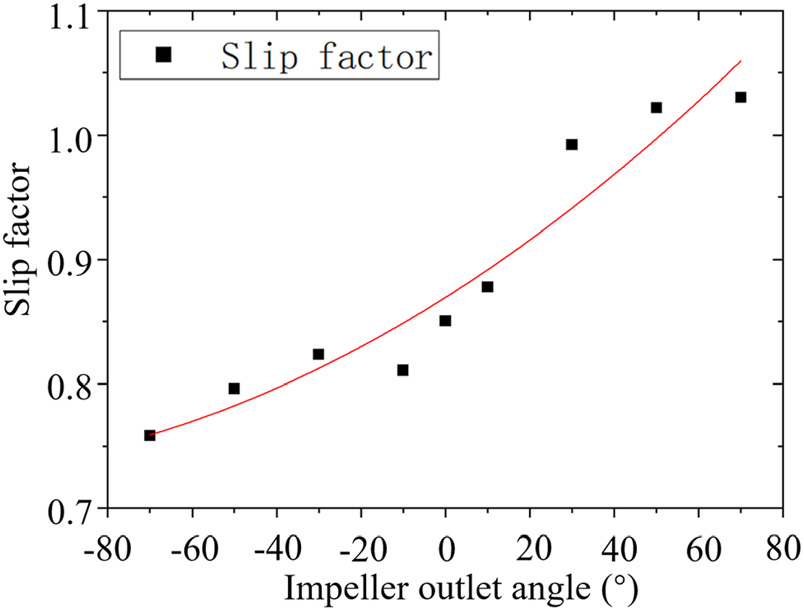
图24和图25展示了叶轮在不同出口角下总焓和绝对周向速度的曲线。叶轮出口角度的影响主要体现在叶轮腔内。叶轮出口处的绝对周向速度由无限叶轮叶片数对应的周向速度和滑移因子$\mu_F$决定。尽管如图26所示，滑移因子随叶轮出口角度的增大而增加，但绝对周向速度主要取决于无限叶轮叶片数对应的周向速度，该速度随出口安装角的增大而减小。从图25可以看出，绝对周向速度随着出口安装角的减小而增大。出口安装角越高，叶轮出口处的绝对周向速度越低，叶轮腔内的功耗也越低。此外，在图24中，对于叶轮2/70°，由于具有较高的叶轮出口角度和较小的出口安装半径，叶轮出口处的绝对周向速度低于叶轮进口处的速度。此时叶轮腔内的功耗为负值，气流对腔体做功。

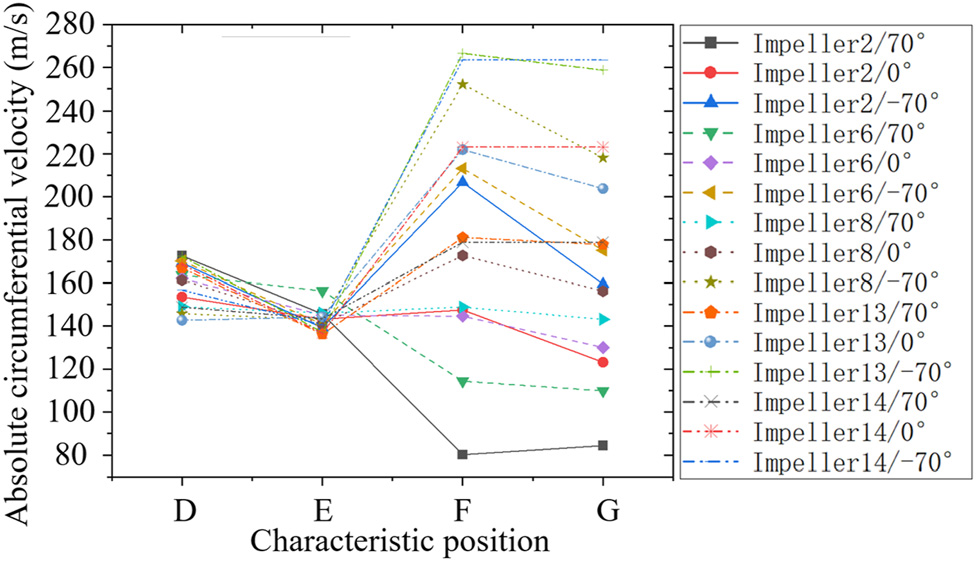
如图27所示，系统功耗随着出口角的减小而增加。对于相同的出口角，高出口安装半径的功耗始终大于低出口安装半径的功耗。高出口安装半径和低出口角的功耗远大于低出口安装半径和高出口角的功耗。

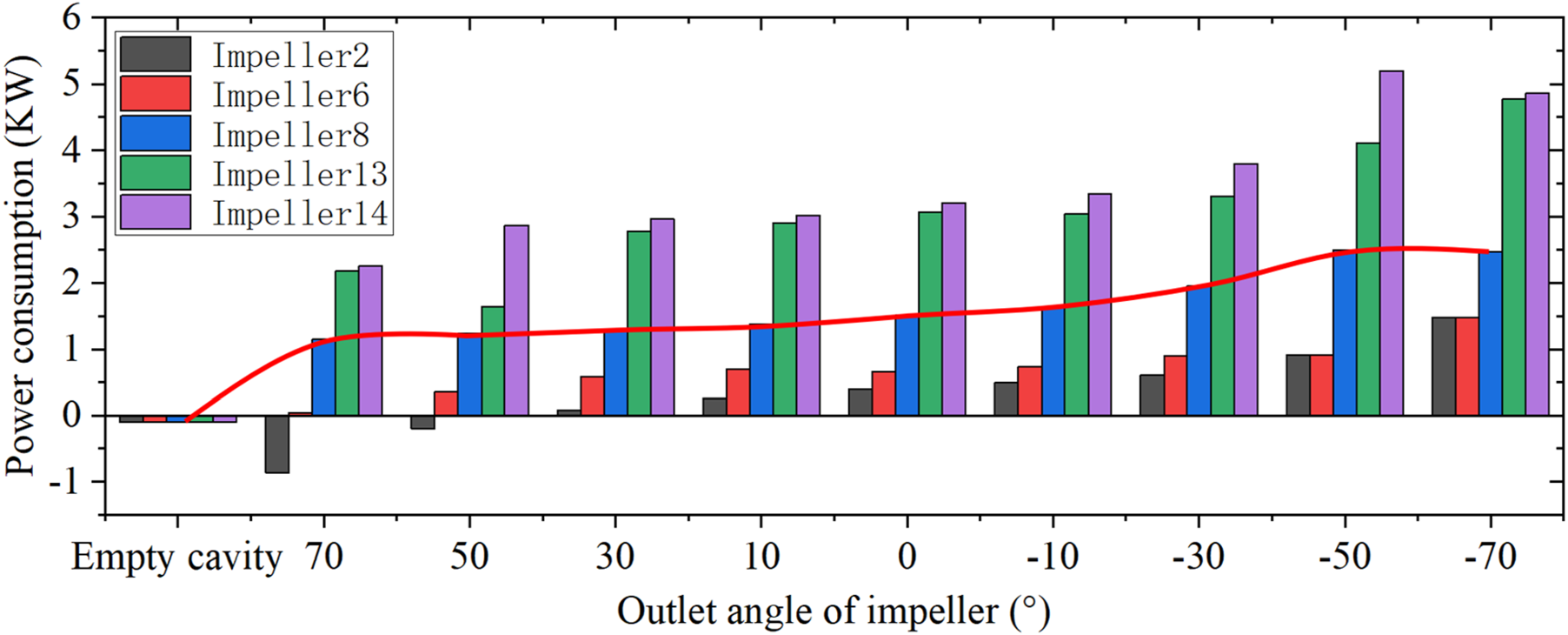
图28(a)显示了不同叶轮出口角度下静压的差异，主要集中于叶轮腔体和系统出口区域。根据公式(1)，叶轮功与腔体出口处的绝对周向速度和局部腔体旋转速度呈正相关，而对数压比与腔体出口处的绝对速度呈负相关。如图25所示，出口安装半径较小且叶轮出口角度较大的叶轮腔可显著降低绝对速度和绝对周向速度，这可能导致静压随叶轮功下降，同时静压随速度。相比之下，对于高安装半径和低叶轮出口角度的叶轮结构，静压因高叶轮功而增加，但因高绝对速度而降低，如图28(b)和(c)所示。从图28(d)可以看出，由于不同结构下变化较小且趋势相似，耗散对静温的影响可以忽略不计。在系统出口处，在总温和焓保持恒定的情况下，静压随绝对速度的降低而升高。此外，随着叶轮出口角度的减小和出口安装半径的增大，静压的区域增量得到增强。

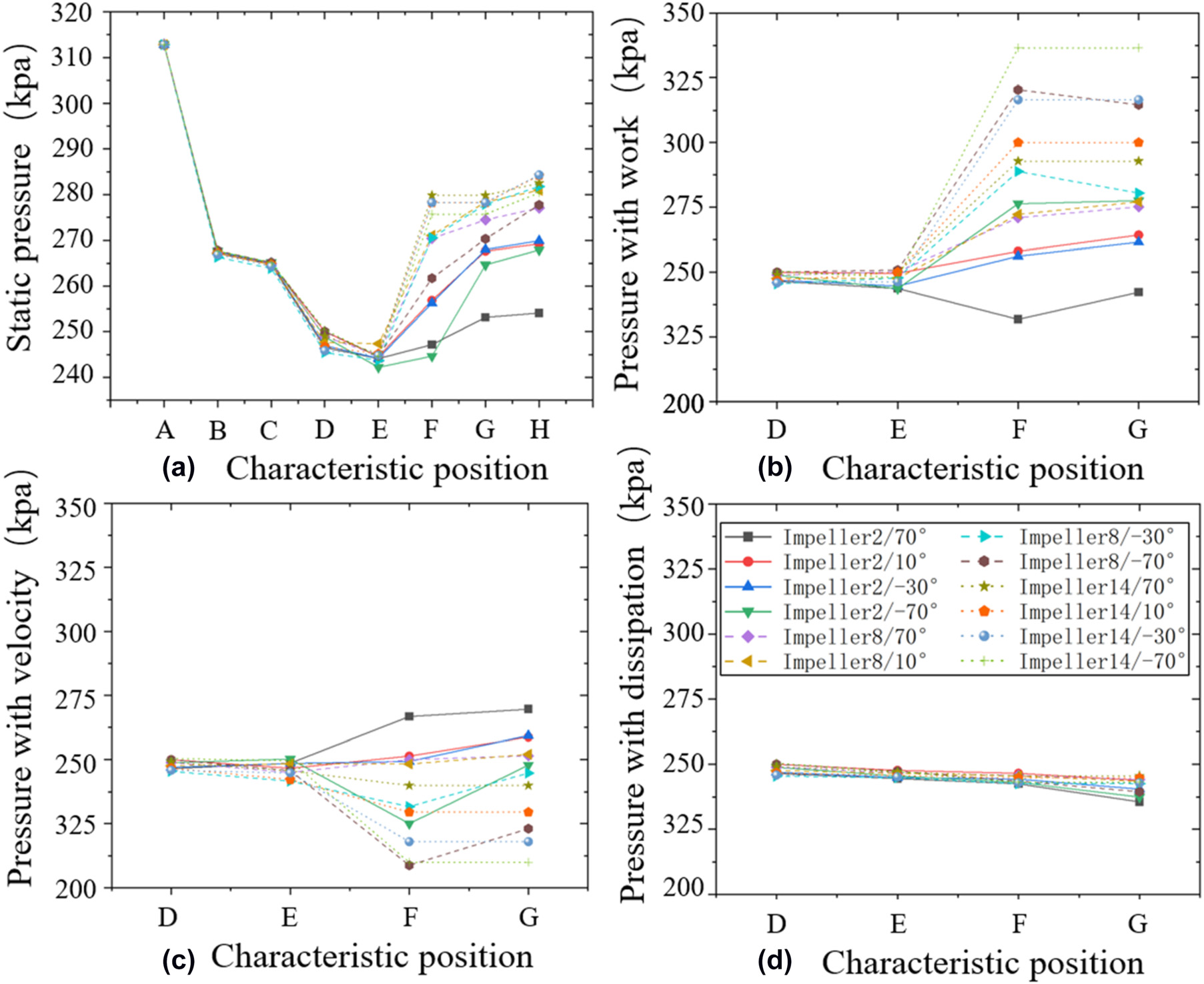静压、(b) 静压与叶轮功关系、(c) 含速度的静压、(d) 考虑耗散的静压随不同叶轮出口角度的变化曲线)

当叶轮结构具有较低的径向安装和较高的出口角时，随着叶轮出口角度的减小，叶轮工作压力的增加是大于速度压力的降低，从而导致静压和系统压力比的增加。当叶轮结构具有较高的径向无论是高径向安装还是低出口角，叶轮功引起的压力下降都可以通过速度得到补偿。此外，与高径向安装和低出口角引起的静压大幅增加相比，不同叶轮出口角度下的压力变化差异可以忽略不计，这意味着相同径向安装、不同出口角度的系统压力比几乎相同，例如图29中叶轮八和叶轮13的情况。

图29展示了叶轮在不同出口角度下的系统压力比对比。在低径向安装和高叶轮出口角度的情况下，随着叶轮出口角度的减小，系统压力比增大。然而，在高径向安装和低叶轮出口角度的情况下，系统压力比基本不随叶轮出口角度的变化而变化。

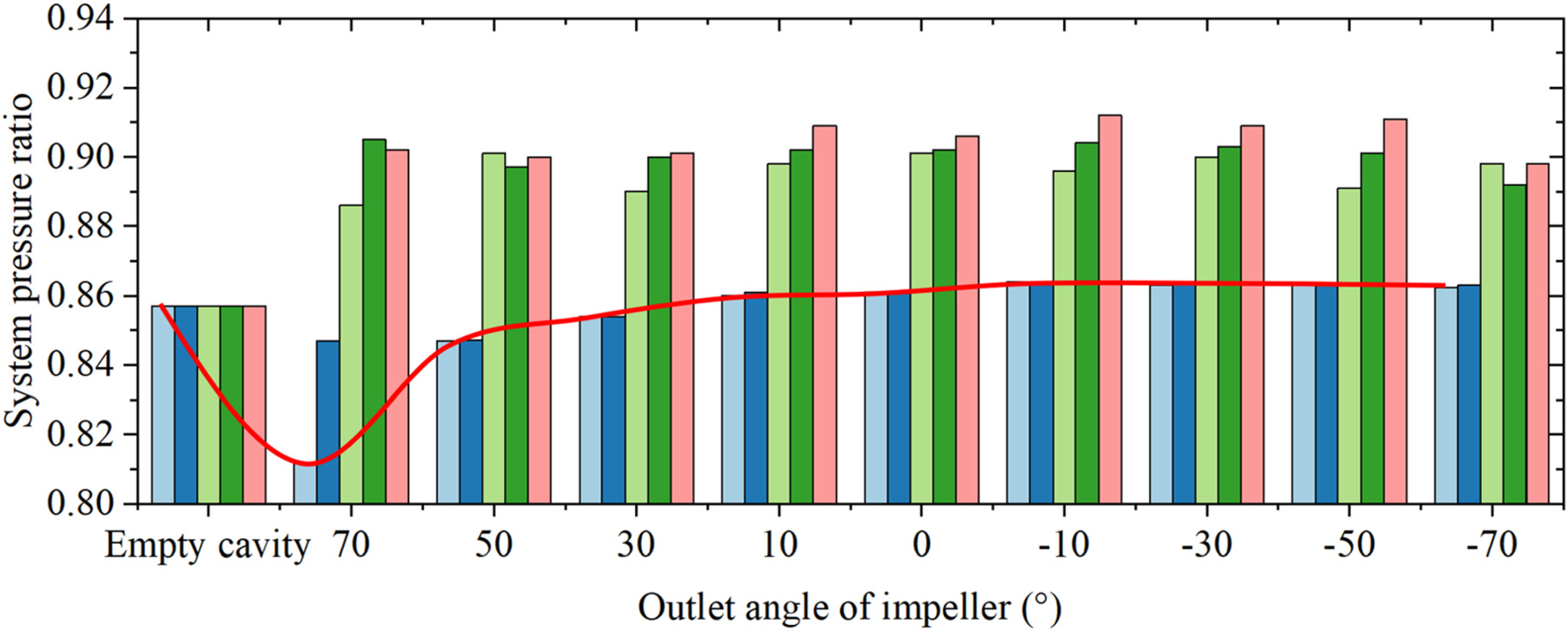
综上所述，叶轮安装位置对压比和功耗的影响最大，而叶轮叶片数对它们的影响最小。在高叶轮安装位置下，出口安装角对压比的影响可以忽略不计。为了减少叶轮数量并降低功耗，叶轮叶片数不应大于24。由于在12–48范围内的特定叶轮叶片数对应的系统压力保持稳定，且功耗随叶轮叶片数的增加而增加，因此叶轮叶片数的选择不宜过高或过低。在较大的叶轮出口安装半径下，不同出口角度对应的压比基本不变，而功耗随着出口角度的减小而增加，因此为实现低功耗，出口角度应选择较高值，例如50°。为了获得高压比和低功耗，叶轮结构应具有高安装半径、特定叶轮叶片数在12–24范围内以及高出口角，如50°。与空腔预旋系统相比，压比最高提升6.4%，功耗最高增加2620 W。

5 结论

本研究采用理论分析和详细的数值模拟方法，对叶轮腔预旋系统的流动特性进行了研究。探讨了叶轮结构对系统性能的影响，提出了一种新颖的理论分析方法和高效叶轮结构。本工作的结论如下：

• 系统功耗主要受接收孔和叶轮腔内功率交换的影响，接收孔内的功耗不受叶轮结构变化的影响。系统功耗随出口安装半径和叶轮叶片数的增加而增加，随叶轮出口角度的减小而增加。
• 系统压力比的变化由叶轮腔和系统出口处的绝对速度及叶轮功决定。出口安装半径越高，叶轮功和绝对速度越高，压力比也越高。在高安装半径下，叶轮叶片数和出口角对系统压力比的影响可忽略不计。
• 为了获得高压比和低功耗，叶轮应具有高安装半径、叶轮叶片数在12–24范围内的特定结构以及高出口角，例如50°。与空腔预旋系统相比，压力比最高提升6.4%，在工况a下对应的功耗增加为2620 W。