本文来自“生信算法”公众号。
对于以Illumina为代表的二代测序技术，研究者们开发出了许多优秀的序列比对算法，如BLAST、Bowtie2 、BLAT等软件。随着测序技术的不断发展，尤其是近几年以单分子测序技术为代表的三代测序技术的出现，测得的序列长度长达十万碱基数，远远高于二代序列长度，且同时具有较高的测序误差（错误率~15%）。因此，绝大多数针对二代测序数据的序列比对工具不适合处理三代测序数据。所以，开发基于三代测序数居的序列比对算法尤为迫切。
在上一篇文章中（三代测序序列比对利器-BLASR，更小更快更方便），算法哥介绍了BLASR三代测序比对算法，BLASR是2012年开发的首个三代序列比对算法，但其运行速度慢。最近又有好多新发表的三代测序比对算法。其中rHAT（rHAT: fast alignment of noisy long reads with regional hashing）作为国内第一篇三代序列比对算法，由哈尔滨工业大学的王亚东教授团队开发，16年发表在Bioinformatics期刊上。博哥作为一个算法开发者，自然需要仔细拜读。因此，本次简单介绍rHAT算法的主要思想，希望对大家有所启发，可以用rHAT来处理自己的序列。
rHAT（Regional Hashing-based Alignment Tool ）算法主要是采用了区域哈希（regional hashing）策略。算法主要分为两部分，首先是定位（在整个基因组中找到与待比对序列相似的区域），通过区域哈希将待比对序列定位到基因组中与其相似的区域，如下图左图所示。然后根据区域内的种子构建有向无环图，找到比对路径进行详细比对，如下图右图所示。
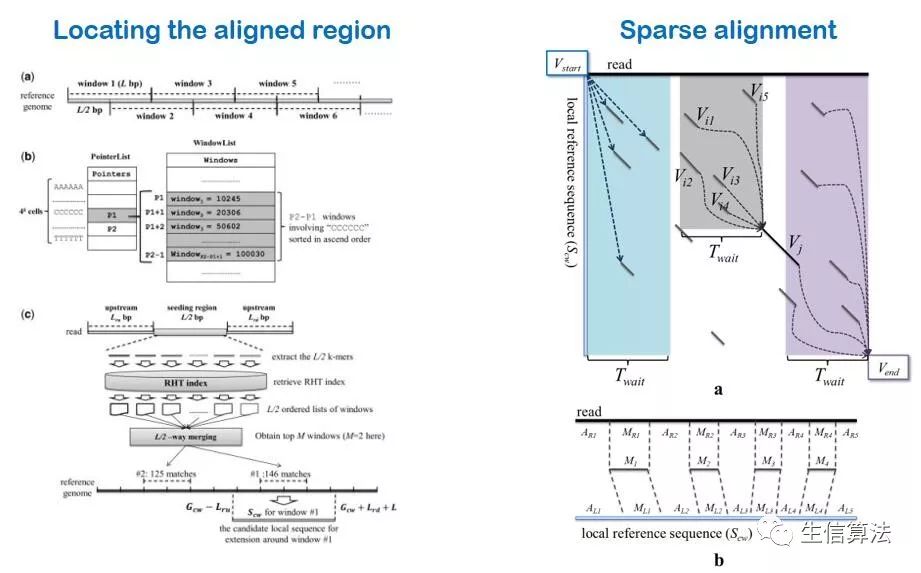
哈希表定位
首先看一下如何通过区域哈希表在基因组序列中对序列进行定位。
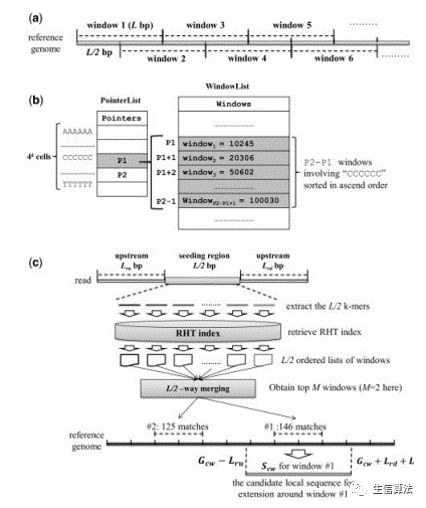
- 如上图a所示，首先将基因组分割成长度为L的窗口，其中相邻两个窗口重叠L/2部分，这就是区域哈希表中区域的意思，一个窗口就是一个区域。
- 然后构建区域哈希表，如图b所示，将基因组每个k-mer（长度为k的子片段，又称作种子）进行哈希编码，每个哈希表中存储的是出现这个k-mer的窗口的位置。
- 然后对于待比较序列，如图c所示，提取待比较序列的每个k-mer，通过图b中的哈希表就可以找到包含每个k-mer的窗口，然后对窗口中的种子个数，即匹配个数，进行排序，找出种子个数最大的窗口，即为与待比较序列相似性较高的区域，用于接下来的序列比对。
序列路径选择与比对
通过上面步骤在基因组中选取待比对区域后，利用种子扩展策略对非种子区域进行比对。
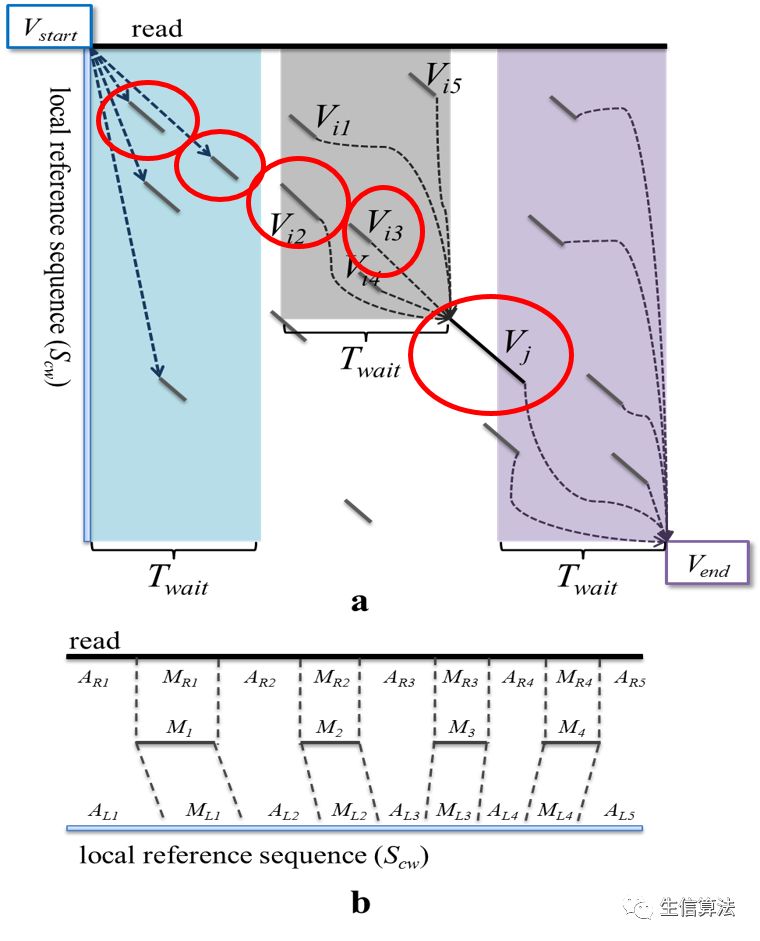
- 首先根据种子构建有向无环图，通过打分策略选取比对路径，如上图中a的红色圆圈所示。
- 找出比对路径中的种子，对种子间的间隙采用经典的动态规划算法进行详细比对
- 最后将种子间的比对结果与种子拼接，合并得到最终的长序列比对结果。
结果比较
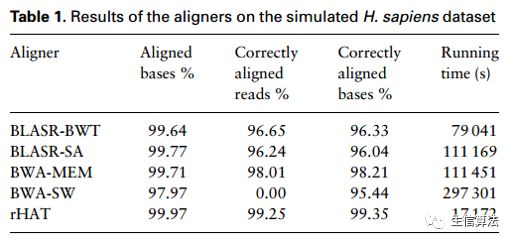
rHAT算法与目前BLASR和BWA-MEM两种方法进行了比较，测试数据为人类基因组数据，如下图所示，可以看出rHAT方法在比对碱基数、比对序列条数以及运行时间均有改善。希望可以对序列分析者有所帮助。详细的比对结果大家可以参考其原文。
代码下载地址：
https://github.com/HIT-Bioinformatics/rHAT
原文链接：
https://academic.oup.com/bioinformatics/article/32/11/1625/1742681
参考文献：
Bo Liu, Dengfeng Guan, Mingxiang Teng, Yadong Wang; rHAT: fast alignment of noisy long reads with regional hashing, Bioinformatics, Volume 32, Issue 11, 1 June 2016, Pages 1625–1631
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
