Threejs/WebGL中旋转变换的原理

已于 2024-03-09 19:18:37 修改
阅读量1k 收藏 12
点赞数 23
CC 4.0 BY-SA版权
分类专栏： WebGL进阶 文章标签： webgl
于 2024-03-09 19:09:48 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/dabaooooq/article/details/136588376
本文介绍了向量的旋转变换，特别是如何在三维空间中使用正交矩阵，如绕Z轴、X轴和Y轴的旋转矩阵，这些在WebGL中用于保持几何形状的长度和角度不变。正交变换具有重要的线性性质和直观的右手法则应用。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

目录

目录

向量的旋转变换 

正交变换 

WebGL中的旋转矩阵

绕Z轴的旋转矩阵

绕X轴的旋转矩阵

绕Y轴的旋转矩阵

向量的旋转变换 

向量p按逆时针旋转α度，可如下表示

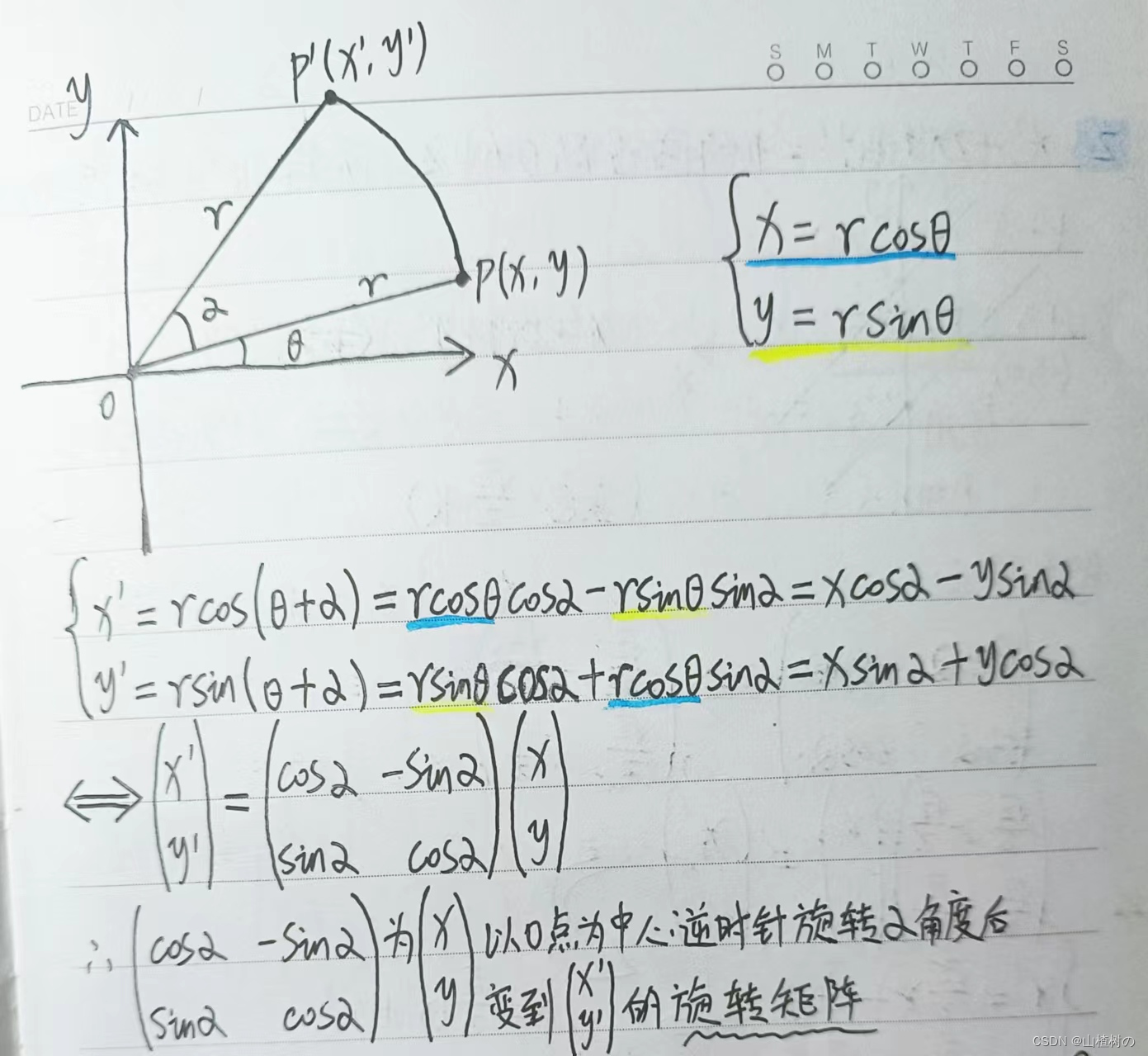
正交变换 

上述旋转变换在高维空间中的属于正交的线性变换，即 p' = Ap，旋转矩阵A满足正交性，称为正交矩阵，正交阵遵循两个条件：

  1. A为方阵
  2. 列（行）向量两两正交且为单位向量

比如：

        每个列向量是单位化：cos^2α + sin^2α 开根号 = 1  

        两两向量的内积为0：(cosα*-sinα + sinα+cosα) = 0

正交变换不会改变向量的内积、长度、夹角，如下图

可知，三维世界中通过正交变换并不会改变几何图形的整体形状，只是相对的改变其位置 

最低0.47元/天 解锁文章

200万优质内容无限畅学
小程序3D效果实现：WebGL与Three.js应用
移动开发前沿的博客
06-11 1065
随着小程序生态的爆发（2023年微信小程序月活已超12亿），用户对交互体验的要求从“能用”升级为“惊艳”。3D效果作为提升用户沉浸感的利器，逐渐成为电商、教育、文旅等领域的“标配”。本文将聚焦如何在小程序中高效实现3D效果，覆盖从底层图形技术（WebGL）到上层开发框架（Three.js）的完整链路，以及具体的代码实战。本文将按照“从抽象到具体”的逻辑展开：假设你是一个“数字画家”，想在手机上画出会动的3D城堡。如果直接用最原始的工具（比如“魔法画笔”WebGL），你需要：这显然太麻烦了！于是有个聪明的发明
three.js实现3D模型任意方向旋转
qq_38229938的博客
07-07 1978
因为业务需要，我们在公司官网使用Three.js实现了可鼠标拖动任意旋转的3D旋转模型，可是实现之后发现除了Z轴方向都可以任意旋转，但是Z轴方向最多只能旋转180度。找遍全网也没有找到相关的资料来解释错在了哪一步，最终还是在github仓库中找到使用案例才得以解决。
矩阵旋转
kingov
09-09 1078
矩阵的概念threejs中的矩阵矩阵的应用用于旋转一个几何体创建一个立方体cube放到场景中；绕向量(1,1,0)旋转30度var axis = new THREE.Vector3(1,1,0); //创建一个三维向量 var rotWorldMatrix = new THREE.Matrix4(); //创建一个4*4矩阵 rotWorldMatrix.makeRotationAx
WebGL长方体动态变换项目：旋转与缩放
最新发布
weixin_42590539的博客
06-07 1092
WebGL（Web Graphics Library）是一种JavaScript API，它提供了一个用于在任何兼容的Web浏览器中无需插件就可以进行3D和2D图形渲染的标准方式。它将OpenGL ES 2.0的标准应用到了网页中，使得开发者能够在网页上绘制出复杂的图形。在现实世界中，要观察一个物体，需要一个相机或眼睛作为观察的起点。在WebGL中，虚拟相机用于定义观察世界的方式，它包含位置、朝向和视野范围等属性。虚拟相机的重要性在于，它决定了用户的观察视角，影响了3D场景的视觉效果和用户的交互体验。
WebGL笔记：图形旋转的原理和实现
Wang的专栏
11-29 460
我们将顶点着色器里的正弦值和余弦值暴露给js，便可以用js旋转图形了。radians(float degree) 将角度转弧度。sin(float angle) 正弦。cos(float angle) 余弦。在js 中修改uniform 变量。// 修改uniform 变量。可以直接在着色器里写旋转公式。// 获取Uniform变量。
three js模型旋转
liuxi_happy的博客
07-12 1145
如何让立方体模型旋转到指定的面。
Three.js使用rotation旋转模型
wz122330的博客
09-02 1万+
Three.js使用rotation旋转模型
WebGL-Threejs:WebGL 和 Three.js 演示
06-23
在"WebGL-Threejs-master"这个压缩包中，可能包含了以下几个方面的内容： 1. **基础示例**：可能有简单的3D物体创建和渲染，例如创建一个基本的立方体或球体，并应用不同的材质和光照效果，展示如何设置相机视角。 ...
HTML5+Three.js WebGL实现超逼真的海中三维水母动画效果源码.zip
11-03
4. **动画系统**：在Three.js中，通过修改物体的属性（如位置、旋转和缩放）来实现动画。水母的摆动和浮动效果可能通过时间线和动画函数来控制。 5. **光照和阴影**：为了增强真实感，项目可能会涉及到不同类型的...
tngt-threejs:Tungsteno中使用的Three.js脚本
05-27
Tngt-threejs项目就是这样一个实例，它展示了如何将Three.js有效地融入到网站开发中，为用户提供动态的三维体验。 一、Three.js基础 Three.js的核心概念包括场景(Scene)、相机(Camera)和渲染器(Renderer)。场景是...
Threejs 模型自身中心旋转
muitoprazer的博客
11-04 1154
模型自身旋转
three.js实现围绕某物体旋转
11-30
话不多说，请看代码： 可以拖动右上角观察变化 <!DOCTYPE html> <html lang="en" style="width: 100%; height:100%;"> <head> <meta charset="UTF-8"> <title>Document</title> [removed][removed] <script src="http://cooklife.cn/html/node_modules/dat.gui/build/dat.gui.min.js
基于Threejs可着色和旋转的3D模型动画特效
12-12
这是一款基于Threejs可着色和旋转的3D模型动画特效。该特效中，通过鼠标的拖动和滚动，可以旋转和缩放3D模型。最大的特点是你可以对模型的各个部分进行自定义着色。
ThreeJs开发（移动，旋转，相机，纹理，鼠标事件等源代码）
11-16
threejs开发小实例，实现了创建场景灯光，摄像机，对物体的移动，旋转，以及摄像机的移动旋转，动画效果，灯光设置（源代码）
WebGL实现两个模型的独立运动：旋转、前进后退、缩放
11-18
WebGL实现两个三维模型的独立运动，包括每个模型的转向、前进后退、缩放功能。此处方向均以运动模型作为参考，模型正面方向为前进，相反方向为后退，绕动物中轴线转向。
Three.js模型对象旋转、平移、缩放变换
u014291990的博客
12-01 7053
Three.js模型对象旋转、平移、缩放变换 本文是Three.js电子书的4.2节 点模型Points、线模型Line、网格网格模型Mesh等模型对象的基类都是Object3D，如果想对这些模型进行旋转、缩放、平移等操作，如何实现，可以查询Threejs文档Object3D对相关属性和方法的介绍。 Object3D方法属性沿X轴平移.translateX ( distance )沿Y轴平移.tr...
【three.js】Camera相机四大参数详解
qq_38196449的博客
03-03 1307
第三个参数和第四个参数就是近端面和远端面，比如我们分别设置是1和3000，相机的位置是(-1000,0,0)，那么近端面的位置就是(-999,0,0)，远端面的位置就是(2000,0,0)。，在两个面之间，我们能看到网格模型，如果网格模型在两个面外，那么你是看不到的。第二个参数我们不多介绍，就是长宽比，一般长宽就是你画布的长宽。先说一个概念，threejs中的相机其实就是一个。我们设置的是30度，当我们调大或者调小来看看效果。near — 摄像机视锥体近端面。far — 摄像机视锥体远端面。
Three.js 旋转 rotation\rotateOnAxis\rotateX
热门推荐
这是个问题
05-12 1万+
属性： 属性名 说明 使用方法 .rotation 物体的局部旋转，以弧度来表示 object3D.rotation.x = 10 注意，这里设置的数值是弧度，需要和角度区分开 角度 转 弧度 MathUtils.degToRad(deg) 弧度 转 角度 MathUtils.radToDeg (rad) 方法： rotateOnAxis 在局部空间中绕着该物体的轴来旋转一个物体 方法 传参 使用方法 .rotateOnAxis ( axis : V
ThreeJS-3D教学六-物体位移旋转
weixin_44384273的博客
10-08 3602
position rotate tween
ThreeJS实现精灵模型与Canvas画布结合的WebGL演示
资源摘要信息:"WebGL/...通过这个Demo，开发者可以学习到如何在WebGL环境中使用Three.js库创建交互式的3D精灵效果，并理解Sprite在WebGL/ThreeJS项目中的应用。这样的技能对于创建高质量的Web交互应用或游戏至关重要。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包

打赏作者

山楂树の

你的鼓励将是我创作的最大动力

¥1 ¥2 ¥4 ¥6 ¥10 ¥20
扫码支付：¥1
获取中
扫码支付

您的余额不足，请更换扫码支付或充值

打赏作者

实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值