费舍尔线性分辩分析(Fisher‘s Linear Discriminant Analysis, FLDA)

费舍尔线性分辩分析(Fisher’s Linear Discriminant Analysis, FLDA)

1. 问题描述

为解决两个或多个类别的分类问题，大多数机器学习（ML）算法的工作方式相同。

通常，它们采用某种形式的转换来对输入数据进行处理，以降低原始输入维度到一个新的（更小）维度。其目的是将数据投影到新的空间中。然后，在投影后，它们尝试通过找到线性分离来对数据点进行分类。例如，我们有如下数据，

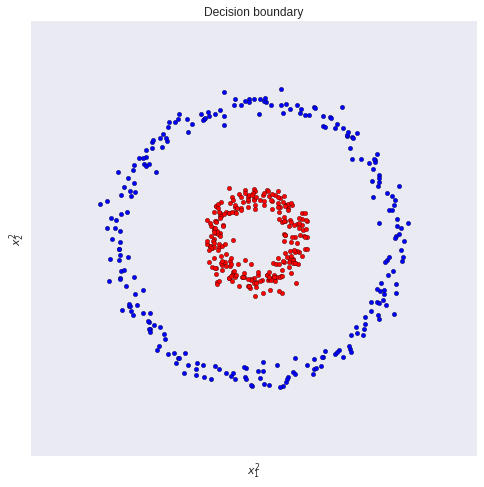
对数据直接进行线性分类显然不是最佳的方法，但是如果我们将数据投影到一维空间，我们可以找到一个线性分类器，将数据分为两个类别。这就是费舍尔线性判别分析（FLDA）的基本思想。我们将数据做如下操作：

$$y=x_0^2+x_1^2$$

其中，$x_0$和$x_1$是原始数据的两个特征。我们可以看到，通过这种方式，我们将数据投影到了一维空间，然后我们可以找到一个线性分类器，将数据分为两个类别。投影后的数据如下图所示：

通常，我们要探寻一种将数据从高维向低维度转换的方式，这被称为表征学习（Representation Learning）。深度学习也是表征学习的 一种，但在深度学习中，我们不需要猜测哪种转换会导致数据的最佳表示，算法会自行解决。

但是，请记住，无论是表示学习还是手工特征，模式都是相同的。我们需要以某种方式改变数据，使其更加适用于分类任务。

2. 二分类情况

假设我们有$C_1$，$C_2$两个类别的样本，每个样本维度为$D$，样本数为$n_1$和$n_2$。我们的目标是找到一个投影矩阵$W$，将数据投影到一维空间：

$$\hat{x}=W^{\top }x$$

设新样本$\hat{x}$的维度为1，则$W$的维度为$D\times 1$。

那么，我们该如何寻找$W$呢？换句话说，我们寻找的$W$应该符合什么条件呢？

这就是费舍尔线性判别（Fisher’s Linear Discriminant, FLD）发挥作用的地方。

费舍尔提出的想法是最大化一个函数，该函数将在投影后的类均值之间产生大的分离，同时在每个类内部给出小的方差，从而最小化类之间的重叠。

换句话说，FLD选择最大化类别间分离的投影方法。为此，它最大化类别间方差与类别内方差之比。

简而言之，为了将数据投影到更小的维度并避免类别重叠，FLD保持了两个属性：

• 数据集类别间具有很大的方差。

• 数据集每个类别内部具有较小的方差。

请注意，较大的类别间方差意味着投影后的类别平均值应该尽可能远离彼此。相反，较小的类别内方差会使投影后的数据点更加接近。

计算每个类别的均值，我们可以得到：

$${\mu }_1=\frac{1}{n_1}\sum _{x\in C_1}x,{\mu }_2=\frac{1}{n_2}\sum _{x\in C_2}x$$

其中，$m_1$和$m_2$分别是$C_1$和$C_2$类的均值。经过投影后，

$${\hat{\mu }}_1=W^{\top }{\mu }_1,{\hat{\mu }}_2=W^{\top }{\mu }_2$$

其中，${\hat{\mu }}_1$和$\hat{\mu }$