1 线性判别分析介绍
1.1 什么是线性判别分析
线性判别分析(Linear Discriminant Analysis,简称LDA)是一种经典的监督学习算法,也称"Fisher 判别分析"。LDA在模式识别领域(比如人脸识别,舰艇识别等图形图像识别领域)中有非常广泛的应用。
LDA的核心思想是给定训练样本集,设法将样例投影到一条直线上。使得同类样例的投影点尽可能接近、异类样例的投影点尽可能远;在对新样本进行分类时,将其投影到该直线上,再根据投影点的位置来确定新样本的类别。
与自然语言处理领域中的LDA不同,在自然语言处理领域,LDA是隐含狄利克雷分布(Latent DIrichlet Allocation,简称LDA),它是一种处理文档的主题模型,我们本文讨论的是线性判别分析,因此后面所说的LDA均为线性判别分析。
1.2 为什么要学习LDA算法
PCA是一种无监督的数据降维方法,LDA是一种有监督的数据降维方法。在训练样本上,即使对数据提供了类别标签,在使用PCA模型的时候不会使用类别标签,而LDA在进行数据降维的时候是利用类别标签的。
从几何的角度来看,PCA和LDA都是将数据投影到新的相互正交的坐标轴上。只不过在投影的过程中他们使用的约束是不同的,也可以说目标是不同的。PCA是将数据投影到方差最大的几个相互正交的方向上,以期待保留最多的样本信息。样本的方差越大表示样本的多样性越好,在训练模型的时候,我们当然希望数据的差别越大越好。否则即使样本很多但是他们彼此相似或者相同,提供的样本信息将相同,相当于只有很少的样本提供信息是有用的。样本信息不足将导致模型性能不够理想。这就是PCA降维的目的:将数据投影到方差最大的几个相互正交的方向上。这种约束有时候很有用,比如在下面这个例子:
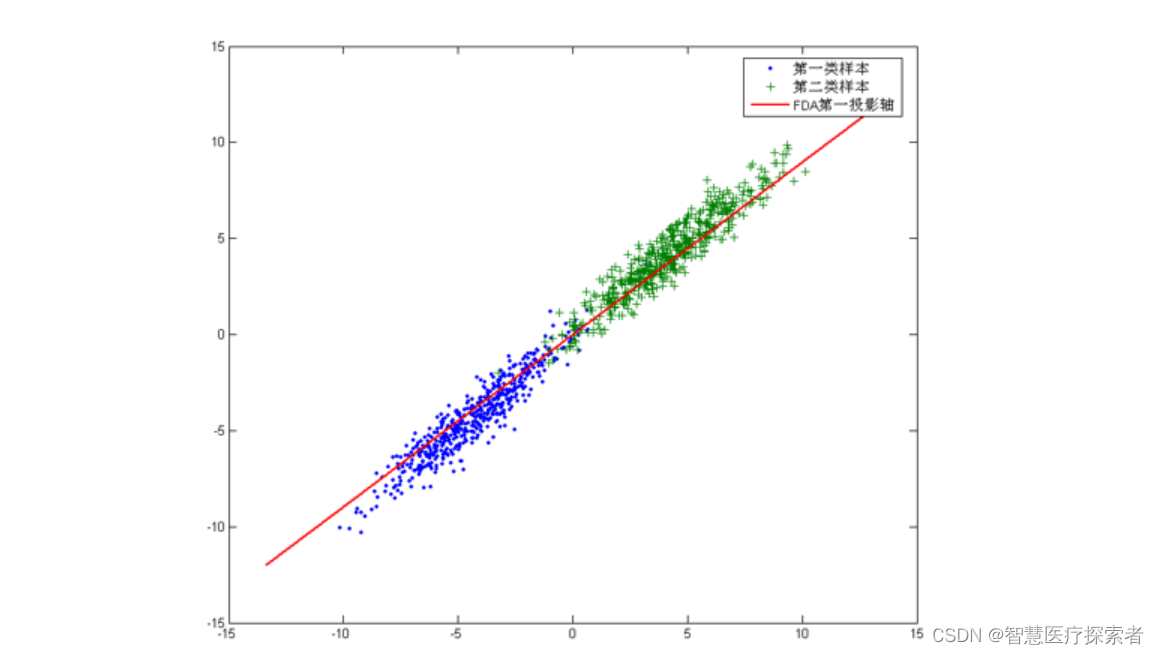
对于这个样本集我们可以将数据投影到 x 轴或者 y 轴,但这都不是最佳的投影方向,因为这两个方向都不能最好的反映数据的分布。很明显还存在最佳的方向可以描述数据的分布趋势,那就是图中红色直线所在的方向。也是数据样本作投影,方差最大的方向。向这个方向做投影,投影后数据的方差最大,数据保留的信息最多。
但是,对于另外的一些不同分布的数据集,PCA的这个投影后方差最大的目标就不太适合了。比如对于下面图片中的数据集:
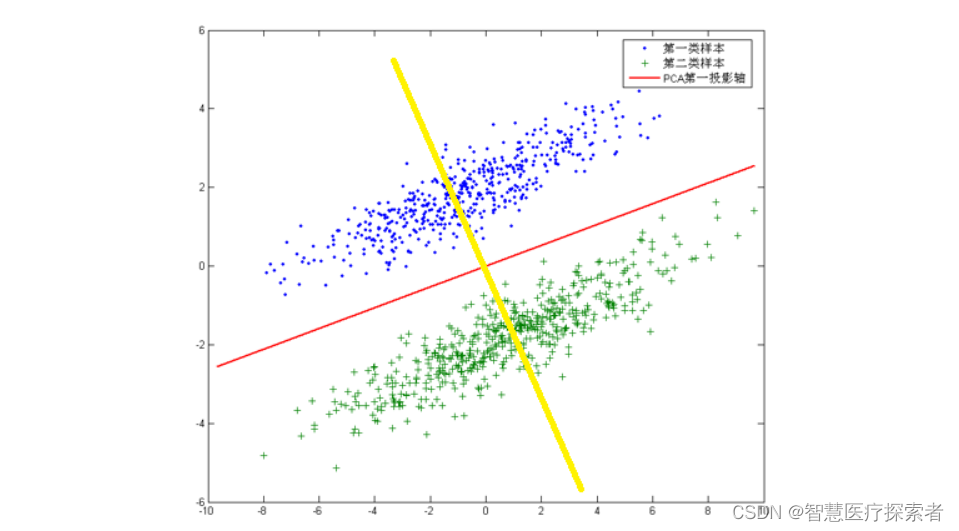
针对这个数据集,如果同样选择使用PCA,选择方差最大的方向作为投影方向,来对数据进行降维。那么PCA选出的最佳投影方向,将是图中红色直线所示的方向。这样做投影确实方差最大,但是是不是有其他问题。聪明的你发现了,这样做投影之后两类数据样本将混合在一起,将不再线性可分,甚至是不可分的。这对我们来说简直是地狱,本来线性可分的样本被我们亲手变得不再可分。而我们发现,如果使用图中黄色直线,向这条直线做投影即能使数据降维,同时还能保证两类数据仍然是线性可分的。上面的这个数据集如果使用LDA降维,找出的投影方向就是黄色直线所在的方向。
这其实就是LDA的思想,或者说LDA降维的目标:将带有标签的数据降维,投影到低维空间同时满足三个条件:
- 尽可能多的保留数据样本的信息(即选择最大的特征是对应的特征向量所代表的方向)。
- 寻找使样本尽可能好分的最佳投影方向。
- 投影后使得同类样本尽可能近,不同类样本尽可能远。
1.3 LDA的思想
LDA的核心思想:类内小,类间大
- 线性分类
指存在一个线性方程可以把待分类数据分开,或者说用一个超平面能将正负样本区分开,表达式为y=wx,这里先说一下超平面,对于二维的情况,可以理解为一条直线,如一次函数。它的分类算法是基于一个线性的预测函数,决策的边界是平的,比如直线和平面。一般的方法有感知器,最小二乘法。
-
非线性分类
指不存在一个线性分类方程把数据分开,它的分类界面没有限制,可以是一个曲面,或者是多个超平面的组合。
LDA是一种监督学习的降维技术,也就是说它的数据集的每个样本是有类别输出的。这点和PCA不同,PCA是不考虑样本类别输出的无监督降维技术。LDA的思想可以用一句话概述,就是“投影后类内方差最小,类间方差最大”,什么意思呢?我们要将数据在低维度上进行投影,投影后希望每一种类别数据的投影点尽可能的接近,而不同类别的数据的类别中心之间的距离尽可能的大。
假设我们有两类数据分别是红色和蓝色,如下图所示,这些数据特征是二维的,我们希望将这些数据投影到一维的一条直线,让每一种类别数据的投影点尽可能的接近,而红色和蓝色数据中心之间的距离尽可能的大。

上图中提供了两种投影方式,从直观上看出,右边要比左边图的投影效果好,因为右边图的红色数据进而蓝色数据各个较为集中,且类别之间的距离明显,左边的则在边界处数据混杂。以上就是LDA的主要思想。在实际应用中,我们的数据是多个类别的,原始数据一般也是超过二维的,投影后的也一般不是直线,而是一个低维的超平面。
周志华老师的《机器学习》中简述了线性判别分析的中心思想,可以联想到方差分析中的组内偏差SSE和组间偏差SSA(Fisher线性判别分析和方差分析的发明者都是R.A.Fisher)。
Fisher判别分析的思想非常朴素:给定训练样本例集,设法将样例投影到一条直线上,使得同类样例的投影点尽可能接近,不同类样例的投影点尽可能远离。在对新样本进行分类时,将其投影到同样的这条直线上,再根据新样本投影点的位置来确定它的类别。
1.4 LDA算法的优化目标
LDA的原理:投影到维度更低的空间中,使得投影后的点,会形成按类别区分,一簇一簇的情况,相同类别的点,将会在投影后的空间中更接近方法。下图来自周志华《机器学习》,给出了一个二维示意图:
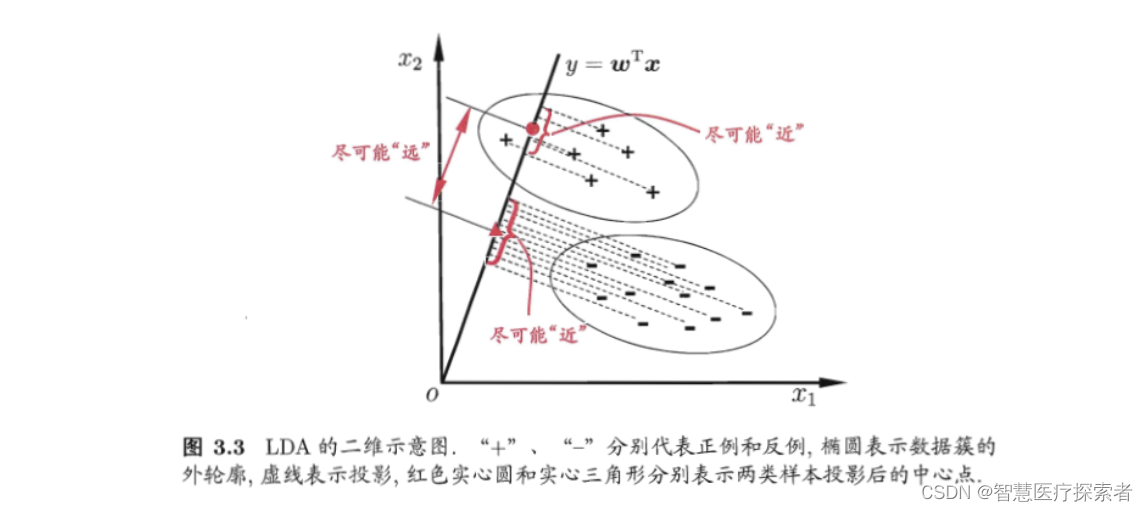
什么是线性判别分析呢?
所谓的线性就是,我们要将数据点投影到直线上(可能是多条直线),直线的函数解析式又称为线性函数,通常直线的表达式为:
![]()
其实这里的 x 就是样本向量(列向量),如果投影到一条直线上 w 就是一个特征向量(列向量形式)或者多个特征向量构成的矩阵。至于 w 为什么是特征向量,后面我们就能推导出来。 y 为投影后的样本点(列向量)。我们首先使用两类样本来说明,然后再推广到多类问题。
将数据投影到直线 w 上,则两类样本的中心在直线上的投影分别为 ,
,若将所有的样本点都投影到直线上,则两类样本的协方差分别为
和
。
投影后同类样本协方差矩阵的求法:
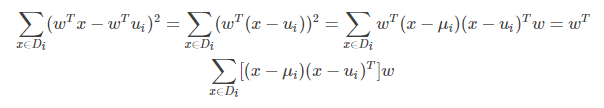
上式的中间部分(即第二行的式子)就是同类样本投影前的协方差矩阵。还可以看出同类样本投影前后协方差矩阵之间的关系。如果投影前的协方差矩阵为 则投影后的为
。
上式的推导需要用到如下公式,a,b都是列向量:
![]()
欲使同类样例的投影点尽可能接近,可以让同类样本点的协方差矩阵尽可能小,即下面式子尽可能小:
![]()
欲使异类样例的投影点尽可能远离,可以让类中心之间的距离尽可能大,即下面式子尽可能大:
![]()
同时考虑二者,则可得到最大化的目标
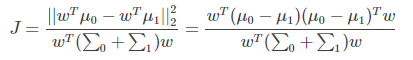
上式 ||*|| 表示欧几里得范数,其中:





 线性判别分析(LDA)是一种监督学习算法,用于分类和降维,尤其在模式识别中广泛应用。LDA的核心是找到投影方向,使得同类样本点接近,异类样本点远离。与PCA相比,LDA利用类别标签信息,目标是最大化类间距离和最小化类内距离。LDA在处理高维数据时,选择投影方向使类间散度矩阵与类内散度矩阵的比值最大,通过特征值分解来实现。在多类问题中,LDA最多降至k-1维。LDA的优点包括降维效果好、考虑类别差异,缺点则包括对高斯分布假设的依赖和对异常值的敏感性。常见应用场景包括模式识别、文本分类和生物信息学等领域。
线性判别分析(LDA)是一种监督学习算法,用于分类和降维,尤其在模式识别中广泛应用。LDA的核心是找到投影方向,使得同类样本点接近,异类样本点远离。与PCA相比,LDA利用类别标签信息,目标是最大化类间距离和最小化类内距离。LDA在处理高维数据时,选择投影方向使类间散度矩阵与类内散度矩阵的比值最大,通过特征值分解来实现。在多类问题中,LDA最多降至k-1维。LDA的优点包括降维效果好、考虑类别差异,缺点则包括对高斯分布假设的依赖和对异常值的敏感性。常见应用场景包括模式识别、文本分类和生物信息学等领域。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章


















 9374
9374

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










