基于Petri网的应急交通灯控制

面向事故易发交叉口的应急交通信号灯控制系统设计

摘要

佩特里网（PNs）被广泛用作对离散事件系统进行建模的可视化和数学形式化工具。本文采用确定性和随机佩特里网设计一种针对事故情况的交叉口紧急交通灯控制系统，以提供应急响应。根据动态PN模型所描述的阻塞交叉路段，设计相应的紧急交通灯策略，以确保交叉口的安全性。文中阐述了受影响交叉口及道路上交通信号灯/设施之间的协作机制。对于上游相邻交叉口，设计了一种基于交通信号的应急控制策略，以防止事故引发的大规模拥堵。同时提出了死锁恢复、活锁预防和冲突解决策略。我们采用可达性分析方法对所构建的模型进行验证。据我们所知，这是首篇应用佩特里网对面临事故的交叉口实时交通应急系统进行建模与设计的研究。该研究可用于提升现有实时交通事故管理和交叉口交通安全的技术水平。

Index Terms— 离散事件系统，Petri网，智能交通系统，交通灯控制，交叉路口事故，交通拥堵。

一、引言

U RBAN 道路交叉口是道路网络中最容易发生事故的区域之一。对于不同国家和地区，30%至60%的伤害事故以及高达三分之一的死亡人数发生在交叉口[1]。这主要是因为交叉口的事故场景属于最复杂的类型之一，不同类别的道路使用者在有限区域内以交叉路径相互作用。某种程度上，交通事故高发使交叉口成为由初次事故引发的二次事故的热点区域，而二次事故可能造成更严重的损害。此外，受伤人员在不慎移动时可能遭受二次伤害。因此，它具有迫切需要有效实施对发生事故的交叉口（以下简称事故交叉口）的科学管理，以防止二次事故和伤害。

交通事件管理（TIM）通过系统性努力来检测、响应和清除交通事故。其目标是快速恢复交通安全与容量[2]，并带来许多可衡量的益处[3],，例如减少燃油消耗、事故持续时间、二次事故以及交通拥堵。在过去三十年中，智能交通系统（ITS）技术被公认为有价值的工具，并在全球范围内应用于交通事故检测[4]–[6],验证[6],响应[7],和通信[8]。为了缓解引发的拥堵并降低潜在二次事故的可能性，交叉口的事故应尽快清除。然而，在未实施急救前，除非伤者处于立即危险中，否则不应移动事故中的伤者。迄今为止，关于如何保障事故交叉口安全的研究尚不多见。

交通信号已被有效用于管理道路空间使用的冲突需求，通过在不同的时间间隔内为不同组相互兼容的交通流分配通行权来实现。为了提高交通效率，人们已开展了大量工作以制定各种策略，这些策略可分为定时式、交通响应式和预测控制三类。第一种由于易于实施且成本较低，在当前的城市交通系统中被广泛使用。第二种根据环形检测器或摄像头等物理传感器检测到的输入信息来控制交叉口，其典型代表是SCOOT和SCATS。还有一些研究致力于提升道路交通安全。例如，Huang等人采用信号控制策略以保障铁路与道路交叉口的交通安全。Weng等人提出利用时间Petri网（TPNs）对并行铁路平交道口的交通安全控制系统进行建模。Huang等人设计了一种针对应急车辆的交通控制系统，明确描述了交通灯行为，以支持应急车辆顺畅通行。当应急车辆在交叉区域遇到红灯相位时，会出现紧急情况，而通过该系统可避免此类状况，并确保应急车辆享有最高优先级通过交叉口。

减少这些冲突交通流可以大大降低潜在碰撞[1]。因此，在事故交叉口，迫切需要立即停止来自某些方向的交通流，以防止冲突，避免发生二次事故。

受伤人员能够获得足够的时间被安全地转移。正是交通信号操作策略帮助我们完成这项工作。事实上，应根据交叉口事故引起的阻塞位置的不同，采取不同的应急策略。

另一方面，上述断流策略可能会在相邻交叉口被阻塞时引发大规模拥堵。例如，图1(a)展示了一个发生事故的交叉口及其引发的拥堵情况。右侧交叉口发生事故并导致其阻塞。当两个交叉口之间的双车道道路充满车辆时，左侧交叉口的蓝色深阴影区域（在后续讨论中称为关键区域）可能会被相应的交通流阻塞。这些区域的阻塞进一步引发了更严重的拥堵，如黄色浅阴影区域所示。可以在这些与事故交叉口相邻的交叉口采用应急交通灯策略，以阻止交通流向阻塞区域行驶，如图1(b)所示。需要注意的是，如果事故清理所需时间较短，在某些情况下（例如非高峰交通时段），前述区域可能不会被阻塞，因此该策略可能并不需要。

佩特里网（PNs）[16],[17]是一种基础扎实的模型，广泛应用于复杂离散事件动态系统的仿真与分析。它们能够很好地建模系统的重要特性，如同步、并发和协同控制。由于其具备图形化表达和数学严谨性，佩特里网已成为描述和分析城市交通[18]尤其是交通灯控制系统[19]–[22]的有效工具。利斯特和切廷使用佩特里网对信号交叉口的控制进行建模[19],，其中为八相位交通设计了信号控制逻辑，并通过该模型实施交通运行安全规则。黄等[20]–[22]采用定时佩特里网对包含二、六、八相位转换的交通信号切换进行建模。他们的目标是建模交通信号灯的复杂相位转换并分析相关属性。

通过发生图分析其性质。Huang et al.[13]率先将确定性和随机佩特里网（DSPNs）应用于并行铁路平交道口（ LC）控制系统。通过控制交通灯运行相位，提取并避免了关键场景，从而保障铁路与道路交叉口的交通安全。

Petri网还被用于交通系统评估研究[23],[24],集体运动的建模与管理[25],以及集装箱码头作业的仿真[26]。可达性树分析方法[27]和多种仿真工具被用于分析构建的模型。

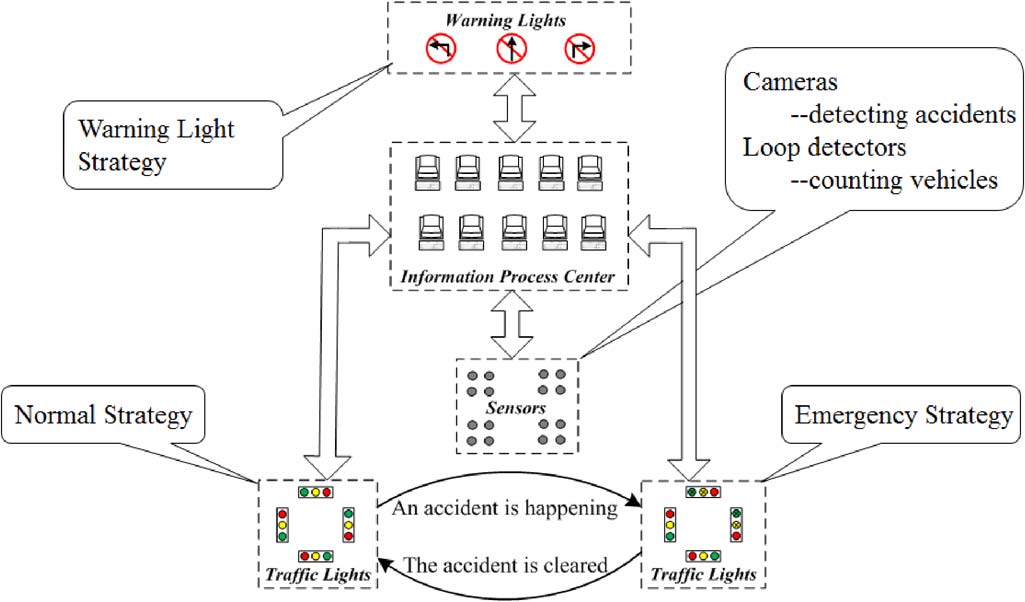
本研究采用DSPN为发生事故的交叉口及其上游相邻交叉口设计交通信号灯控制系统，以防止二次伤害和由事故引发的交通拥堵。可在交叉口安装传感执行器，例如，采用感应线圈通过振动[28]检测车辆移动，而摄像头则用于视觉感知交叉口处的道路交通碰撞[29],[30]。此处，如图1所示，在每个交叉口安装了三种设施：一组交通信号灯、多个传感器和警示灯。所提出的系统的架构如图2所示。传感器用于采集交叉口的实时交通信息：摄像头用于检测事故，环形检测器用于统计车辆数量。警示设施用于向车辆发送事故警告信号。部署了一个信息处理中心（IPC）。通过对传感器获取的实时交通信息进行处理，设计出常规交通信号灯策略和应急策略。此外，这些设施需要适当的协作，这种协作可通过PN模型进行描述。通过这些基于 Petri网的形式化模型，可确保控制系统的正确性，随后可直接通过硬件设计实现该系统。

本文的其余部分组织如下。第二节介绍了信号交叉口、交通网络和交通灯控制。第三节回顾了DSPN，并使用 DSPN构建了正常的交通灯策略及其他设施的运行模式。第四节提出了应急策略，包括针对事故交叉口及其因事故阻塞的关键交叉路段所影响的上游相邻交叉口的紧急交通灯策略，以及应急警示灯策略。同时提出了一些死锁恢复、活锁预防和冲突解决策略。对所构建的Petri网模型的属性分析在第五节中进行了研究。结论在第六节中给出。

第二节. 信号控制交叉口

本节首先介绍一个交通网络，然后设计了一组所使用的交通灯相位转换。我们采用文献[31]–[34]中的思想，将每个交叉口划分为有限个称为交叉路段的部分，并通过相应的交通灯相位来调节交通流对这些交叉路段的占用。我们给出一些将在后续内容中使用的基本符号：R是实数集，R+是正实数集，N={0, 1, 2,…}是自然数集，N+= N/{0}是正整数集，Nk={0, 1, 2,…, k}和N+ k={1, 2,…, k}，其中 k ∈N +。

A.交通网络

本文考虑如图3所示的双向网格网络。在网络中，每个交叉口 Ii, i ∈N +连接八条道路ri,1 − ri,8，分别建模东向、西向、南向和北向方向。道路是车辆从一个交叉口行驶到另一个交叉口所使用的物理区域。如图3所示，交叉口 Ii，其中 i ∈ N + 2连接八条道路 ri,1 − ri,8，其中在ri,1, ri,3, ri,5和ri,7，从 Ii驶出的车辆分别前往西、南、东和北方向；在ri,2, ri,4, ri,6和ri,8，分别从西、南、东和北方向驶来的车辆进入Ii。每条道路 ri,j, j ∈ N + 8 至少包含两条车道，分为两类：r i,j(L)表示 ri,j的最左侧车道，供车辆左转使用，称为左转专用车道（简称为L‐lane）；r i, j(SR)表示另一条车道，供车辆直行或右转使用，称为直行右转车道（简称为SR‐lane）。进入交叉口并左转的车辆从r i,j( L )驶出，而直行或右转的车辆从 r i,j(SR)驶出。注意，r 1,6（ r 1,5）与 r 2,1（ r 2,2）是同一条道路。为方便起见，我们用r i ′ i 表示将车辆从 I ′i 转移到 I i 的道路。 I ′i 称为I i 的上游相邻交叉口。因此，r 1,6（ r 1,5）和 r 2,1（ r 2,2）记为r 21(r12) 。每个交叉口有四个上游相邻交叉口。

B.交通信号灯控制

本文中，在北（n）、东（e）、南（s）和西（w）方向部署了四组交通信号灯。每组有五个信号灯：一个红灯（R）、一个黄灯（Y）、三个绿灯，分别带有直行箭头（GS）、左转箭头（GL）和右转箭头（GR），如图 4所示。车流受图5所示的四相位交通信号灯规则控制，其中四个相位构成一个循环，即从相位 a到 d，然后再回到a。为方便起见，我们用 X n、 Y e、 Z s和 W w分别表示沿 n、 e、 s和 w方向具有特定颜色的交通信号灯，其中 X、 Y、 Z、 W ∈{R, Y, GS, GL, GR}。具体操作如下所述。

1) 相位 a ：南北方向的 GR和 GS信号灯亮起，即GR n 、 GS n 、 GR s 和GSs 开启，东西方向显示红灯信号，即Re 和 R w 开启。直行交通流由北（南）向南（北）行驶表示为 F ns(Fsn),和右边-向西转弯 （东）表示为 Fnw(Fse)。

2) 相位 b ：南北方向亮起 GL信号，即 GLn和 GLs开启，东西向显示红灯信号，即Re和 Rw开启。左转车流从北（南）向转向东（西），记为 Fne（Fsw）。

3) 相位 c ：东向和西向方向的 GR和 GS信号灯亮起，即GRe、 GSe、 GRw和GSw开启，南北向方向显示红灯信号，即Rn和 Rs开启。直行车流从东（相应地，西）向西（相应地，东）行驶，记为 Few(Fwe)，右转车流向北（南）行驶，记为 Fen(Fws)。

4) 相位 d ：东向和西向方向亮起 GL信号，即GLe和 GLw开启，南北向方向显示红灯信号，即 Rn和 Rs开启。左转车流从东（西）到南（北），分别记为 Fes（Fwn）。

C.穿越路段

为了对车辆通过交叉口时的行为进行建模，根据[31]– [34],，我们将每个交叉口划分为有限个物理空间，从而以微观表示的方式高效且清晰地描述交叉口内的车辆行驶路径。交叉口被物理划分的各个部分称为交叉路段。根据我们先前划分的车道，交叉路段可分为三类： L‐路段，即两条 L‐车道的相交部分； LS‐路段，即一条 L‐车道与一条 SR‐车道的相交部分；以及 SR‐路段，即两条 SR‐车道的相交部分。如图3所示，每个交叉口 Ii被划分为16个交叉路段si,j, j ∈N + 16，其中包括 4 L‐路段，即si,6, si,7, si,10和 si,11； 8 LS‐路段，即si,2, si,3, si,5, si,8, si,9, si,12, si, 14和si,15；以及 4 SR‐路段，即si,1, si,4, si,13和si,16。需要注意的是，在前一子章节讨论的四个相位中存在12条车辆移动路径。我们定义交通流 F上的占用路段路径为一系列物理空间的集合，形式化表示为

lF={ri,m→ si,j1 → si,j2 ,…→ si,jk → ri,n|i ∈N +，其中 m, n ∈ N + 8 , ri,m和ri,n是通过交叉口Ii连接的两条车道，si,j 1, si, . . . ,si,j k为 k个交叉路段，即一辆位于 F的车辆可沿一条路径从一条车道ri,m，经过一系列交叉路段，到达另一条车道ri,n。交叉口I i处各交通流的占用路段路径在 图6中清晰地展示，并在下文形式化地给出：

图6 表示了相位 a 中来自 ri,4(SR) 和 ri,8(SR) 并分别直行前往 ri,7(SR) 和 ri,3(SR)，以及分别右转前往 ri,5 和 ri,1 的交通流。 F ns 有一条占用路段路径：l Fns ={ri,8(SR) → si,1→ si,5→ si,9→ si, 13→ ri, 3(SR)}； F sn 有一条路径： l Fns ={ri,4(SR) → si,16→ si,12→ si,8→ si, 4→ ri,7(SR)}； F nw 有两条路径：l Fnw ={ri,8(SR) → si, 1 →r i,1(SR) r i,8(SR) → si,1 → si, 5 → r i,1(L)}；而 F se 有两条路径： l Fse ={ri,4(SR) → si, 16 →r i,5(SR) r i,4(SR) → si,16 → si,12 →ri,5(L)}。请注意，所有交叉口内的直行行驶流均禁止变道移动。此外，在右转行驶流过程中，除非si,16（ respectively，si,1）的前方区域被车辆或其他障碍物阻塞，否则si,12（respectively，si,5）不得占用。

•图6 表示了相位 b中来自ri,4(L) 和 ri,8(L) 并分别左转驶向ri,1 和 ri,5 的交通流，其中 Fsw 有两条路段占用路径：lFsw={ri,4(L) → si,15→ si,10→ si,5→ri,1(L) ri,4(L) → si,15→ si,10→ si, 6→ si,1→ ri,1(SR)}；而 Fne 也有两条路径：lFne={ri,8(L) → si,2→si 11→si 7→ si 12→ ri 5 L ri 8 L → si 2→ si 7→ si 16→ ri 5 SR}, , , ( ) , ( ) , , , , , ( ) 。需要注意的是，来自南的左转车流必须先占用{s},15，然后占用{w},10，而来自北方的车流必须先占用 {e},2，然后占用 {s},7。

类似于 a和 b相位中的交通流， c和 d相位中的交通流也可进行相似分析，但顺序相反。当将交叉口划分为若干交叉路段，并为每种交通流明确定义相应的路段占用路径时，交叉路段阻塞对不同交通灯相位下交通流的影响便变得清晰可见。

III. 常规交通灯策略及其他设施的运行模式

本节回顾了DSPN概念。然后，我们展示了常规交通灯策略、相关传感器操作以及警示灯操作的DSPN构建过程。

A. DSPN模型

一种PN是由三类对象构成的二分有向图。它们是位置、变迁和有向连接位置到变迁以及变迁到位置的弧[17]。确定性和随机延迟可以与Petri网中的变迁相关联，从而形成DSPN [35],[36]。

定义1 ：DSPN 是一个八元组 Σ=(P, T, F, W, H, M0,τ, λ)， 其中

1) P 是一个有限集的位置；2) T= TI ∪ Td ∪ Te 是一个有限集的变迁，划分为三个互不相交的集合 TI、 Td 和 Te，分别表示即时的、确定性的和指数分布的变迁，其中 P ∪ T = ∅ 和 P ∩ T= ∅；3) F ⊆(P × T) ∪(T × P) 是一组有向弧；4) H ⊆ P × T 是从 P 到 T 的一组抑制弧，其中 H ∩ F= ∅；5) W: (P × T) ∪(T × P) → N 是一个权重函数，其中 W(f)>0 若 f ∈ F ∪ H，否则 W(f) = 0；6) M: P→ N 是一个标识函数，其中 ∀p ∈ P， M(p) 表示位置 p 中的令牌数量， M0 表示初始标识；7) τ: Td→R+ 是确定性变迁的触发时间；8) λ: Te→ R+ 是触发速率向量，其元素 λ(t) 是与指数分布时间延迟相关的变迁 t 的触发速率。

在DSPN中，立即变迁在使能后可立即触发；确定性变迁 t具有已知的固定使能持续时间 τ(t)，当 t变为使能时，需等待时长 τ(t)，之后立即触发；随机变迁 t与一个指数分布随机延迟函数相关联，其触发速率为 λ(t)，其使能持续时间服从指数分布。图形上，立即变迁、确定性变迁和随机变迁分别用细条、粗黑条和空心条表示。抑制弧用于表I 图7中变迁与库所的含义及变迁延迟，其中 χ ∈{n, e, s, w}增加模型复杂度。它通过一个小圆圈将位置 p 连接到转移 t， 该小圆圈附着在 t 上。默认情况下，与普通弧一样，抑制弧的权重为 1。因此，只要 p 被标记，它就会阻止 t 触发。抑制弧也可以具有权重 n，在这种情况下，当 p 中至少有 n 个令牌时，它会禁止 t 的触发。为方便起见， G 表示全局时间， G0 表示初始时间。

当构建DSPN模型后，根据其触发规则[35],[36],，可以构造出其可达性图。为了减小图的规模，每条弧对应一个变迁序列，该序列仅包含一个定时变迁（确定性的或随机的）。此外，如果有多个变迁同时触发，则将它们放入括号中，并附加到相应的弧上。

B.交通信号灯控制模型

我们关注的是满足以下条件的交叉口控制策略 [13]：

•交通信号灯顺序形成一个循环；•系统启动时所有交通信号灯均为红灯；•在绿灯转红灯的变迁中采用较短的黄灯持续时间；以及•为确保交通安全，相位转换完成后所有交通信号灯均为红灯。

图7展示了交通信号灯正常策略的DSPN模型，其中规定每个位置的容量为1（即该网是1‐有界的）。位置和变迁及其使能持续时间的含义见表I。为方便起见，令 χ ∈{n, e, s, w}、 ξ ∈{n, s}和 ζ ∈{e, w}。假设初始状态时全局时间为 G 0 = 0，即只有pχ1包含一个令牌，并且t ξ1在 G 0处被使能。它们在5秒后触发，此时 G= 5，令牌分别从pξ1移动到 pξ6和 pξ7，立即使能并触发 t ξ5和 t ξ6，同时 pi2 、pχ1 、 pi6 和 pi7 各获得一个令牌。当 pξ4 和 pξ5触发时， t ξ5 和 t ξ6 获得令牌，从而导致 t ξ7 和 t ξ8 被使能。这表示交通信号灯 GR ξ 和 GS ξ 从全局时间5到25处于开启状态。这意味着灯光从Rξ 变为 GR ξ 和 GS ξ ，且 GR ξ 和GS ξ 的持续时间为20秒。 t ξ7 和 t ξ8 在 τ(tξ7) = τ(tξ8) = 20触发后执行

在 G= 25处持续20秒。然后，一个令牌从 pξ4和pξ5分别移动到 pξ8和 pξ9，从而使能并触发 tξ2，并将一个令牌存放到 pξ3中。这表示交通信号灯 GLξ在全局时间25到35之间开启，即灯光由GLξ变为 Yξ，且 GLξ的持续时间为10秒。接着 tξ3 被触发，导致 pξ2被标记上一个令牌。同时，pi1、 pi4、 pi5和 pi8获得一个令牌。随后，tξ4与 τ(tξ4) = 3以及 tζ1与 τ(tζ1) = 5被使能，并分别在 G= 38和 G= 40处触发。 Yξ的持续时间为3秒。交通信号灯在 Yξ变为 Rξ后切换至 GSζ和 GRζ。与此同时，由于单容量位置 pi2、 pi3、 pi6和 pi7包含令牌， tξ1被禁用。之后，交通信号灯依次切换至GSζ和 GRζ、 GLζ、 Yζ，并在 G= 73时返回其初始状态。在 G= 70被使能的变迁 tξ1在 G= 75处触发，相同的变迁触发序列被重复执行。可达性图如图8所示，其中 M0 − M7均为标记，为方便起见，我们将 M记为灯光状态。因此， M0=(Rn,Re,Rs, Rw)， M1=(GSn,GRn,Re, GSs, GRs, Rw)， M2=(GLn, Re, GLs, Rw)， M3=(Yn, Re, Ys, Rw)， M4=(Rn, Re,Rs, Rw)， M5=(Rn, GSe, GRe, Rs, GSw, GRw)， M6=(Rn,GLe, Rs, GLw)，以及 M7=(Rn, Ye, Rs, Yw)。由于该图是一个包含所有变迁的有限循环，图7中的DSPN模型是活的且可逆的。因此，从标记Mi， i ∈N7开始完成一个循环回到同一标记所需的时间为70，唯独第一次从M0到 M0所需时间为73。注意，交通灯顺序形成一个循环，指导交通灯相位按“ a→ b→ c→ d→ a”循环运行。

C.其他设施的操作模型

我们在交叉口部署包括摄像头和环形检测器在内的传感器，以帮助我们收集交通数据，即事故信息和道路中的车辆数量。通过这些传感器，我们可以制定紧急交通灯策略。具体而言，在每个交叉口 I i处设置一个摄像头，用于获取事故信息，包括事故发生、位置及清除情况[29],[30]。在道路r j 与交叉口 I i的连接处分别安装八个检测器，表示为C i, j, j ∈ N + 8 ，用于统计从r i, j(Ii)驶入 I i(ri, j)的车辆数量。此外，电子显示屏或警示灯是用于向车辆发送事故警告信号的警示设施。此处我们采用警告灯作为警示设施的示例。实际上，在道路 r i ′ i 的中点安装有一组警示灯组。每组包含三个灯，如图9所示，用 w Li ′ ,i , w Si ′ ,i ,和 w Ri ′ ,i ,表示， 用于警示意图进入该路段的车辆

wLi′,i,(b) wSi′,i,和(c) wRi′,i)

基于摄像头 Si 的事故检测DSPN模型，(b) 基于环形检测器 Ci 的车辆计数ADSPN模型, j wLi′,i, w Si′,i , w Ri′,i 其中 j ∈ N + 8 ， 以及 (c) 警示灯的DSPN模型)

表II 图10中位置和变迁的含义，其中 j ∈ N + 8，以及δ ∈{L, S, R}

在下游 Ii分别左转、直行和右转。因此，当下游交通流r i ′ i中断时，信号灯可以警示交通流不要进入下游冲突交叉路段。现在我们为每种设施构建如下基于DSPN的模型。

1) 我们建立了交叉口 I i摄像头事故检测的DSPN模型， 如图10(a)所示（该图中位置和变迁的含义见表II）。t hi 的触发表示事故发生。这是一个低频事件，我们采用指数转移来描述它。 t di 建模了摄像头检测到事故的过程。当 t di 触发时，会在 pai 中填充一个令牌。然后，当清理过程完成时， t ci 触发。

事故清除持续时间由确定性转移的使能持续时间描述，即tci。注意，当tci具有随机时间延迟时， DSPN分析更为复杂。最后，我们假设连续事故之间没有重叠，如位置 pai ′仅包含一个令牌所建模的那样。

2) 环形检测器车辆计数的DSPN模型Ci,j如图10(b)所示。其初始标识为pCi,j_off中存在一个令牌，表示Ci,j未工作。当Ci,j开始工作时，通过将令牌从pCi,j_off移动到 pCi,j_on来触发tCi,j_on。通过触发tCi,j， Ci,j对经过Ci,j的车辆进行计数，这些车辆由pi,j ′中的令牌表示。注意，pi,j ′用作环形检测器与交通流之间的接口。在一个相位周期的工作间隔时间内，Ci,j感知到的车辆总数等于pCi, j中令牌的数量。tCi,j_off的触发表示 Ci,j已关闭。随后 在pCi,j_off中填充一个令牌，并且如果pCi,j包含任何令牌，则使能tCi,j_r。通过反复触发 tCi,j_r， Ci,j被重置， 从而清空车辆数量。

3) 我们构建了如图10(c)所示的警示灯模型，描述了警示灯 wδi ′ ,i, δ ∈{L, S, R}在开启和关闭状态之间切换，分别由pδi ′ ,i_on和 pδi ′ ,i_off ,表示。变迁 t δi ′ ,i_on和t δi ′ ,i_off 是立即的。

图11重点关注由交叉口 I i的交通灯策略控制的环形检测器开关工作。环形检测器受交通灯策略控制，使得在允许车辆通行时，相应方向的传感器开启，而其他方向的传感器则处于休眠状态以节省能量。例如，在模型的初始状态，所有环形检测器均不工作。随后 t ξ1 、 ξ ∈{n, s}触发，t ξ5 和 t ξ6 立即触发，使得GSi 和 GR i 开启，相位 a开始。环形检测器C i,1, C i,4, C i,5以及 C i,8监控相应的道路开启，而其他道路保持关闭。驶出或进入道路 ri,1 − ri,8的车辆数量可分别获得。为了降低模型复杂度并提高其清晰度和可读性，开关工作控制模型将不连接接下来要建模的交通流。因此图10(b)中的pi,j ′在图11中被省略。

D.交通流模型

我们在图12中构建了交通流模型（参见表III中该图各位置和变迁的含义）。此处仅以单条道路 r i ′ i及其下游交叉口I i的交通流为例进行说明，整个网络中的交通流均可通过图12所示模型组合而成。 pi ′ ,μ中的一个令牌表示一辆刚从交叉口I ′i 驶入道路 r i ′ ,μ的车辆。经过一定时间 τ(ti ′ ,i)后，t i ′ ,i 触发，意味着该车辆已通过道路r i ′ ,i ，并准备从r i、v驶入 I i 。注意 r i ′ ,μ ,ri、v和 r i ′ i 是同一条道路。车辆可通过触发t i、vL1、 t i、vS 1或 t i、vR 1实现左转、直行或右转。在pi、v ′生成一个令牌，表示该车辆已从r i、v驶入 I i 。随后通过触发t i、vL1 ′、 t i、vS 1 ′或t i、vR 1 ′，车辆从 I i 驶入道路ri、v1、 ri、v2或 ri、v3，其后续行为依此类推。

表III 图12中位置和变迁的含义，其中δ ∈{L, S, R}、μ, v, v1 − v3 ∈ N + 8

令牌分别注入 pi,v1 和 pi,v1′，或 pi,v2 和 pi,v2′，或 pi,v3 和 pi,v3′。转向率由指数迁移 ti,vL1, ti,vS1 以及 ti,vR1 描述，其触发速率分别为 λi,vL1,λi,vS1 和 λi,vR1。当警示灯亮起时， 即 pδi′,i_ 中存在令牌时，ti,vδ1 不被使能，而 ti,vδ2 被使能， 并以触发速率 λi,vδ2< λi,vδ1 触发。这意味着较少车辆选择警示灯所指示的方向。注意，如果 pi,v′ 中存在令牌，即一辆车辆已从 ri,v 驶入 Ii，则该情况将由 Ci,v 感知，如图 10(b)所示。由于篇幅限制，本文将不再深入讨论交通流模型，而是集中于应急系统的控制逻辑。

面向事故易发交叉口的应急交通信号灯控制系统设计

IV. 应急策略

在本节中，我们针对事故交叉口Ii及其上游相邻交叉口提出紧急交通灯策略，并利用DSPN构建警告灯策略。

A.关键横断面的动态PN模型

首先，我们按如下方式定义交通流运行上的关键交叉路段集。
CSF={Sn|n ∈N +}表示交通流运行
F ∈{Fns, Fsn, Fnw, Fse, Fne,Fsw, Few, Fwe, Fen, Fws, Fes, Fwn}上的关键交叉路段集，其中 Si, i ∈N + n是一个称为关键 交叉路段集的交叉路段集合且
1) 如果存在一个 Si使得 ∀ s ∈ Si被占用，则 F的每条占用 路段路径均被阻塞；
2) 对于每个 Si，不存在 Sj ∈ CSF、 j ∈ N + n 和 j = i，使得
Si ⊂ S j。
我们可以通过以下算法获得CSF。
算法1： 关键横断面计算 一个交通流 F包含 m条路段占用路径，即
l F ={l h |h ∈ 自然数集+ m },
输出: CSF
步骤1：获取每个相关交叉路段的集合
路径在lF中，记为{Sl h|h ∈N + m}，其中如果 l h =
r h → s h1 → s h2 ,…→ s hk → r ′
h , l h ∈ l F , k ∈自然数集 + ,
则 Sl h ={sh1 , s h2 ,…, s hk}；
步骤2： CS F ={Si = ∪ h ∈ N + m
{s ′
h }|i ∈自然数集 + n , s ′
h ∈ Sl h} ;
步骤3：如果 S i ⊆ S j , Si , Sj ∈ CSF ，则从 CS F 中删除 S j 。
根据该算法，我们获得了所有交通流运行的关键交叉路段集 CS。
CS={CSFsn , CS Fse , CS Fns , CS Fnw , CS Fsw , CS Fne ,
CS Few ,CS Fen ,CS Fwe ,CS Fws ,CS Fwn ,CS Fes ,}
其中
CSFsn={{si,4},{si,8},{si,12},{si,16}} CSFse={{si,16}} CSFns={{si,1},{si,5},{si,9},{si,13}} CSFnw={{si,1}} CSFsw={{si,15},{si,10},{si,5, si,6},{si,1, si,5}} CSFne={{si,2},{si,7},{si,11, si,12},{si,12, si,16}} CSFew={{si,1},{si,2},{si,3},{si,4}} CSFen={{si,4}} CSFwe={{si,13},{si,14},{si,15},{si,16}} CSFws={{si,13}} CSFwn={{si,9},{si,6},{si,3, si,7},{si,3, si,4}}
CSFes={{si,8},{si,11},{si,10, si,14},{si,13, si,14}}.
需要注意的是，在本文中，每个交通流运行最多对应 两条路段占用路径。上述关键横断面计算方法对于具有更 多路径的复杂交通流仍然有效。交叉口可以划分为更小的 交叉路段，例如，将一条道路分为三条车道，并将右转专用车道与 SR‐车道区分开来。由此会产生更多的交叉路段， 以及每种交通流对应的更多路段占用路径。
事故的具体位置可以通过摄像头确定和描述。给定由 BS表示的被事故占据的一组交叉路段，可以获得关于关 键交叉路段的以下性质。
性质1：如果 ∃S ∈ CSF满足 S ⊆ BS，则 F被阻塞。
在本文讨论的网络中，我们可以得到以下性质。
性质2：如果 F se（相应地， F en， F nw， F ws）被阻塞，则
F sn（相应地， F ew， F ns， F we）被阻塞。
根据性质1和性质2，我们提出一种算法来描述表示相应
交通流运行的PN模型。令 F BS表示被 BS阻塞的交通流运行 集合。位置pχ,S、 pχ,R、 pχ,L以及pχ,LSR、χ ∈{n, e, s, w}中 的令牌分别表示来自方向 χ的交通流F的直行、右转、左转以 及左‐直‐右运行需要由紧急交通灯策略停止。
算法2： 交通流阻塞模型
输入： BS ⊆{si, j , j ∈ N +
16} 输出：待填入的令牌 pχ, S,
pχ, R, pχ,L，以及 pχ,L SR,χ ∈{n, e, s, w}。步骤1：根据
性质1计算阻塞的 FBS ⊆{Fns , F sn , F nw , F se ,F ne , F sw , F ew , F we , F en ,F ws , F es , F wn} ；

步骤2：如果 Fsn（分别地， Few、 Fns和 Fwe） ∈ FBS，则在 ps、S（分别地，pe、S、 pn、S和pw、S）中填入一个令牌；步 骤3：如果Fse（分别地， Fen、 Fnw和Fws） ∈ FBS，则在ps、 R和ps、S（分别地，pe、R和pe、S、 pn、R和pn、S，以及pw、 R和pw、S）中填入一个令牌；步骤4：如果 Fsw（分别地， Fes、 Fne和 Fwn） ∈ FBS，则在ps、L（分别地，pe、L、 pn、L和pw、 L）中填入一个令牌；步骤5：如果Fse、 Fsn和 Fsw（分别地， Fen、 Few和 Fes、Fnw、 Fns和 Fne，以及 Fws、 Fwe和 Fwn） ∈ FBS，则在ps、LSR（分别地，pe、LSR、 pn、LSR和pw、 LSR）中填入一个令牌。
注意，pχ,S, pχ,R, pχ,L以及pχ,LSR中的令牌由 tdi生 成，当事故清除后，这些令牌由tci移除。还需注意，根据 事故的位置和范围，可能有多条路径被阻塞，因此图13中 的多个位置可能获得令牌。此处我们采用算法2来决定应 添加的弧，以连接pχ,S,{v25},R, pχ,L以及pχ,LSR与变迁 tdi和 tci。若需在p ∈{pχ,S,pχ,R,pχ,L,pχ,LSR}中存放令 牌，则绘制两条弧(tdi,p)和(tci,p)。因此，如图13所示， 构建了关键横断面的动态PN模型。
我们设计了事故交叉口的紧急交通灯策略，使得相应 被阻断方向的交通信号灯应保持红灯，直到事故清除，而 其他方向的信号灯则处于正常运行状态。

B.事故交叉口的紧急交通灯策略

紧急交通灯策略基于图14中的PN模型设计，其中
χ ∈{n, e, s, w}, pα , pβ ∈{pi1 −pi8} 以及由 f1 =(pa , t χ1) 表示
的双面虚线箭头代表一个箭头，满足：若该箭头从 t χ1 到 pα （分别地，从 pα 到 t χ1 ），则箭头 f2 =(pa ,tχ,L SR)从t χ,L SR 到 pα （分别地，从 pα 到t χ,L SR）。与pβ 相关的箭头方向具 有类似性质。我们用χ¯表示 χ的相反方向，即如果 χ是方向 n（分别地， e， s和 w），则 χ¯代表其相反方向。

s（分别对应 w、n和 e）。现在我们讨论如下四种不同的紧 急交通灯策略： 1) 如果位置 pχ,S 存在令牌，则应禁止来自 χ 方向的直 行交通流。该交通流由交通灯 GSχ 控制，此时应关闭。
此应急策略有两个条件：
如果 pχ4 包含一个令牌，则 tχ,S2 被使能并立即触发，通过 从 pχ4 移除令牌并在 pχ8 中生成一个令牌。因此， GSχ 被关 闭。
如果 pχ4不包含令牌，由于从pχ,S到 tχ5的抑制弧， tχ5被阻止触发。如果 pχ6包含一个令牌，则tχ,S1被 使能并立即触发，通过从 pχ6移除令牌并在pχ8中存 入一个令牌。因此， GSχ保持关闭状态。
请注意， tχ2用于灯光GSχ和 GRχ的同步。在应急策 略中，令牌会停留在pχ8，直到 GRχ完成其时间持续时间。
2) 如果 pχ,R 和 pχ,S 中存在令牌，则来自方向 χ 的右 转和直行交通流将被停止。它们由应关闭的 GSχ 和 GRχ 控制。该应急策略有两个条件： 如果 pχ4和 pχ5都包含一个令牌，则 tχ,S2和tχ,R2均被使 能，并通过从它们中移除令牌并分别向pχ8和pχ,R1填入 一个令牌而立即触发。因此，GSχ和 GRχ被关闭。
如果 pχ4和 pχ5不包含令牌，由于从pχ,S到 tχ5的抑制 弧以及从pχ,R到 tχ6的抑制弧， tχ5和 tχ6未被使能。
当 pχ6和 pχ7都获得一个令牌时， t χ,S1和 t χ,R1被使能
并触发，分别向pχ8和pχ,R1放入一个令牌。因此， GS χ
和 GR χ保持关闭状态。
如果pχ,R1包含一个令牌，为了继续交通灯系统
的相位转换，需要通过触发t χ,R 3在 pχ9中填入一个令
牌，这将立即导致交通灯的下一个状态GLχ，即 pχ3
在t χ2 触发后获得一个令牌。但此时 GS χ¯ 和GRχ¯ 被打 开，导致来自 χ的左转交通与来自 χ¯的直行和右转交 通之间发生冲突。为了解决该问题，我们添加了两条
弧(p χ¯9 ,tχ, R 3)和(tχ, R 3,p χ¯9) 。为了使t χ, R 3的触发先于
t χ¯2 ，增加了一条抑制弧(pχ, R 1, t χ¯2) 。
3) 如果位置 pχ,L 存在一个令牌，则来自方向 χ 的左转 车流将被停止。因此，交通信号灯 GLχ 应该关闭。该 应急策略有两个条件：
•如果 pχ3包含一个令牌，则tχ,L2被使能并通过从pχ3移
除一个令牌并在 pχ2中放置一个令牌来触发。因此 GLχ
被关闭。在这种情况下，tχ2和 tχ3均不触发。在图11 中，pCi,y_on_off和pCi,z_on_off无法获得令牌，其中如果 χ ∈{n, e, s, w}, y ∈{7, 5, 3, 1}以及 z ∈{8, 6, 4, 2}，分 别如此。当tχ,L1触发时，相应的环形检测器应被关闭，
因此我们添加两条弧f′ 1=(tχ,L1,pCi,z_on_off)和 f′ 2=(tχ,L1,
pCi,z_on_off)。•如果pχ3不包含令牌，则由于从pχ,L到 它的抑制弧， tχ2未被使能。当 pχ8和pχ9都获得一个令 牌时，tχ,L1被使能并触发，并在pχ2中放置一个令牌。
因此 GLχ保持关闭状态。在这种情况下，tχ3不触发。
当tχ,L2触发时，应通过添加一条弧f′ 3=(tχ,L2,pCi, z_on_off)来关闭相应的环形检测器。
在图7所示的交通信号灯控制系统的运行过程中， 在交通信号灯转换循环期间，一个令牌会被存入或从 pβ方向 χ移除。当GLχ变为 Yχ且 tχ3触发时，一个 令牌会被存入或从pβ移除。然而，在紧急情况下， tχ3不会触发。为了保留 pβ中的令牌，我们添加了双 面虚线箭头f3=(pβ,tχ,L1)和f4=(pβ,tχ,L2)。
4) 如果位置 pχ,LSR 中存在令牌，则禁止来自 χ 方向 的所有交通流。因此，灯 GSχ、 GRχ 和 GLχ 应关 闭。该应急策略有两个条件：
•如果pχ1包含一个令牌，由于从pχ,LSR到 tχ1, tχ1的 抑制弧， tχ1未被使能。在此条件下， tχ,LSR触发，并
向pα和 pβ中的每一个插入或移除一个令牌。注意， pα
和 pβ要么同时具有一个令牌，要么都没有令牌。因此
Rχ保持开启状态。•如果 pχ1不包含令牌，则由于pχ,S, pχ,R和pχ,L中的令牌，所有绿灯都被关闭。如果 pχ2有 一个令牌，tχ4触发并将一个令牌存入pχ1。因此 Rχ被开 启。注意，在此紧急操作中， tχ1和tχ3均不会触发。
双面虚线箭头 f2和f5=(pβ, tχ,LSR)保持了 pα和 pβ中的 令牌。

C.死锁恢复与活锁预防

图14中的紧急交通灯策略模型是否无死锁？本小节回 答了这个问题，并提出了一种控制策略来解决死锁问题。
如果 GL χ , GSχ , GLχ¯ 和 GS χ¯ 需要关闭，则会出现死锁。
在这种情况下，pχ, R 1和p χ¯, R 1均获得一个令牌，并发生循环
等待：t χ, R 3等待 p χ¯9 中的令牌由触发t χ¯, R 3生成，而 t χ¯, R 3等待
pχ9 中的令牌，该令牌由触发t χ, R 3生成。此循环等待导致死 锁。为解决该问题，我们在图15中设计了一个死锁恢复模型。
如果pχ, R 1和p χ¯, R 1都获得了令牌，则 t χχ¯, R触发，在 pχ9 和
p χ¯9 中各生成一个令牌。注意

这会减少控制系统的整个交通灯相位周期持续时间，节省的时 间将用于其他相位。
在所有交通流运行都需要被禁止的特殊情况下， ps1、 pe1、 pn1和 pw1各自包含一个令牌，即信号的状态为 M0=(Rn, Re, Rs, Rw)。在交通控制模型中，将存在一个 触发转移环σ=(tn,LSR,ts,LSR)，(te,LSR,tw,LSR)，使得 M0[σ〉M0。这些变迁无限次地依次触发，从而形成对交 通流无益的活锁。为了防止这种情况，我们设计了如图 16所示的模型。如果所有pχ1、pχ和LSR都包含令牌，则
变迁 tML1触发，在pML中生成一个令牌。由于来自 pML
的抑制弧作用，变迁tn、LSR、 ts、LSR、 te、LSR以及tw、 LSR无法触发，从而防止了 σ的发生。当事故被清除后， pχ、LSR中的令牌被移除，变迁 tML2通过消耗pML中的 令牌而触发，交通灯控制系统恢复到正常运行状态。

D.警告灯策略

本节中，我们利用DSPN提出警告灯策略。设 Ii为事
故交叉口， I′ i 为I i的一个（假设为西侧的）上游相邻交叉
口， I′ i1 −I′ i3 为除 I i外 I′ i 的（北侧、西侧和南侧）上游相
邻交叉口。道路 r i ′ i位于 I i的 χ方向，来自道路
r i1 ′ i ′ − r i3 ′ i ′的交通流分别在 I ′
i 处左转、直行和右转进入道
路 r i ′ i。 r i ′ i处的警示灯策略如图17所示。当pχ,δ中存在令
牌时，通过向 pδi ′ ,i_on 置入一个令牌使警示灯
w δi ′ ,i , δ ∈{L, S, R}开启；当pχ,δ中不存在令牌时，通过将
令牌从 pδi ′ ,i _ on 转移到 pδi ′ ,i _ o ff 使警示灯关闭。
在这种情况下，采用如图18所示的 r i1 ′ i ′ − r i3 ′ i ′,处警
示灯的应急策略，以减少进入r i ′ i 的交通流。在模型中，如 果pχ,δ, t χ,δ触发并在pi,χ存放一个令牌，则描述

该道路在 Ii的 χ方向上的交通流因事故而中断。然后 tLi1′i′_on, tSi2′i′_on,和 tRi3′i′_on被使能，并通过在 pLi1′i′_on,pSi2′i′_on,和 pRi3′i′_on,中放置令牌而触发。因 此，道路上的警示灯wLi1′i′, wSi2′i′,和 wRi3′i′分别点亮。如 果pχ,δ中存在令牌，则判定事故已被清除。ti,χ触发，并从 pi,χ中移除令牌。随后，通过触发 tLi1′i′_off,tSi2′i′_off和
tRi3′i′_off ,，将 pLi1′i′_on, pSi2′i′_on,和 pRi3′i′_on中的令
牌分别转移至pLi1 ′ i ′_off , pSi2 ′ i ′_off ,和 pRi3 ′ i ′_off。因此，
wLi1 ′ i ′, wSi2 ′ i ′,和 wRi3 ′ i ′被关闭。

E.上游相邻交叉口应急策略

本节采用前一节中的假设和符号，为Ii的上游相邻交
叉口（即 I′ i ）设计交通灯应急策略。有两种情况需要采用 应急策略。
1) ri ′ i中的所有交通流在其应急策略作用下于 I i处停止，
即在pχ,LSR中存在一个令牌。2) ri ′ i中的部分交通流在
I i处停止，且通过环形检测器检测到道路 r i ′ i上的车 辆数量达到最大值Ω。
请注意，在情况1中，由于正在执行红灯信号，任何
要进入r i ′ i 的车辆都无法通过I i 。因此，立即采用紧急交通
灯策略，以阻止交通流进入 r i ′ i 的 I ′
i 。在情况2中，如果道
路 r i ′ i 上有足够多的车辆占据，I ′
i 的交叉路段（例如图1中 的蓝色深阴影区域，称为关键区域）可能会

表IV 位置含义
被阻塞。因此，如果 r i ′ i 中的车辆数量达到Ω，也需要采取应急 策略。
现在，我们通过图19至图21中的DSPN提出紧急交通 灯控制策略。其中变迁和位置的含义见表IV和表V，所有 变迁均为瞬时变迁。
如图19所示，如果p χ,L SR 中存在令牌，则t emm1 被使能并触 发。结果，一个令牌被传递
表V 变迁含义
从 pnor 转移到 pemm ，表示正常策略已更改为应急策略。只 有在事故被清除时，该策略才会被暂停，即在 pχ,LSR 中不存在 令牌，使得通过将令牌从 pemm 转移到 pnor 而触发 tnom1。
如果 ri′i 中的部分交通流被停止，而其他交通流被允许 通过 Ii，则在 pχ、L、 pχ、S 或 pχ、R 中至少存在一个令牌， 并且在 pχ、LSR 中没有令牌。此时 pi、χ 接收一个令牌。
pcap_i′i 描述了由安装在 ri′i, 入口和出口处的环形检测器 Ci、
j 和 Ci′,j ′ 分别计数得到的 ri′i 中的车辆数量。从 pcap_i′i 到 temm2 绘制一条权重为 Ω 的有向弧。如果 ri′i 中的车辆 数量达到 Ω，即 Ω 个令牌存在于 pcap_i′i, temm2 中，则使 能并触发，从而将一个令牌从 pnor 转移到 pemm，表示正常 策略已切换为应急策略。当满足以下任一条件时，该策略被 暂停：1）事故已被清除，即在 pχ、L、 pχ、S 和 pχ、R 中均 无令牌，使得 tnom1 触发并将令牌从 pemm 转移到 pnor；2） 道路 ri′i, 中没有车辆，即在 pcap_i′i, 中没有令牌，然后 tnom2 触发，将令牌从 pemm 转移到 pnor。在第二个条件下， 若 ri′i 中的车辆数量再次达到 Ω，则重新执行应急策略。
应急交通灯策略如图20所示。与事故交叉口的控制策略 类似，交通信号灯 GLχ1、 GSχ2和 GRχ3需要保持关闭，而 其他信号灯则按正常运行方式进行控制，其中χ1 − χ3为道路
ri1 ′ i ′ − ri3 ′ i ′的方向。因此，令牌被放置在pχ1,L ′, pχ2,S ′和pχ3, R ′中，如图21所示。
现在，我们给出一种计算Ω的方法。首先，ri ′ i被划分为 两个不同的区域：下游排队存储区（DA）和上游“蓄水池”（UR），如图1所示。当UR充满车辆时，在 I′ i 处采用应急 交通灯控制策略。首先，我们定义以下符号来描述交通状况：
• L RD, LUR, LDA：分别为UR路段、DA路段的道路长
度。• L h：两辆连续排队车辆在同一条车道上的平均车
头时距（前后车辆前端之间的距离）。• L ′
h ：后一辆车 辆从排队状态开始启动时，两辆连续排队车辆之间的最
小平均车头时距。• a：车辆的平均加速度值。
• v：车辆的最大速度。
我们确 实我们的计算基于以下假设 ions:
上述符号的值已知为常数，除了 LUR和 LDA。这两个 交叉口安装有相同的信号相位，如表I所示。通常情况 下，每个循环中在 c和 d相位结束后，DA路段内没有 剩余车辆。
定理1 ：如果DA路段的车辆队列尚未充满到迫使UR中 的车辆停止的程度，则 ri′i所能容纳的最大车辆数如下所示：
Ω= ⎢⎢⎢⎣ 2LRD
v√2(L′ h −Lh)
a+ Lh
⎥⎥⎥⎦ (1)
其中
x 是向下取整函数，表示小于或等于 x ∈ R 的最大整数。
证明 ：在满足I′ i不被阻塞的条件下，ri′i所能容纳的 最大车辆数的计算方法如下：当UR段第一辆车到达DA时， DA段最后一辆车开始移动。根据这些假设，我们可以得 到以下公式：
at2 2= L′ h − Lh (2)
LDA Lh
= Ω 2 (3)
Ωt 2 =
LUR
v (4)
LRD= LDA+ LUR (5)
其中 t表示排队车辆与其后继车辆启动行驶的平均时间间 隔。然后我们可以得到 ri′i所能容纳的最大车辆数为(1)。

V. 属性分析

在本节中，我们讨论所提出的DSPN模型的性质。需要注意 的是，除图10(a)和图12中的DSPN外，所有DSPN均不包含指数 变迁。

A.冲突解决

冲突出现在图18、19和21的DSPN中。在图18和19中， 如果位置pχ、L、 pχ、S以及pχ、R中至少有两个包含令牌，
则变迁t χ、L、 t χ、S以及 t χ、R之间会产生冲突，即只能有一 个令牌被存入pi、χ，且一个变迁的触发会阻止另一个变迁的
触发。为了消除该冲突，我们规定t χ、L、 t χ、S以及 t χ、R的
触发优先级依次降低，例如，若t χ、L和 t χ、S被使能，则由
t χ、L具有最高的触发优先级而触发。实际上，触发序列不 会影响模型的最终状态，即pi、χ将接收到一个令牌。另一个
冲突出现在图18中的t Li1 ′ i ′ _on、 t Si2 ′ i _on和 t Ri3 ′ i ′ _on之间。我 们将其优先级定义为递减顺序。由于这些变迁均为瞬时变迁，
因此pLi1 ′ i ′ _on、p Si2 ′ i ′ _on和p Ri3 ′ i ′ _on将立即接收令牌
表VI 与时间相关的变迁
时间作为结果。类似地，我们给予 tem1 − tem3和tno1 − tno3
优先权以解决相应的冲突。

B.可达性分析

我们通过可达性分析来验证DSPN的性质和正确性。
可达性分析使用可达性图进行，该图可通过手动方式构建。
本文采用一种构建方法：每条弧对应一个变迁序列，且该 序列仅包含一个定时变迁（确定性的或随机的）。此外， 如果有多个变迁同时触发，则将它们放入括号中，并附加 到相应的弧上。显然，这种构建方法可以显著减小图的规 模。可达性分析也可借助诸如TimeNET [37]之类的工具 完成。一些 recently 提出的可达性分析方法可用于分析 大规模和无界Petri网 [27],[38]–[42]。
在本文提出的模型中，与时间相关的转移分为五组， 如表VI所示：A1中的确定性变迁用于建模交通信号的时间 持续时长； A2中的指数转移描述事故的发生；A3中的确 定性转移表示事故的处理过程； A4中的指数变迁刻画车
辆在 Ii处的转向率；A5中的转移表示车辆从 I′ i到 Ii的行 驶时间。我们的目的是验证所设计策略的控制逻辑的有效 性，因此我们并未过多关注交通流模型。指数转移增加了 可达性分析的复杂性。幸运的是，在我们的情况中仅存在 一个指数转移，在构建可达性图时，我们允许它在有限个 时间间隔内发生。此外，无需使用仿真方法即可验证控制 逻辑的有效性。
因此，我们可以构建图11中DSPN模型的可达性图， 以及通过移除图19中与图12的非安全交通流模型相关的
pca p _i ′ i,位置、 t Ci, j _r和 t Ci ′ , j
′ _r变迁及其相关弧后，得到 图10(a)与图13–21中各模型组合后的模型的可达性图。由 于篇幅限制，此处不予展示。对其分析结果表明，这些 DSPN模型是活的且可逆的。

VI. 结论

本工作使用DSPN设计了一个针对事故交叉口的交通 信号灯控制系统。为事故交叉口及其上游相邻交叉口分别 设计了正常和应急交通信号灯策略。应急
提出了警示灯策略。基于Petri网的控制逻辑被证明是有效 的。与[13]和[14],相比，除了考虑不同系统的安全性外， 我们的主要贡献在于：1）我们采用交叉路段的概念构建 了一个基于Petri网的动态模型，用以表示交通流的阻塞情 况；2）我们分别对来自四个方向的交通信号灯进行控制； 3）交通信号灯不仅可以被控制，还能反过来控制其他设 施，包括环形检测器和警示灯。未来工作将构建一个完整 的交通流模型。基于该模型，可以开展一些仿真，以展示 所提出的系统在交通事故管理和交通拥堵预防方面相较于 传统自演化情况的优势。据我们所知，这是首次提出基于 Petri网的针对事故交叉口的应急系统。该系统有望用于提 升城市道路交叉口实时交通事故管理的现有技术水平。