异构机器人协同运输框架

最新推荐文章于 2025-11-13 11:28:01 发布

原创最新推荐文章于 2025-11-13 11:28:01 发布 · 303 阅读

6 ·

CC 4.0 BY-SA版权

文章标签：

#协作运输 #任务分配 #路径规划

使用异构机器人进行协作物体运输

摘要

近年来，多机器人系统已被应用于许多不同的场景中。其中之一是物体运输问题，该问题具有诸多应用，例如简单的物体搬运，以及在更复杂的场景中执行任务，如建筑工地和结构组装中的典型任务。尽管已有大量研究致力于这一看似相对简单的任务，但该问题的多个方面仍然尚未解决，亟需进一步探索。在本研究中，我们提出了一种完整的方法，涵盖该问题的所有相关阶段（i.e.路径规划、任务分配和控制）。通过在模拟机器人和真实地面机器人上进行的多项实验，对该方法进行了全面的评估与验证。

关键词 ：协作运输 · Object操作 · Task分配

1 引言

近年来，移动机器人在许多不同场景和应用中的使用显著增加。这些自主系统在监控、搜索与救援、物体运输等活动中的应用已广为人知。

上述所有活动既可以单独执行，也可以协作执行，在后者情况下称为多机器人系统（MRS）。使用多个机器人具有多种优势，例如增强的鲁棒性，以及在大多数情况下完成任务的时间减少。然而，此类系统的使用也带来了许多挑战，例如机器人定位、路径规划、任务分配和控制。使用此类系统的一个显著优势是能够执行困难的任务而无需专门化的代理，例如使用简单的机器人来运输物体，而不是复杂的机械臂。

使用多机器人系统完成任何任务都涉及许多必须考虑的子问题。在这些问题中，我们可以突出机器人的定位、路径规划、协调和任务分配。定位问题与代理本身以及机器人所处的环境工作以及它们交互的其他任何物体。路径规划问题可以通过多种方式解决，例如在某些情况下，旨在最小化总时间或总体行驶距离。关于团队协调，涉及代理之间的任务分配，以及如何组合可用资源以在遵守所有可能限制的情况下完成活动的研究。

机器人系统应用的主要活动之一是物体的运输与操作。这些任务虽然简单，但在我们日常生活的许多活动中都至关重要，例如运输动作，以及在执行任务时对物体和工具的操作。运输动作大致可分为两类：（i）抓取式操作，即机器人抓握物体；（ii）非抓取式操作，此时机器人通过投掷、滚动或推动等动作来完成运输[5,12,13,16]。

尽管机器人在特定任务上仍不具备人类同等的灵巧性，但机器人可能实现更高的效率和有效性。此外，机器人可以轻松部署到火灾、深海和核事故等恶劣且不宜居的环境中作业。另一个例子是坍塌矿井，这种环境对人类可能完全无法进入，而机器人代理则有望利用其操作臂清理通道，进入隧道和空腔。随着服务机器人不断提升其操作能力，它们在家庭中的应用正稳步增加，目前已有大量研究致力于将机器人用于老年人和患者的家庭辅助[9]。

本文的主要贡献是一个用于异构机器人组通过抓取式和非抓取式操作协同运输一组物体的框架，重点在于任务分配阶段。我们提出了一个完整框架，涵盖了该问题的所有相关阶段。该方法在模拟环境和真实环境中均进行了评估，展示了该技术在满足任务需求（如最小化执行时间或能耗）方面的有效性与灵活性。

本文其余部分组织如下。下一节讨论了文献中关于自主运输问题不同方面的相关工作。第3节介绍了我们的方法，描述了用于规划每个物体路径、分解为段以及机器人选择所使用的机制。第4节展示了在模拟和真实环境中进行的实验。最后，第5节讨论了结果并指出了未来的研究方向。

2 相关工作

使用一组机器人进行物体运输包含许多步骤，例如路径规划、任务分配和团队控制与协调。本研究涉及这三个方面，但主要关注任务分配阶段。

具备操作和运输物体能力的机器人适用性已显著提升，主要旨在提高效率并获得不同方面的收益。

许多研究展示了使用多机器人系统（MRS）模型进行物体运输的实际应用，考虑了抓取式和非抓取式技术。[5]中展示了一种使用地面机器人的协作运输，其中代理包围物体并移动它以避开障碍物。另一个例子是Kiva系统[8]，一种在仓库中用于操作商品的解决方案，主要被亚马逊1等公司使用。使用四旋翼无人机团队，可以基于预先存在的段[11]，或使用积木[2]来构建结构。

使用自主机器人代理进行建造的一个例子是空中机器人建造（ARC），它定义了项目设计和制造范式的转变。在该研究中，揭示了此类系统的特征：（i）支撑结构的建造无需框架即可完成，（ii）数字模型可以很复杂，并且代理明确地由该模型引导，以及（iii）系统在不依赖环境的意义上具有可扩展性[25]。

在许多情况下，集中控制有助于涉及多个代理的问题中的决策和任务分配。[14]的作者提出了一种利用任务实例概念的技术，该概念由单个代理在一段时间内必须执行的工作来表征。在运输中，可以定义包含搜索、清除障碍物和物体移动等动作的任务实例。结合集中控制，使用势场是一种简单且直观的规划方法，可通过添加双极函数[22]，进行优化，或通过回答以下两个问题的控制方式进行分段：(i) 如何在环境中导航；(ii) 如何操纵物体[26]。

另一种协调方式基于领导者‐跟随者方法。一个例子是文献[6]中提出的工作，该工作通过应用任务分配算法MURDOCH[7]来体现这一技术，其中一个代理充当watcher，向负责推动的pusher代理告知应施加于物体的速度，以使其到达目的地。在这种情况下，领导者并不直接参与运输任务。相比之下，另一项研究提出了领导者向团队中的其他机器人通报其轨迹，以便它们在运输过程中跟随的情况[21]。

constrain-move方法由[1]提出，是完全分布式协调的一个示例，其中一组机器人被划分为两个子群：一个子群限制物体的移动，另一个子群驱动运动。这两个团队协同并同时工作，将物体运送到其最终位置。采用相同的运动限制思想，还可利用势场技术，该技术分为三个步骤实施：（i）代理被物体吸引，（ii）然后均匀分布在物体周围，最后（iii）移动到最终位置并携带物体[20]。

任务分配阶段可以描述为一组方法，用于在团队代理之间分配任务，并管理协调方面，直到任务完成。[4]通过将任务分配问题转化为图着色问题来解决此问题，其中每个代理代表一种颜色，每个顶点是需要访问的位置。类似地，[23]展示了一个多智能体控制系统，该系统求解一个二元整数线性规划（BIP）问题并生成分配矩阵。

为了充分探索环境，[17]的作者提出了一种基于拍卖的方法，该方法不仅考虑了代理的出价，还结合路径规划来决定由哪个代理执行任务。

为了使用一组代理来检查船舶，[3]的作者将环境描述为一个图，其中每个节点是一个必须访问的房间，并通过其特征进行描述，例如是否被淹没或存在障碍物。根据可用资源（如代理类型和能力），可以将子团队分配到特定区域，同时提出了一种次优的总行驶距离解决方案。

[24]中展示了两种任务分配方法的对比，其中代理必须运输一批包裹。第一种方法是集中式规划器，它拥有环境各个方面的信息，例如生产频率和分配给每个代理的任务。基于这些信息，集中式规划器决定某个特定代理是否应执行任务或保持待机模式。另一种方法是分布式方法。在这种情况下，每个代理仅拥有其周围环境、源位置和投放位置的信息。为了决定是否从任务执行切换到待机模式，代理根据特定的预定义规则进行决策。

3 方法

使用一组机器人解决物体运输问题可以分解为多个步骤，例如路径规划、任务分配与协调以及团队控制与协调。本文研究了所有这些方面，而本工作的主要贡献在于任务分配与协调阶段。

3.1 问题描述

在已知环境中，我们定义W ⊂ R³为一个凸多边形的工作空间。设R={r₁, r₂,…, rk}由 k个机器人组成，每个机器人的类型定义在 T={中，包括地面车辆和空中类型，其中<地面车辆>类型只能推动物体，而<空中>类型能够抓取并携带物体飞行。我们定义O={o₁, o₂,…, oy} 为需要运输的物体集合。同样地，我们定义集合B={b₁, b₂,…, bx}为不可移动的障碍物集合，这些障碍物将限制机器人和物体的运动。

运输问题被定义为将物体 oi ∈ O从其初始位置 S移动到最终位置Sd，两者均位于W中。来自R的一组机器人将负责移动每个物体，并使总成本最小化运输（时间和能量），并考虑B施加的约束。主要目标是描述一组可由代理执行的计划P，以最终实现所有物体的运输。大多数研究中的规划过程主要关注机器人如何导航，而本文则聚焦于物体轨迹，该轨迹将引导机器人的路径。

该问题从两个子问题入手：（1）物体路径规划——根据效用函数（第3.2节）为物体创建路径，用于指导机器人进行运输；（2）任务分配与协调——根据代理完成任务的表现对其进行评估，并协调其执行任务。

示意图0

图1展示了一个框架的流程图，其中突出了运输过程中的各个步骤：（i）工作区定义，（ii）运输过程中要执行的动作规划，（iii）代理之间的任务分配，（iv）任务的协调与执行。每个阶段将在接下来的小节中进行描述。

3.2 效用函数

在物体和代理的路径规划过程中，为了考虑机器人的异构性，会分析与机器人类型相关的某些特性，以找到最优的类型来满足系统需求。

从这个意义上说，针对每种代理类型评估两个参数，这两个参数描述了在计划P中执行某个动作 ai的有用性，通过效用函数来量化该动作，以便进行比较。评估过程中使用了以下特征：

– 位移时间 ：在W中移动单元之间所需的时间。此方面与机器人执行给定位移的平均速度相关。由函数 Υ(·)描述；
– 位移成本 ：在单元格之间移动的成本。针对运输中使用的每种类型的机器人，计算其在位移过程中的平均能量消耗。由函数 Ψ(·) 描述。

形式上，公式1描述了效用函数 Θ(·)，该函数针对特定类型的机器人进行评估，并根据其特性得出一个评分。该分析生成的值用于指导物体的路径规划过程（如第3.3节所述）。

$$
Θ(t_i, a_i) = α · Υ(t_i) + (1 − α) · Ψ(t_i). \tag{1}
$$

由 α ← {α ∈ R | 0 ≤ α ≤ 1}定义的常数被用作两个考虑方面之间的权重因子，以反映对某些活动的优先级排序，例如以最短时间执行任务或以最低能量消耗执行任务。该模型具有灵活性，因为它可以重新配置以满足不同的需求，并加入每个代理的规划特殊性。该函数的计算结果被用作搜索最优移动方案所使用的启发式方法的一部分。

计划P的总体效用通过计算计划中每个结构 n的效用值之和得到，公式如下：

$$
Θ_p(P) = \sum_{i=1}^{q} Θ(k(n_i)). \tag{2}
$$

考虑到效用函数基于代理的类型ti和某个动作 ai，我们定义了公式3，该公式直接从n中提取此类信息，定义如下：

$$
k: n → t_i, a_i. \tag{3}
$$

Equation2用于确定多个移动计划中哪一个是最优的，换句话说，就是执行动作总成本最低的那个计划。其使用将在第3.3.5节中进一步详细说明。

3.3 路径规划—物体

运输物体的第一步是创建运动计划，该过程分为两个阶段：（i）路径规划和（ii）路径分割。后者将作为机器人路径规划的基准。

所提出的方法是一种基于创建搜索图的经典树搜索算法的变体。首先，我们定义集合F，用于描述搜索扩展期间所有可用的节点，以及集合SN，包含所有已探索的结构 n。

集合F包含在n的扩展阶段创建的状态。选择效用成本最低的结构 n进行扩展。

在执行开始时，一个新节点 n被创建，描述物体的初始位置，并添加到 F中。算法1描述了树节点的扩展过程。

算法1 搜索扩展 (M, F, SN, W)
1: n ← 从(F)中选择状态
2: SN ← SN ∪ {n}
3: S ← 获取位置(n)
4: 对于所有 ai ∈ M执行
5: S′ ← 应用动作(ai, S)
6: Sr ← 是否可执行(ai, S′)
7: 如果 S′ ∈ SN 或是否碰撞(W, S′) 或非 Sr 则
8: SN ← SN ∪ {S′}
9: 继续
10: 结束如果
11: n′ ← 创建节点(S′, Sr, ai)
12: F ← F ∪ {n′}
13: 结束循环

函数 iscolliding 用于验证物体是否与任何 bi ∈ B 发生碰撞，而函数 isexecutable 首先考虑是否存在类型为 t 的可用代理能够执行动作 ai，然后评估该动作是否可执行；若可行，则计算机器人完成该移动所需的位置 Sr，如果该位置通过碰撞检测，则视为有效移动。

搜索算法在两种情况下结束：(i) 当F= ∅时，表示不存在到达目标状态 Sd的路径，或(ii) 当选中的 n处于最终状态的邻域中时，在这种情况下，将创建一个新节点 n并添加到计划中——该节点定义了向状态 Sd的移动。

分割步骤执行由搜索算法创建的计划P的划分，生成集合S作为结果。该集合将在机器人的规划阶段以及后续的任务分配中使用。

为了执行分割，需要创建一个辅助集合Sp，其中包含用作段基础的 n节点结构的引用。算法2描述了该集合的创建过程。

算法2 分段点集创建 (P,Sp)
1: 对于 ni, ni+1 ∈ P执行
2: 如果是空中(ni) 并且是空中(ni+1)那么
3: 继续
4: 结束如果
5: ani i ← 获取动作(ni)
6: ani+1 i ← 获取动作(ni+1)
7: 如果 ani i != ani+1 then
8: spi ← 创建段点(ni, ni+1)
9: Sp ← Sp ∪ {spi}
10: 结束如果
11: 结束循环

使用所有分割点创建一个段集合S，即 spi ∈ Sp。每个段是原始计划P的一个部分，包含一系列节点结构。算法3给出了段的创建步骤。

算法3. 段集创建 (Sp, S)
1: 对所有 spi, spi+1 ∈Sp 执行
2: 如果 S= ∅ 则
3: si ← 创建段(So, sp1i)
4: else
5: 如果是最后一个(Sp, spi)那么
6: si ← 创建段(sp2i, Sd)
7: else
8: si ← 创建段(sp2i, sp1i+1)
9: 结束如果
10: 结束如果
11: S ← S ∪ {si}
12: 结束循环

此过程完成后，集合S被定义为包含 e个段，每个段被分类为具有集合T中的某一运动类型。图2(a) 展示了在特定环境中对一个物体进行规划的示例。

分割在陆地运输中尤为重要。考虑到<地面>机器人只能推动物体，每当需要方向改变时，机器人必须从另一侧推动物体，而此时可能存在另一个代理更具能力的情况以比当前正在执行任务的代理更低的成本完成该操作。

此外，即使方向多次改变，空中运动也可能不需要进行分段。这一限制的原因是，从代理开始空中运动的那一刻起，另一个代理只有在物体被放置后，即空中运输完成后，才能接手移动该物体。

每个段 si，由一系列 n 结构组成，类似于一个计划，因为它也定义了状态 So 和 Sd。这些状态用于机器人路径规划。

3.4 路径规划—代理

在物体移动阶段的路径规划和分段结束后，开始对参与任务的代理进行路径规划阶段。这些计划将在任务分配阶段中使用。

此步骤中使用的路径规划算法类似于算法1（第3.3节），但有以下修改：

– 使用函数进行的碰撞检测是 colliding以机器人本体为参考；
– 函数 is executable未执行，因为它仅适用于物体。

除了每个段的So和 Sd状态外，还创建了一种新的状态类型 I，并将其定义为每个机器人的初始状态。基于这些状态对代理进行路径规划。所生成的计划根据以下两种集合进行分类：T P={初始、过渡、移动}和集合TM={预运输、运输}，如下所述：

– 初始：从状态 I到状态 Sr的计划，该计划描述了段 So的结构。此计划确保代理到达运输将开始的状态。它被分类为类型<预运输>；
– 过渡：从段 si中状态 Sd的位置Sr到段 si+1中 So的位置 Sr的计划。通过此计划，代理可以在另一段中继续运输。它被分类为类型<预运输>；
– 移动：从段中 So的位置Sr到 Sd的位置 Sr的计划。在此计划中，物体在该段内被正确运输。它被分类为类型<运输>。

所有创建的计划都被添加到集合RP={rp₁, rp₂,…, rpⱼ} 中。这些值用于为所有智能体执行任务分配（第3.5节）。

示意图1
示意图2

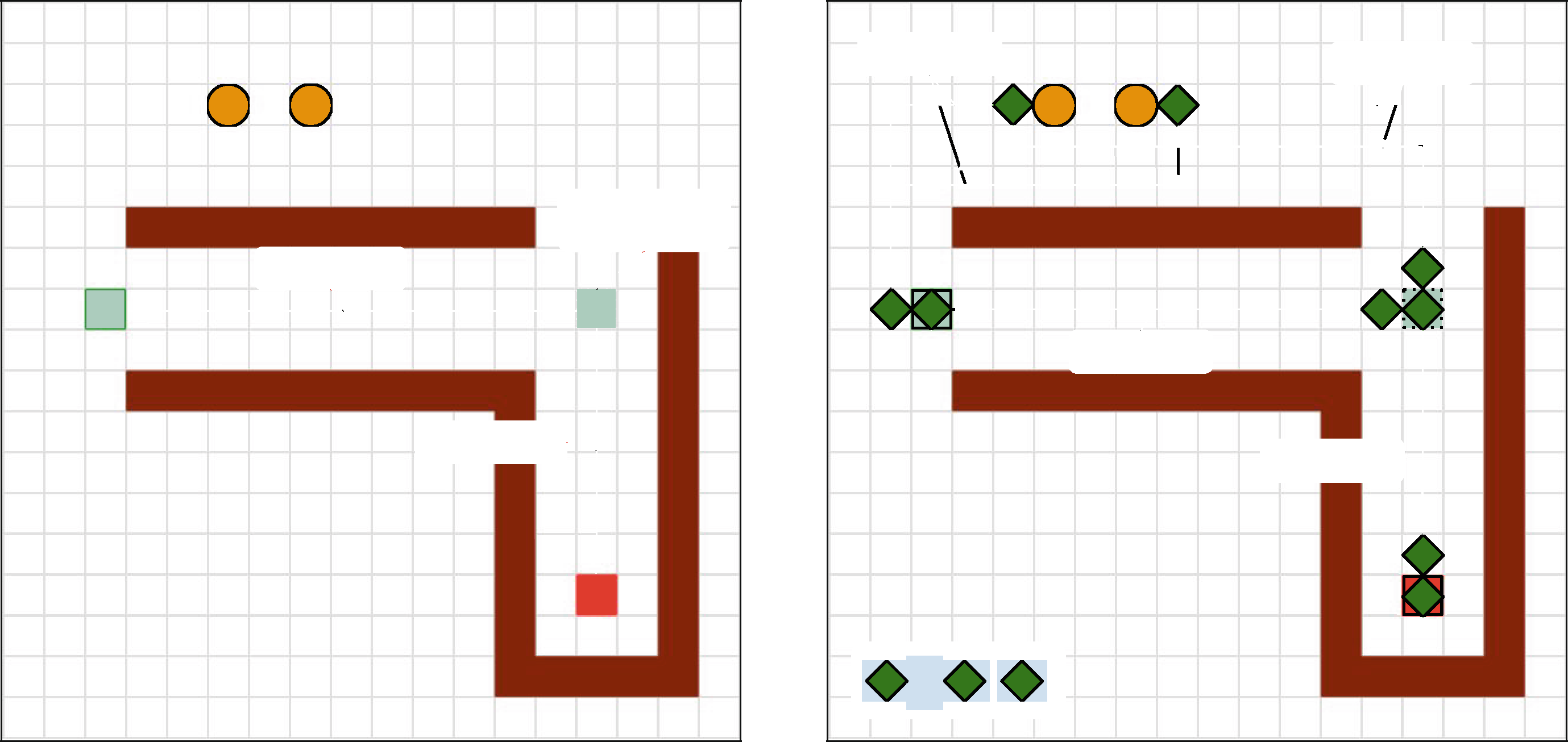
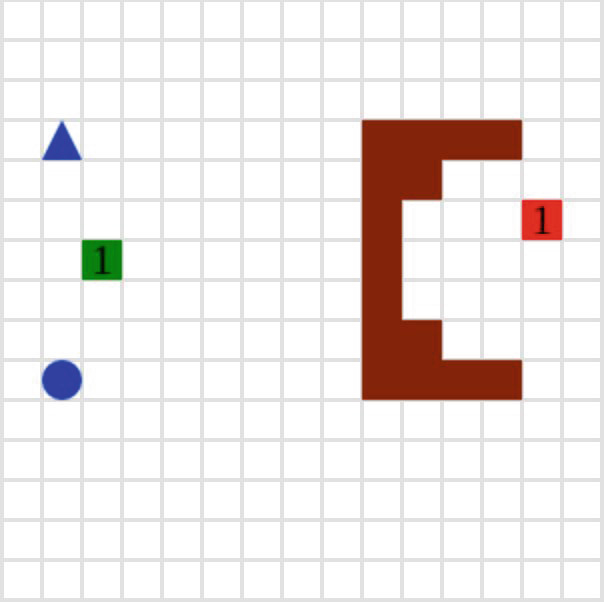
图2. 包含一个物体和两个代理的示例工作空间。（a）显示待执行的物体路径规划，（b）显示代理的规划。

根据集合TM的类型对计划进行分类的原因是，代理要在给定段si上执行物体的运输，必须首先执行预运输类型的移动，然后执行运输类型的移动。

3.5 任务分配

在任务分配步骤中，目标是确定一组移动，这些移动执行后将最终实现物体运输到期望的最终位置，同时最小化总效用函数。

为了执行物体运输，需要创建一个集合EP={ep₁, ep₂,…, eph}，称为执行计划，其中包含来自集合RP的一系列执行计划，这些执行计划被串联起来以实现任务完成。创建集合EP的一种方法由算法4说明。

算法4。执行计划集创建 (S)
1: 对于所有 si ∈ S执行
2: rpi ← 获取计划(si, <预运输>)
3: ri ← 获取机器人(rpi)
4: rpj ← 获取计划(si, <运输>, ri)
5: 执行计划集合 ← 执行计划集合 ∪ {rpi, rpj}
6: 结束循环

在算法4中，函数get plan根据作为参数传入的类型从一个段中检索一个随机计划 rp，或者也可以基于指定的机器人检索计划。函数get robot仅获取负责该计划的代理。为了计算生成的执行计划集合的成本值，将每个计划 epi的成本进行汇总，如下所示：

$$
Θ_t(EP) = \sum_{i=1}^{h} Θ_p(ep_i). \tag{4}
$$

通过执行计划由算法4创建，可以完成物体运输，但目标是获得成本最低的执行计划集合EP，称为 EP∗，形式化描述如下：

$$
\arg \min Θ_t(EP^*) = \min \sum_{i=1}^{h} Θ_p(ep_i). \tag{5}
$$

创建执行计划集合 ∗的过程采用图表示法，并应用最小生成树（MST）算法。用于执行任务分配的图生成方法如算法5所示。通过这些步骤，可以创建图 AG中展示的图

算法5。任务分配图创建（S，R，RP）
1: 对于所有 si ∈ S执行
2: So ← 获取起点(si)
3: Sd ← 获取目标(si)
4: 创建顶点(So, AG)
5: 创建顶点(Sd, AG)
6: 结束循环
7: 对于所有 ri ∈ R执行
8: I ← 获取初始位置(ri)
9: 创建顶点(I, AG)
10: 结束循环
11: 对所有 rpi ∈ RP执行
12: create edge(rpi, AG)
13: 结束循环

示意图3

图3。该图示例了使用 Θp（公式 2）计算出的每条边的成本值。

图生成算法使用了多个函数：get origin获取段的起始节点；gettarget获取段的终止节点；cre-ate vertex在图上创建一个新顶点；get initial position获取代理的初始位置；以及create edge在两个顶点之间创建一条边。

为了以优化的方式执行最小生成树算法，可以对 AG图进行简化，减少所需的边数。这是基于第3.4节中的描述实现的，其中必须按顺序考虑的每一对边被合并为单条边，其权重为原始边权重之和。图4示例展示了相同的图 AG，但以简化形式呈现，称为 AGc。

示意图4

图 AGc与图 AG具有相同的效用值，因此在压缩版本中进行的任何操作都可以映射到原始图上。此外，图 AGc中的边现在有两种类型的 tpi ∈ TP，即实例<初始、移动>和<过渡、移动>。

为了在代理之间选择最优的计划并完成任务分配，从图 AGc出发，应用 Kruskal算法，并遵循以下规则：
1. 边的选择遵循集合S中段的相同顺序；
2. 在一次边选择后，所选机器人类型为<初始，移动>的边将从下一轮选择阶段中移除；
3. 并且，其他机器人类型为<过渡，移动>的所有边也将被移除。

规则1被使用是因为每个物体的运输必须按照先前制定计划中的预定顺序执行；规则2是必要的，因为通过该类型边执行运输的机器人将不再处于其起始位置，无法再执行此类移动。考虑到规则3，没有其他机器人可以执行此类移动，因为只有唯一一个代理能够完成它，即之前已被选中的那个代理。

执行最小生成树算法后，图 AGc将区分出使总效用值最小的边集。图4展示了这一点，其中绿色的边被选中，红色的边被舍弃。

回想一下，图 AGc中的每条边表示图 AG中的两条边，因此边选择可以扩展到完整图。基于此，选择和丢弃边后的图 AG如图3所示。

通过构建图 AG，可以在代理之间分配段，从而最小化总效用值。

3.6 协调

协调阶段是控制代理以完成整体任务的过程。为了通过团队执行物体运输，每个机器人必须按给定顺序并以协调的方式执行其任务。

使用前述算法协调代理并运输一组物体的所提出方法在图5中描述，并且可以分为以下步骤：（i）针对环境中的所有物体，创建一个尚未运输的物体列表；（ii）如果该列表非空，则任意选择其中一个物体，如果为空，则执行完成；（iii）执行代理的规划阶段；（iv）计算所有计划的成本，并进行任务分配，以选择最优的代理来运输该物体；（v）协调过程将物体运送至其最终位置。

示意图5

在开发此方法时考虑的一个假设是，同一时间只有一个代理可以操纵一个物体，因此在任何给定时间仅有一个代理被授权执行任务。授权控制通过机器人之间共享的令牌 τ ∈ TO的交换来实现。令牌 τ具有类型为tmi ∈ TM的属性，该属性表示允许的移动类型。

如第3.4节所述，系统中的每个任务代表一个计划，必须覆盖该计划以执行运输。在执行控制机制之前，集合TO被填入数量相等的令牌 τ类型为<运输>和令牌 τ类型为<预运输>，数量均为 e，然后每个代理执行算法6。

仅创建一个类型为的token会限制执行该类型计划的代理数量，因为物体一次只能由一个代理处理。为了加快整个过程，负责后续段的代理会收到一个类型为的token，以便它们可以执行准备步骤，然后等待当前正在执行类型为计划的代理。

使用上述方法，代理能够以有序的方式并在达成共识的情况下完成任务，同时利用运输前的步骤来缩短整个过程的时间。该任务执行阶段通过代理之间的信息交换来实现

算法6. 协调机制 (S)
1: 对所有 si ∈ S执行
2: ri ← 获取机器人(si)
3: 给予令牌(<预运输>, TO, ri)
4: 如果是当前机器人(ri)则
5: give token(<运输>, TO, ri)
6: 执行任务(ri)
7: 检索令牌(<预运输>, TO, ri)
8: 检索令牌(<运输>, TO, ri)
9: else
10: 执行任务(ri)
11: 检索令牌(<预运输>, TO, ri)
12: 重复
13: 等待()
14: until 拥有传输令牌(TO)
15: 结束如果
16: 结束循环

代理，例如它们动作的当前状态以及它们之间交换的token。

4 实验

本节展示了采用本文所述方法进行的实验及其获得的结果。实验分为两类：（i）定性评估，包括涉及多个机器人的仿真；（ii）演示实验，即使用真实代理进行的实验。

4.1 仿真

所提出的方法能够生成不同类型的计划以完成运输任务。通过使用效用函数并改变常数 α的值，表明该方法具有灵活性，能够满足特定需求，例如在执行任务时尽量减少总时间或消耗的能量。

最初，我们展示了一个实验，说明了该方法在使用不同 α值时的行为。图 6显示了实验中使用的工作空间以及该常数每种变化下的生成的路径。表1列出了每次实验中用于对时间与能量等各特征进行权重设置的数值。可以看出，该方法适用于不同类型的车辆，并且可以考虑特定的任务需求。

可以观察到，当 α取不同值时，生成的路径完全不同。当权重倾向于时间方面时，路径为空中路径，因为这是最快的方式。然而，当以能量消耗为优化目标时，整个运输过程均使用地面代理，因其能量消耗较低。

图6. 根据不同 α值获得的不同路径。有两个车辆可用，一个地面车辆（圆形，红色路径）和一个空中车辆（三角形，蓝色路径）。

最后，在取中等值的情况下，使用两个代理来运输该物体。

下一个实验旨在实证评估当可用机器人数量增加时该方法的渐近行为。该框架使用Python实现，所有实验均在一台配备 Intel Core i7 2.4 GHz 处理器、8 GB 内存和 Ubuntu 14.04 64位操作系统的计算机上进行。

图7显示，该方法随着机器人数量的增加呈现出线性行为。还可以观察到，随着初始和最终构型之间的距离变远，计算时间也随之增加。考虑到所有代理都必须计算自身运输物体的路径，然后在任务分配阶段考虑所有路径，这种行为是预期之中的。

实验	α	时间	能量	图。
1	1	1	0	6(b)
2	0	0	1	6(c)
3	0.5	0.5	0.5	6(d)

表1. 实验中使用不同权重常数。

4.2 真实实验

在此，我们展示了一个概念验证实验，以证明两个主要方面：（i）我们方法的实时执行，以及（ii）在简化的实际条件下规划路径的可行性。

实验在面积约为 2× 2 m的桌面上进行，以确保移动机器人拥有平坦的表面。在此情况下，通过使用跟踪系统观察场景中每个物品上的标记码并向系统报告，从而简化了定位过程，并建立了全局定位结构。实验中所用障碍物的位置事先在实验地图上配置并告知各代理。

任务是使用一个由三台地面机器人（e‐Puck平台²）组成的团队，在包含任意数量障碍物的工作空间中运输一个可忽略重量的物体。图8展示了机器人和物体的初始和最终构型。

图8. 使用三个差动地面机器人运输一个物体的真实实验。所有机器人共同协作完成物体运输，以满足系统需求。

图9. 由三个真实代理组成的团队对一个物体的运输示例。在完成物体路径规划后，所有代理评估每个段的最优选择，从而实现所有机器人的分配，以完成物体的完整运输。

可以看出，在运输任务中使用了所有三个代理，每个代理分别执行物体总路径的一部分。开始时，选择代理1启动运输，而其他代理则移动并等待轮到它们执行操作。一旦物体沿第一段路径移动（S₁ ‐ 图9(c)），代理2便成为负责代理，并将物体运送至第二段路径的末端（S₂ ‐ 图9(e)），然后将物体传递给代理3，由其通过S₃段将物体运送到底最终位置（图9(g)）。这表明系统能够利用可用资源来优化任务的执行结果。