Understanding Diffusion Models: A Unified Perspective翻译和公式补充解读

“Understanding Diffusion Models: A Unified Perspective”是一篇写的非常好的扩散模型DDPM数学原理解读文章，这里翻译了一遍，对于一些细节补充记录一下，方便对照原文更好的理解。

这篇文章作者是Calvin Luo，来自Google Research的Brain Team，详细介绍了生成模型（Generative Models）的背景知识，包括证据下界（Evidence Lower Bound, ELBO）、变分自编码器（Variational Autoencoders, VAEs）以及层级变分自编码器（Hierarchical Variational Autoencoders, HVAEs）等概念。接着，深入探讨了变分扩散模型（Variational Diffusion Models）的学习、噪声参数的学习，以及三种等效的解释。此外，还讨论了基于分数的生成模型（Score-based Generative Models），以及分类器引导（Classifier Guidance）和无分类器引导（Classifier-Free Guidance）等技术。

1.引言：生成模型

生成模型的目标是从观测到的样本$x$中学习其真实的数据分布$p(x)$。一旦学习完成，我们可以随意从近似模型中生成新的样本。此外，在某些场景下，我们还能够使用学习到的模型来评估观测或采样数据的可能性。

当前文献中有几种主流的方向，我们仅在高层次上简要介绍。生成对抗网络（GANs）以对抗方式学习复杂分布的采样过程。另一类被称为“基于似然”的生成模型，寻求学习一个模型，为观测数据样本分配高似然。这包括自回归模型、归一化流和变分自编码器（VAEs）。另一种类似的方法是能量建模，其中分布被学习为任意灵活的能量函数，然后进行归一化。

基于分数的生成模型与之高度相关；它们不是学习建模能量函数本身，而是将能量模型的分数学习为神经网络。在这项工作中，我们探索并回顾了扩散模型，正如我们将展示的，它们既有基于似然的解释，也有基于分数的解释。我们尽可能详细地展示了这些模型背后的数学，目的是让任何人都能够理解扩散模型是什么以及它们的工作原理。

2.背景：ELBO、VAE和层级VAE

对于许多模态，我们可以将我们观察到的数据视为由相关但不可见的潜在变量表示或生成，我们可以将这个随机变量表示为z。表达这个想法的最佳直觉是通过柏拉图的洞穴寓言。在寓言中，一群人一生都被锁在一个洞穴里，只能看到前方墙上投下的二维影子，这些影子是由火前经过的不可见三维物体产生的。对于这些人来说，他们观察到的一切都是由他们永远无法看到的高维抽象概念决定的。

类似地，我们在现实世界中遇到的对象也可能是由某些更高层次的表示生成的；例如，这些表示可能封装了颜色、大小、形状等抽象属性。然后，我们观察到的可以被解释为这些抽象概念的三维投影或实例化，就像洞穴人观察到的是三维物体的二维投影一样。虽然洞穴人永远看不到（甚至完全理解不了）隐藏的物体，他们仍然可以推理并推断出它们的存在；同样，我们可以近似潜在表示，描述我们观察到的数据。

柏拉图的洞穴寓言阐述了潜在变量作为可能不可观测的表征，这些表征决定了观测结果。然而，这个类比的一个警告是，在生成建模中，我们通常寻求学习的是低维度的潜在表征，而不是高维度的。这是因为尝试学习比观测结果更高维度的表征，如果没有强有力的先验知识，将是一种徒劳的努力。另一方面，学习低维度的潜在表征也可以被视为一种压缩形式，并且可能揭示出描述观测结果的语义上有意义的结构。

2.1证据下界（Evidence Lower Bound）

数学上，我们可以想象潜在变量和我们观察到的数据由联合分布$p(x,z)$建模。回想一下，称为“基于似然”的生成建模方法是学习一个模型来最大化所有观测到的x的似然$p(x)$。我们可以以两种方式操纵这个联合分布来恢复我们纯粹观测数据的似然$p(x)$；我们可以显式地边缘化潜在变量$z$

$p(\mathbf{x})=\int p(\mathbf{x},\mathbf{z})d\mathbf{z}$ (1)

或者，我们也可以求助于概率的链式法则：

$p(\mathbf{x})=\frac{p(\mathbf{x},\mathbf{z})}{p(\mathbf{z}|\mathbf{x})}$ （2）

直接计算和最大化似然$p(x)$是困难的，因为它要么涉及在方程1中积分出所有潜在变量$z$，这对于复杂模型来说是不可解的，或者它涉及访问真实潜在编码器$p(z|x)$的访问。然而，使用这两个方程，我们可以推导出一个称为证据下界（ELBO）的项，顾名思义，它是证据的下界。在这种情况下，证据被量化为观测数据的对数似然。然后，最大化ELBO成为了优化潜在变量模型的代理目标；在最好的情况下，当ELBO被强有力地参数化并完美优化时，它变得与证据完全等价。ELBO的方程是：

${\mathbb{E}}_{q_{\varphi }(\mathbf{z}|\mathbf{x})}\left[\log \frac{p(\mathbf{x},\mathbf{z})}{q_{\varphi }(\mathbf{z}|\mathbf{x})}\right]$ (3)

为了使与证据的关系明确，我们可以数学上写出：

$\log p(\mathbf{x})\ge {\mathbb{E}}_{q_{\varphi }(\mathbf{z}|\mathbf{x})}\left[\log \frac{p(\mathbf{x},\mathbf{z})}{q_{\varphi }(\mathbf{z}|\mathbf{x})}\right]$ (4)

这里，$q_{\mathbf{\varphi }}(\mathbf{z}|\mathbf{x})$是一个灵活的近似变分分布，其参数$\phi $我们寻求优化。直观地说，它可以被认为是一个可学习的参数化模型，用于估计给定观测$x$的潜在变量的真实分布；换句话说，它寻求近似真实的后验$p(z|x)$。当我们通过调整参数$\phi $​来增加下界以最大化ELBO时，我们获得了可以用来建模真实数据分布并从中采样的组件，从而学习了一个生成模型。现在，让我们尝试更深入地了解为什么我们希望最大化ELBO。

变分分布：变分分布是变分推断中用于近似复杂后验分布的简化模型。它通过优化一个参数化的分布族来最好地捕捉原始分布的关键特征，通常选择易于计算且足够灵活的分布作为变分分布族，并通过最小化与真实后验分布的KL散度来调整参数。这种方法使得在计算上不可行的复杂概率分布推断变得可行。

我们首先使用公式 1 推导 ELBO：

(6)->(7)解释:将对随机变量的积分转换为对其概率分布的期望值，意味着我们不是直接计算随机变量在所有可能取值上的积分，而是计算这个随机变量按照其概率分布取值时的平均值。这种转换是基于期望值的定义，即一个随机变量的期望值是它所有可能取值的概率加权和。具体来说，假设我们有一个随机变量 $X$ 和一个概率分布 $p(x)$，那么 $X$的期望值 $E[X]$定义为：$E[X]=\int xp(x)dx$。在变分推断中，由于直接计算(5)这个积分可能非常复杂，因此利用期望的性质来简化问题。期望的性质允许我们将对随机变量的积分转换为对其概率分布的期望值。

(7)->(8)解释：Jensen不等式是一个凸函数性质的结果，对于任意凸函数 $f$和概率分布 $P$，以下不等式成立：$\log {\mathbb{E}}_P[X]\ge {\mathbb{E}}_P[\log X]$

在这个推导过程中，我们通过应用詹森不等式直接得到了我们的下界。然而，这并没有给我们提供太多有关背后实际发生的事情的有用信息；关键的是，这个证明并没有给出为什么ELBO实际上是证据的一个下界的直觉，因为詹森不等式把它轻描淡写了。此外，仅仅知道ELBO是数据的一个真正的下界，并不足以告诉我们为什么我们想要将其最大化作为一个目标。为了更好地理解证据和ELBO之间的关系，让我们再次进行推导，这次使用方程2。

(15)解释：KL散度也称为相对熵（Relative Entropy），是衡量两个概率分布差异的一种方法。它是两个概率分布 $P$和 $Q$之间的非对称距离度量，定义为：$D_{KL}(P||Q)={\sum }_{x}P(x)\log \left(\frac{P(x)}{Q(x)}\right)$，其中，$P$ 是数据的真实分布，而 $Q$ 是模型或估计分布。KL散度的值总是非负的，当且仅当 $P$和 $Q$ 完全相同时，KL散度为零。

从这个推导中，我们可以清楚地从方程15观察到，证据等于ELBO加上近似后验分布$q_{\mathbf{\varphi }}(\mathbf{z}|x)$和真实后验分布 $p(\mathbf{z}|\mathbf{x})$之间的KL散度。实际上，正是这个KL散度项在第一次推导的方程8中被詹森不等式神奇地消除了。理解这个项是理解ELBO与证据之间的关键，以及为什么优化ELBO是一个合适的目标的关键。

首先，我们现在知道为什么 ELBO 确实是一个下界：证据和 ELBO 之间的差异是严格非负 KL 项，因此 ELBO 的值永远不会超过证据。

图 1：以图形方式表示的变分自动编码器。这里，编码器 $q(z|x)$ 定义了观测值 $x$ 的潜在变量 $z$ 的分布，并且 $p(x|z)$ 将潜在变量解码为观测值。

其次，我们探讨为什么我们要寻求最大化ELBO。在我们引入了想要建模的潜在变量 $z$之后，我们的目标是学习描述我们观测数据的潜在结构。换句话说，我们想要优化变分后验$q_{\varphi }(\mathbf{z}|\mathbf{x})$的参数，以便它能精确匹配真实的后验分布$p(\mathbf{z}|\mathbf{x})$，这是通过最小化KL散度（理想情况下为零）来实现的。不幸的是，直接最小化KL散度项是非常困难的，因为我们没有真实分布 $p(\mathbf{z}|\mathbf{x})$ 的访问权限。

然而，请注意，在方程15的左侧，我们的数据的似然性（我们的证据项 $\log p(\mathbf{x})$）对于 $\varphi$来说始终是一个常数，因为它是通过从联合分布 $p(\mathbf{x},\mathbf{z})$中边缘化所有潜在变量 $\mathbf{z}$ 来计算的，而且它不依赖于 $\varphi$。由于ELBO和KL散度项的总和是一个常数，任何对ELBO项关于 $\varphi$ 的最大化必然会导致KL散度项的同等最小化。

因此，ELBO可以被最大化，作为学习如何完美建模真实潜在后验分布的一个代理目标；我们对ELBO的优化越多，我们的近似后验就越接近真实的后验。此外，一旦模型训练完成，ELBO还可以用于估计观测到的或生成的数据的似然性，因为它被训练来近似模型的证据 $\log p(\mathbf{x})$。

2.2 变分自动编码器(Variational Autoencoders)

在变分自编码器（VAE）的默认公式中，我们直接最大化ELBO。这种方法是变分的，因为我们在由$\varphi$参数化的一系列潜在后验分布中优化以找到最佳的 $q_{\varphi }(\mathbf{z}|\mathbf{x})$。它被称为自编码器，因为它让人想起了传统的自编码器模型，在这种模型中，输入数据经过一个中间的瓶颈表示步骤后被训练来预测自身。为了明确这种联系，让我们进一步剖析ELBO项：

在这种情况下，我们学习了一个中间瓶颈分布 $q_{\varphi }(z|x)$，它可以被视为一个编码器；它将输入转换为可能的潜在变量的分布。同时，我们学习了一个确定性函数 $p_{\theta }(x|z)$来将给定的潜在向量 $z$ 转换成观测值 $x$，这可以被解释为一个解码器。

方程19中的两个项各自有直观的描述：第一项衡量了解码器从我们的变化分布中重构的可能性；这确保了学习到的分布是模拟有效的潜在变量，原始数据可以从中再生。第二项衡量了学习到的变化分布与对潜在变量持有的先验信念的相似度。最小化这个项鼓励编码器实际学习一个分布，而不是塌陷成一个狄拉克$\delta$函数。

因此，最大化ELBO（证据下界）相当于最大化其第一项并最小化其第二项。

变分自编码器（VAE）的一个决定性特征是它如何联合地对参数$\varphi$和$\theta$进行ELBO（证据下界）优化。VAE的编码器通常被选择来对角线协方差矩阵的多变量高斯分布进行建模，而先验通常被选择为标准的多变量高斯分布：

然后，ELBO中的KL散度项可以被解析地计算出来，重构项可以使用蒙特卡洛估计来近似。我们的目标随后可以被重写为：

(22)解释：为了优化这个目标函数，我们通常需要计算它的梯度，并使用反向传播算法进行参数更新。然而，直接计算ELBO的期望项可能涉及到对随机变量的期望，这在计算上是不可行的。为了解决这个问题，我们可以使用蒙特卡洛近似来估计期望。从 $q_{\varphi }(z|x)$中采样多个潜在变量 { z(l)}l=1L\{z^{(l)}\}_{l=1}^{L}{ z(l)}l=1L​，然后计算这些样本的平均值作为期望的近似。这样，原始的ELBO可以被近似为：$\approx \frac{1}{L}{\sum }_{l=1}^L\left[\log p_{\theta }(x|z^{(l)})-D_{\mathrm{KL}}(q_{\varphi }(z|x)\parallel p(z))\right]$

需要注意的是，这个近似假设了 $q_{\varphi }(z|x)$可以被重参数化，这是使用蒙特卡洛方法的前提。对于多变量高斯分布，由于其闭合形式的性质，可以通过改变随机变量的表示来实现重参数化，从而使得这个近似成立。

在这个设置中，潜在变量{ z(l)}l=1L\{z^{(l)}\}_{l=1}^{L}{ z(l)}l=1L​从编码器分布 $q_{\varphi }(z|x)$中采样，对于数据集中的每个观测值 $x$ 都是如此。然而，在这个默认设置中出现了一个问题：每次计算损失函数时所使用的每个$z^{(l)}$都是通过一个随机采样过程生成的，这个过程通常是不可微的。 幸运的是，当 $q_{\varphi }(z|x)$被设计为模拟某些特定分布时，包括多变量高斯分布，这个问题可以通过重参数化技巧来解决。重参数化技巧允许我们对随机采样过程进行变换，使其成为一个可微分的操作，从而可以使用标准的反向传播算法来优化模型参数。这样，即使原始的采样过程是不可微的，我们也可以通过这种技巧来有效地训练VAE模型。

重参数化技巧将随机变量改写为一个噪声变量的确定性函数，这允许通过梯度下降法优化非随机项。例如，来自正态分布 $x\sim \mathcal{N}(x;\mu ,{\sigma }^2)$ 的样本，其中 $\mu$是任意均值，${\sigma }^2$ 是方差，可以被改写为：

在这里，$ϵ$是一个标准正态分布 $ϵ\sim \mathcal{N}(0,1)$的随机变量，而 $f(ϵ)$是一个确定性函数，它依赖于 $ϵ$但不是随机的。通过这种方式，原始的随机采样过程 $x$被转换成了一个参数化的确定性过程，其中 $\mu$ 和 $\sigma$成为了可优化的参数。这种改写的关键之处在于，它使得 $x$ 的分布依赖于 $\mu$和 $\sigma$，而这两个参数可以通过梯度下降法进行优化。这是因为 $f(ϵ)$是 $ϵ$的确定性函数，所以 $x$关于 $\mu$ 和 $\sigma$的导数可以被计算出来，从而可以使用反向传播算法来更新这些参数。在变分自编码器（VAE）的上下文中，这种技巧特别有用，因为它允许我们对编码器 $q_{\varphi }(z|x)$和解码器 $p_{\theta }(x|z)$的参数进行优化，即使原始的采样过程是不可微分的。通过这种方式，我们可以有效地训练VAE模型，同时保持其生成的数据与真实数据的相似性，并且能够通过调整模型参数来控制生成数据的多样性。

解释：重参数化技巧

重参数化技巧是机器学习和深度学习中用于处理随机梯度问题的一种方法。在许多模型中，特别是在生成模型如变分自编码器（VAE）中，我们经常需要从概率分布中采样，而这些采样操作本身是随机的，不可导的。这就意味着我们不能直接通过这些随机采样来计算梯度，并用它们来更新模型参数。

为了解决这个问题，重参数化技巧通过引入一个新的随机变量，并将其作为一个噪声变量来重新表达原始的随机采样。这个新的表达式是原始随机变量的一个确定性函数，这意味着它完全依赖于模型参数和一个新的独立的随机变量。这样，我们就可以通过这个新的随机变量来计算原始随机变量的期望值，而这个期望值是可导的，因为它不再依赖于模型参数的随机选择。具体来说，假设我们有一个随机变量 $Z$，它是通过从某个分布 $P(Z)$中采样得到的。在没有重参数化技巧的情况下，我们不能直接对 $Z$进行梯度下降优化。但是，如果我们能够找到一种方法，使得 $Z$可以被表达为一个确定性函数 $g$和一个独立的随机变量 $ϵ$的组合，即 $Z=g(ϵ;\theta )$，其中 $\theta$ 是模型参数，那么我们就可以使用 $ϵ$来计算 $Z$的期望值，并通过 $ϵ$的分布来计算梯度。这种方法的关键优势在于，尽管 $Z$本身是随机的，但 $g(ϵ;\theta )$ 是确定性的，并且可以通过 $ϵ$来计算梯度。因此，我们可以使用标准的梯度下降算法来优化模型参数 $\theta$，即使整个表达式涉及到随机变量。

在VAE的情况下，重参数化技巧允许我们将编码器输出的随机潜在变量 $Z$其他 重写为一个关于模型参数 $\varphi$的确定性函数，同时依赖于一个独立的随机变量。这样，我们就可以通过梯度下降来优化编码器和解码器的参数，同时保持生成的数据与真实数据的相似性。

换句话说，任意的高斯分布可以被解释为标准高斯分布（其中 $ϵ$是一个样本），其均值从零移动到目标均值 $\mu$ 通过加法实现，其方差通过目标方差 ${\sigma }^2$ 进行伸缩。因此，通过重参数化技巧，从任意高斯分布中采样可以通过从标准高斯分布中采样，将结果按目标标准差进行缩放，并通过目标均值进行偏移来实现。

在变分自编码器（VAE）中，每个潜在变量 $z$因此可以被计算为输入 $x$和辅助噪声变量 $ϵ$的确定性函数。这个过程通常涉及以下步骤：

在这个重参数化的 $z$版本下，可以计算相对于 $\varphi$的梯度，以期望优化 ${\mu }_{\varphi }$和 ${\sigma }_{\varphi }$。因此，变分自编码器（VAE）利用重参数化技巧和蒙特卡洛估计来联合优化 $\varphi$和 $\theta$上的证据下界（ELBO）。其中，符号 $\odot$ 表示逐元素乘积。

训练 VAE 后，可以通过直接从潜在空间 $p(z)$ 采样然后通过解码器运行来生成新数据。当 $z$ 的维度小于输入 $x$ 的维度时，变分自动编码器特别有趣，因为我们可能会学习紧凑、有用的表示。此外，当学习到语义上有意义的潜在空间时，可以在将潜在向量传递到解码器之前对其进行编辑，以更精确地控制生成的数据。

2.3 分层变分自动编码器（Hierarchical Variational Autoencoders）

分层变分自动编码器 (HVAE) 是 VAE 的推广，可扩展到潜在变量的多个层次结构。根据公式，潜在变量本身被解释为从其他更高级别、更抽象的潜在变量生成。直观上，就像我们将三维观察对象视为从更高层次的抽象潜在对象生成一样，柏拉图洞穴中的人们将三维对象视为生成二维观察的潜在对象。因此，从柏拉图的洞穴居民的角度来看，他们的观察可以被视为由深度为二（或更多）的潜在层次结构建模。

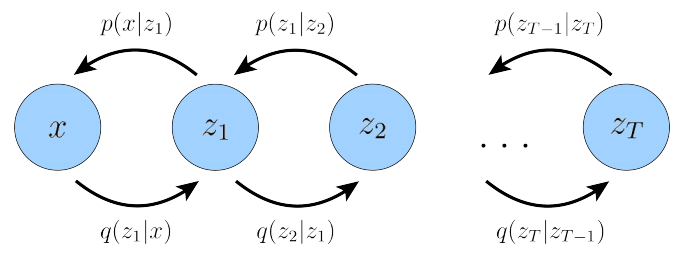
图 2：具有 T 个分层潜在变量的马尔可夫分层变分自动编码器。生成过程被建模为马尔可夫链，其中每个潜在 $z_t$ 仅从前一个潜在 $z_{t+1}$ 生成。

与具有T层层次结构的一般分层变分自编码器（HVAE）不同，在一般HVAE中，每个潜在变量都被允许基于所有先前的潜在变量进行条件化；在本研究中，我们关注的是一个特殊情况，我们称之为马尔可夫分层变分自编码器（MHVAE）。在MHVAE中，生成过程是一个马尔可夫链；也就是说，层次结构中的每个转换都是马尔可夫的，其中解码每个潜在变量 ztz_t