菜鸟学Python | 四大经典算法之一：贪心算法思想

原创于 2025-01-16 17:48:23 发布 · 947 阅读

21 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #python #贪心算法 #深度学习 #人工智能 #优化 #数据分析

深度学习拓展阅读同时被 2 个专栏收录

989 篇文章

订阅专栏

统计学

29 篇文章

订阅专栏

本文来源公众号“菜鸟学Python”，仅用于学术分享，侵权删，干货满满。

原文链接：https://mp.weixin.qq.com/s/YhzC8deUc-PWxFEy3b-nEg

所谓贪心，就是一直追求最好的选择。由于算法执行时重点关注的区域是本层执行空间，即本层循环或作用域，所以贪心算法的侧重点也是本层执行空间。因为其他层空间的参数无法直接涉及，所以贪心算法就是在本层空间或者本次执行中追求最优的算法结果。所以，贪心思想追求的是局部最优，并且是每一步都追求局部最优。但是本次局部最优可能会对上一次的局部最优造成影响，因此贪心思想可能无法获取最优解。但是，这对一些无最优解的问题又是很适合的。

贪心的原理

贪心算法的核心可以理解为:每次只追求局部最优，不兼顾或不考虑全局最优。贪心算法的设计直截了当，只看当前，不看整体或后来。在贪心思想中,“贪心”的是本次的运算能够获取最优解，而不用顾虑对全局造成的因此该算法执行时简单、直接、效率高，但是容易陷入局部最优的困境中。

因此在选择贪心算法时需要考虑效率与其对全局最优的影响。一般在效率比获取全局最优解更加重要时采用贪心算法。假设某个算法共有 12 个可选的执行步骤，在图 5.11 中用 12 个矩形来表示。这 12矩形的宽度相等，长度代表矩形的执行效果，长度越长，则执行效果越好。

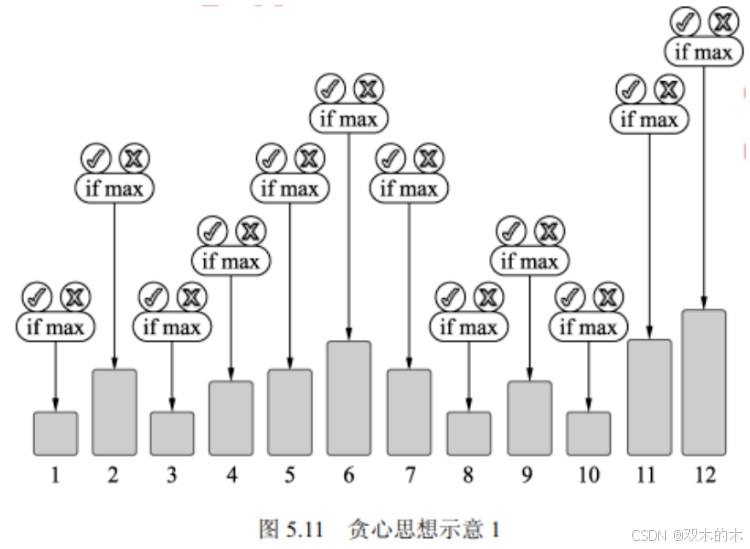
现在要求在有限的 N次执行内执行完算法，每次执行只能选择有限的M个执行步骤。要求最后获得的算法执行效果最好。

因为执行次数 N 与执行步骤 M 是有限的，所以最终能够选择的有效执行次数只有NXM 次。要求算法执行效果最好，那么每次选择的执行步骤的效果最好，即对应的矩形长度最长。

因此，每次选择执行步骤时，都要在剩余的可选步骤中选择最大的矩形。

因此尽量获取当前步骤的最大执行效果，就是贪心算法的特征。

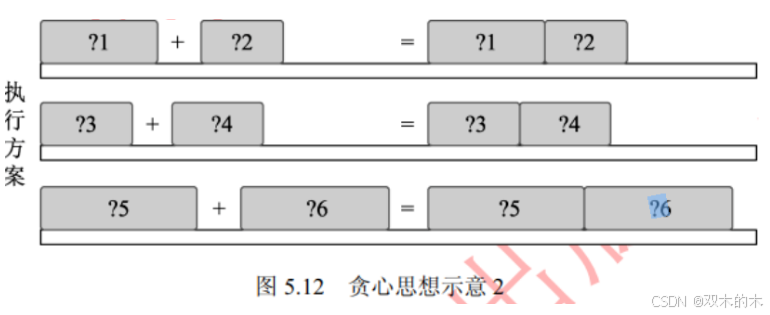
假设当前有3种执行方案可选，如图5.12所示。每种方案有两个执行步骤，用矩形表示。

现在要求当前执行的效果最好，显然要选择执行步骤相加效果最好的方案，即矩形长度最长的两个矩形。

贪心算法实例

下面进一步拓展上一小节的实例，详细阐述贪心算法的设计原理与实施过程首先进一步量化如图 5.11 所示的实例，要求在有限的执行次数(N3)内执行完算法，每次执行只能选择两个执行步骤(M-2)。要求最后获得的算法执行效果最好。

如图 5.13 所示,为了方便量化,将图 5.11 中代表执行步骤效果的矩形长度使用数字量化标注，数字越大，说明执行效果越好。

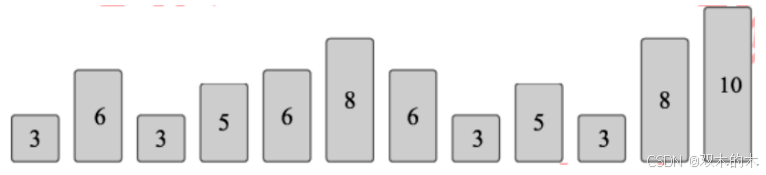
图5.13 贪心算法实用实例1

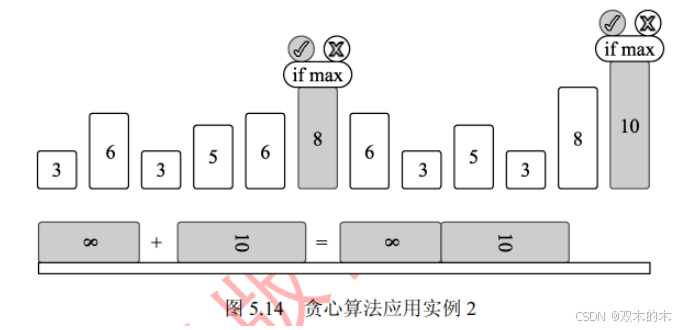
然后开始第1次执行,如图 5.14所示,选取当前可选执行步骤中执行效果最好的两步,即长度最长的两个矩形8和 10。

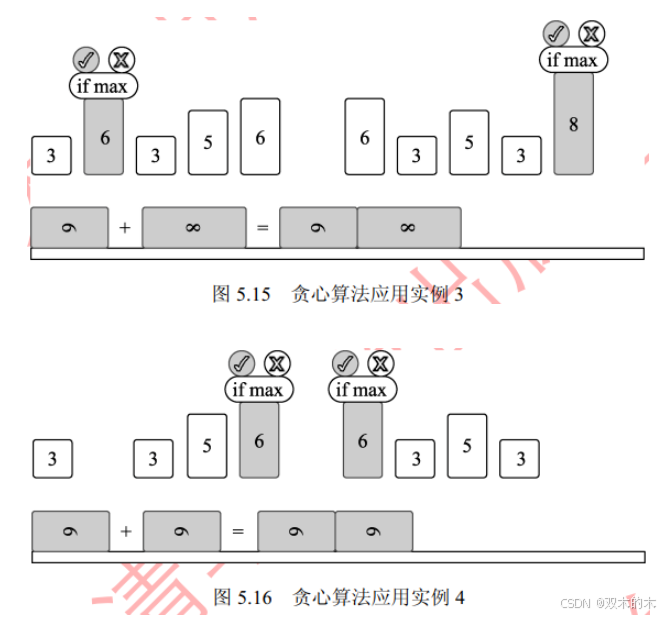
然后开始执行第2次,如图 5.15 所示,选取当前可选执行步骤中执行效果最好的两步,即长度最长的两个矩形6和8。

然后开始执行第3次,如图 5.16所示,选取当前可选执行步骤中执行效果最好的两步,即长度最长的两个矩形6和 6。

最终的执行效果如图 5.17 所示。

由于每次执行时选择的都是两个执行步骤中的最优效果，即长度最长的矩形，假设执行效果可以相加，经过3次执行(6个执行步骤)后，所获得的执行效果应该是最好的，即矩形相加的长度最长。

下面结合上述实例与分析，通过具体的代码，来理解贪心算法的原理与实施过程。代码实现:

# 贪心思想
def greedy():
    ops = [3, 6, 3, 5, 6, 8, 6, 3, 5, 3, 8, 10]
    print('所有可选的执行步骤的效果列表为' + str(ops))
    op_max_len = []

    for i in range(3):
        print('第' + str(i + 1) + '次执行:')
        max_1 = max(ops)
        ops = ops[:ops.index(max_1)] + ops[ops.index(max_1) + 1:]
        max_2 = max(ops)
        ops = ops[:ops.index(max_2)] + ops[ops.index(max_2) + 1:]
        print('当前最优的2个执行步骤的矩形长度为' + str(max_1) + '和' + str(max_2))
        op_max_len.append(max_1)
        op_max_len.append(max_2)
        print(f'最优执行步骤的矩形长度集合为{op_max_len}')

    # 计算最优执行步骤的矩形长度之和
    all_len = 0
    for it in op_max_len:
        all_len += it
    print(f'最优执行步骤的矩形长度之和为{all_len}')

# 测试
greedy()

输出：

所有可选的执行步骤的效果列表为[3，6，3，5，6，8，6，3，5，3，8，10]
第 1次执行:
当前最优的2个执行步骤的矩形长度为:10和8
第 2 次执行:
当前最优的2个执行步骤的矩形长度为:8和6
第 3次执行:
当前最优的2个执行步骤的矩形长度为:6和6
最优执行步骤的矩形长度集合为op_maxlen =[10，8，8，6，6，6]
最优执行步骤的矩形长度之和为 all len = 44

THE END !

文章结束，感谢阅读。您的点赞，收藏，评论是我继续更新的动力。大家有推荐的公众号可以评论区留言，共同学习，一起进步。